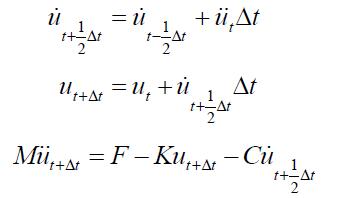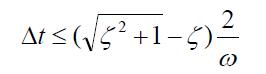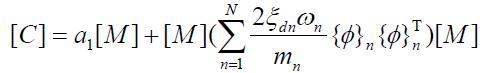Case 1 Scordelis-Lo roof problem

The Scordelis-Lo roof problem is shown in Figure 1. The cylindrical panel is loaded vertically with a uniform self-weight of g = 90. Both edges are fixed. Due to the symmetry, only one quarter of the panel is modeled. Three meshes are used in this analysis, as shown in Table 1. The vertical deflection of Point A is recorded. The exact solution of 0.3024 provided by MacNeal and Harder is used as a reference. The results are shown in Table 1.

Figure 1 Scordelis-Lo roof problem

Table 1 Results of Scordelis-Lo roof problem

Case 2 Twisted beam problem

The twisted beam problem is shown in Figure 2. A concentrated load is applied at the free end in the in-plane (P) and out-of-plane (Q) directions, respectively. A mesh of 2 × 12 is adopted for this problem. Two load cases are analyzed: (1) P = 1, Q = 0; and (2) Q = 1, P = 0. The displacement along the loading direction at the free end is recorded. The exact solutions provided by MacNeal and Harder are used as a reference. The comparison is shown in Table 2.

Figure 2 Twisted beam problem

Table 2 Results comparison for the twisted beam problem

2.     Leap-frog method

Because the central difference method cannot ensure the equations decoupled, which limits the computational speed, the leap-frog method is integrated into OpenSees. The leap-frog method has a simple formula, and can ensure the equations decoupled. However, it should be noted that there must be no zero element among the diagonal elements of the mass matrix when using the leap-frog method. However, some elements in OpenSees have zero inertia for the rotation degree-of-freedoms. Such element should not be used together with the leap-frog method.

The fundamental equations of the leap-frog method are shown as follows:

The critical time step size of the leap-frog method is as follow:

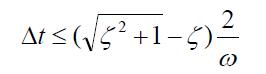
Note that when the leap-frog method is used with Rayleigh damping, the damping ratio of the higher vibration modes is overestimated. Consequently, the critical time step size should be much smaller than that for the implicit method.

3.     Modal damping

The critical time step size of the leap-frog method is controlled by damping ratio. Because the Rayleigh damping model is not suitable for the leap-frog method, we added Modal damping into OpenSees.

We made the modal damping as a subclass of LinearSOE based on the diagonal class because diagonalSOE is suitable for the leap-frog method. More details can be seen in the codes. In addition, in order to get the pointers and data from other modules, many codes are added in some other classes.

The command to use modal damping is shown as follows:

$Dratio is the target damping ratio; $startfreq and $endfreq specify the frequency range to be controlled; $alphaM is the mass proportional coefficient of Rayleigh damping. $alphaM (a₁) is introduced here because we often use modal damping and mass damping together as follow:

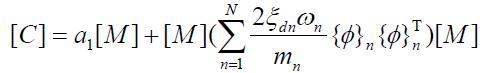
$Dratio is the total damping ratio; Thus, the damping ratio of modal damping  can be calculate by $Dratio and $alphaM.

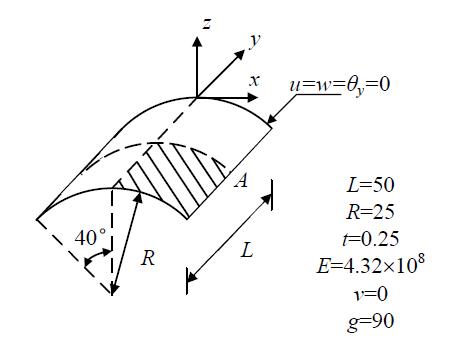
Case 3 Earthquake-induced collapse simulation of a frame structure

Figure 3 shows an eight-story frame structure, with a total height of 31.5 m. There are 3 spans in the x direction, 2 spans in the y direction and each span is 5 m. El-Centro ground motion is used as input in the x direction. More details of the modes can be seen in the Tcl files.

First, when PGA = 510 cm/s², the time history of the top displacement is shown in Figures 4 - 6. Then the PGA is increased to 3500 cm/s² to perform the collapse simulation. The top displacement results are shown in Figure 7. It should be noted that in order to make the leap-frog method work, we added some codes in dispcolumnbeam.cpp to set the moment of inertia equal to the translational mass. The vibration periods of the frame with the moment of inertia have little difference with the original ones.

Figures 4 - 6 illustrate that the mass & modal damping has better accuracy than using the mass damping or modal damping only.

Figure 7 shows that the Newmark method (implicit) encounters numerical problem in convergence, but the leap-frog method can simulate the entire collapse process.

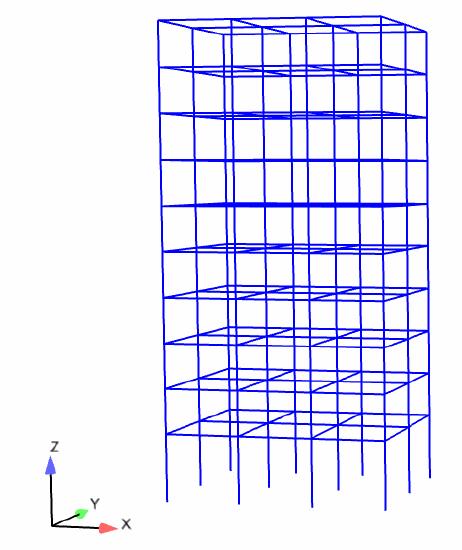
Figure 3 A eight-story frame structure

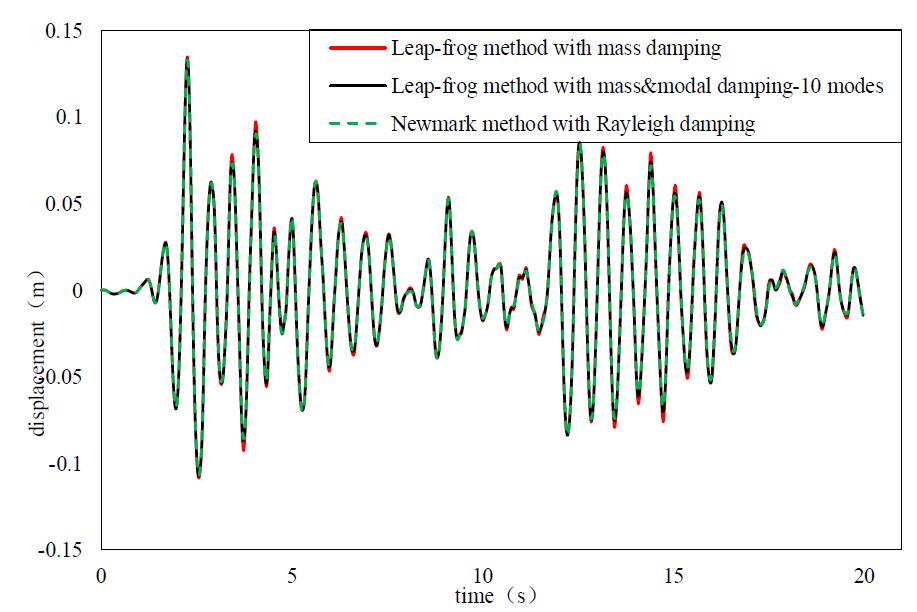
Figure 4 Linear time history responses of the frame structure (PGA=510cm/s²)

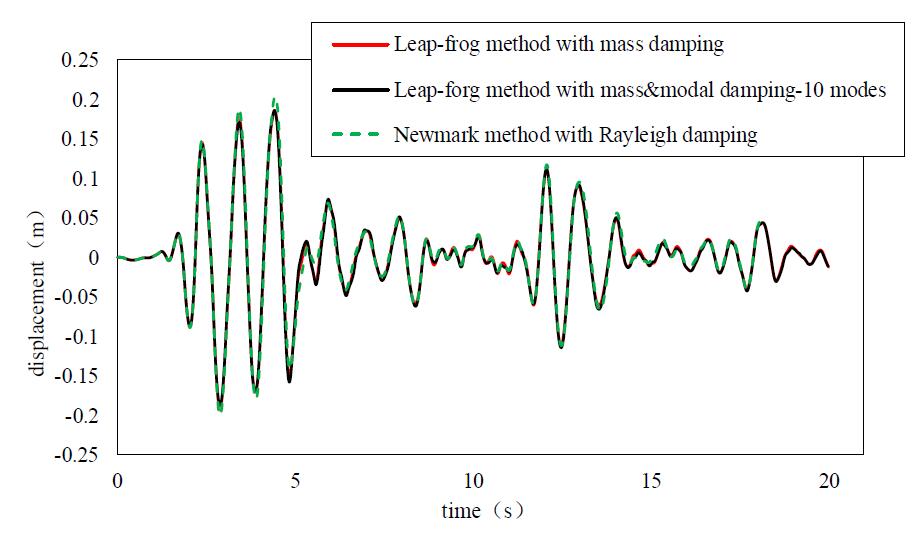
Figure 5 Nonlinear time history response of the frame structure (PGA=510cm/s²)

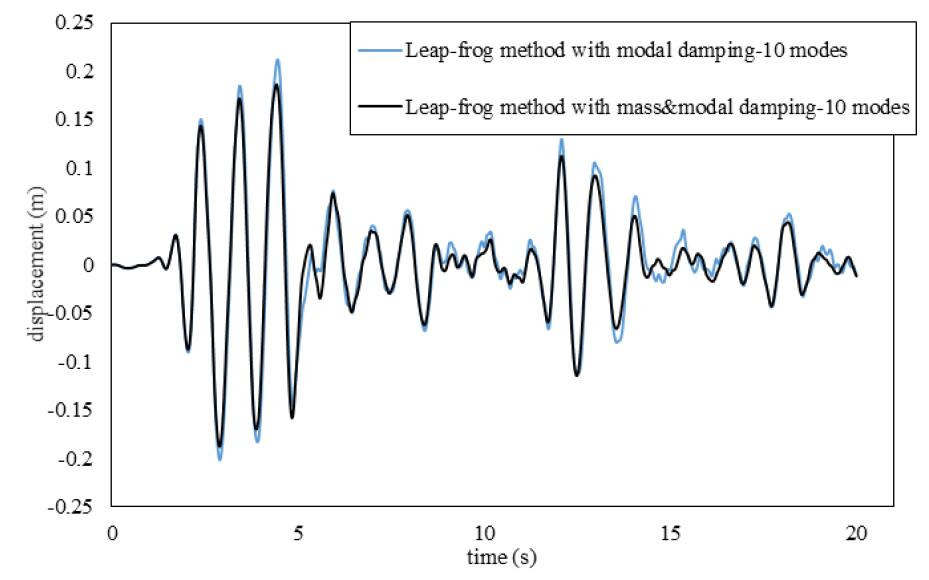
Figure 6 Comparison of the modal damping and the mass & modal damping

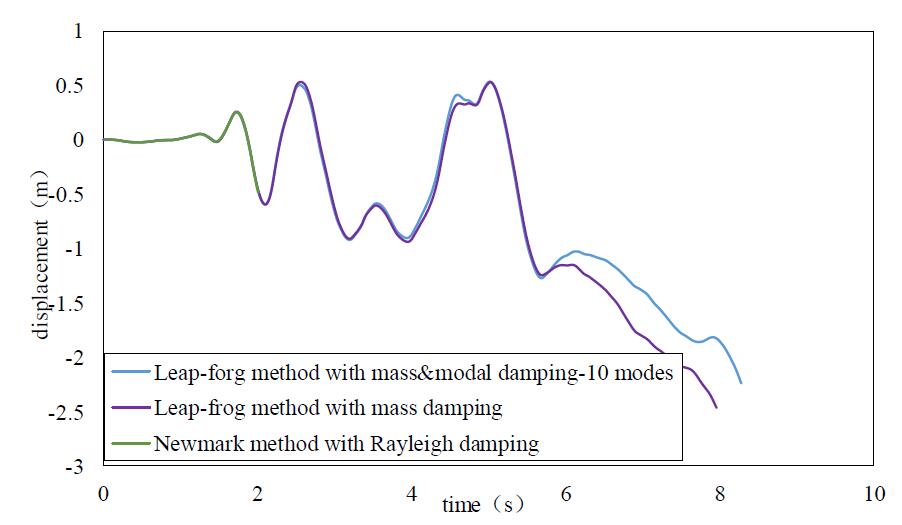
Figure 7 Collapse simulation of the frame structure (PGA=3500cm/s²)