Influence of Structural Parameters to the Seismic Collapse Resistance of RC Frames in 7-degree Seismic Fortification Zone

Dai-yuan Tang, Tsinghua University, China

Xin-zheng Lu, Tsinghua University, China

Lie-ping Ye, Tsinghua University, China

Wei Shi, Tsinghua University, China

Proc. 4th Int. Conf. on Protection of Structures Against Hazards, Oct. 2009, Beijing, China: 331-338.

Download PDF version

Abstract

    Currently in China structural seismic design mostly focuses on design and verification of member strength under minor earthquake. However, during actual earthquakes, structural systems play a more important role in seismic collapse resistance. Therefore, in order to find the influence of structural parameters to the seismic collapse resistance, this paper designs 24 reinforced concrete (RC) frames in 7-degree seismic fortification zone according to the Chinese Seismic Design Code, which have different spans, storey heights and storey numbers. Incremental dynamic analysis (IDA), recommended by ATC-63 Report, is implemented for the frames based on fiber-beam element model to evaluate their seismic collapse resistances. The result shows that structural parameters have a great influence to seismic collapse resistance. The seismic collapse resistance of frames designed according to the Chinese Seismic Design Code with different span has obvious difference. The result could be referred for the further study of seismic collapse resistance.

     Keywords: frame structure, collapse performance, incremental dynamic analysis, nonlinear dynamic analysis, collapse probability

1.    Introduction

Collapse resistance is the most important to ensure the safety of people¡¯s lives and properties. During Wenchuan Earthquake that happened in 2008, although seismic-designed structures shown lighter damages, some structures designed according to the Chinese Code had still been seriously destroyed [1]. In current Chinese Seismic Design Codes, the seismic design is focused on the design and verification of structural elemental strength under minor earthquake, while the performance of whole structures under severe earthquake is mainly ensured by the detail design, which is mostly depended on former earthquake experience and lack of quantitative evaluation [2]. However, the Wenchuan Earthquake showed that frames designed according to the Chinese Seismic Design Code which have different structural system parameters may have a quite different seismic collapse resistance [3], such as the Xuankou School buildings [4]. The structural system parameters show a much more important role for the collapse resistance of frames. Some disproportional collapse may happen in poorly designed structures due to the damage of some weakest members. Thus, it is necessary to evaluate the seismic collapse resistance on structural system level, and then find some quantitative indices that could reflect seismic collapse resistance of structures.

This paper designs 24 reinforced concrete (RC) frames in 7-degree seismic fortification zone according to the Chinese Seismic Design Code [2], which have different spans, storey heights and storey numbers. Incremental dynamic analysis (IDA), recommended by ATC-63 Report, is implemented for the frames to obtain their collapse possibilities under different earthquake intensities. Then, the influence of structural system parameters to the seismic collapse resistance is analyzed.

2.    Collapse possibility analysis based on IDA

2.1 IDA and collapse fragility

The collapse of buildings is a dynamic process. So the pushover analysis, which is widely used in early performance-based earthquake engineering [5] [6] , is not suitable for the collapse analysis. On the contrary, incremental dynamic analysis (IDA), which is proposed by Bertero [7] , analyzes the time-history transient elastic-plastic response of whole structure with step by step increased intensity, which gives a more realistic simulation for the collapse process. However, the results of IDA are highly depended on the selection of ground motion records. A rational set of ground motion records is critical for IDA. So in this research, the 22 far-field ground motion records, which is proposed by ATC-63 Project [8] , together with El-Centro record, which is very familiar for earthquake engineering, are adopted to implement the IDA based collapse analysis. 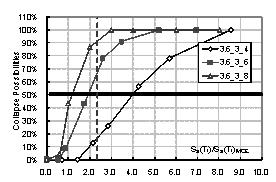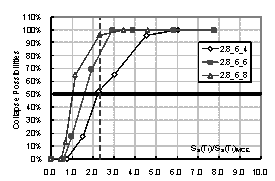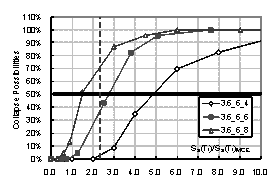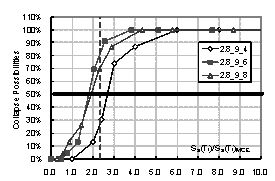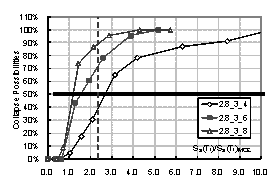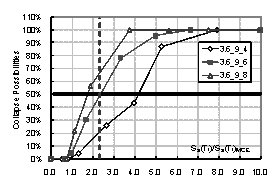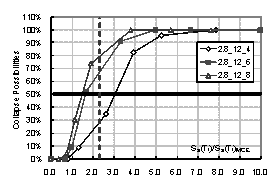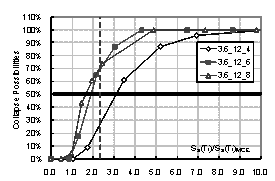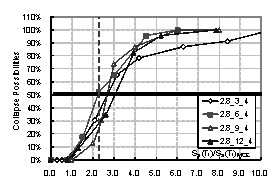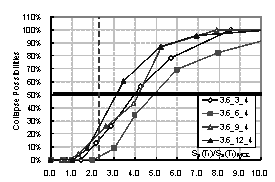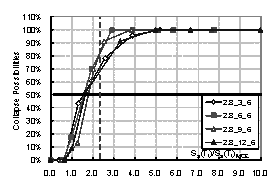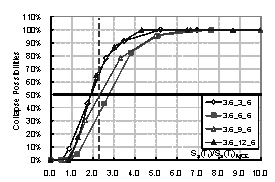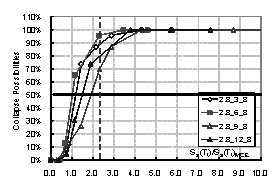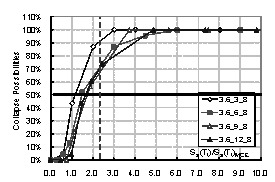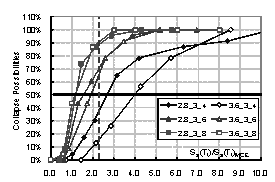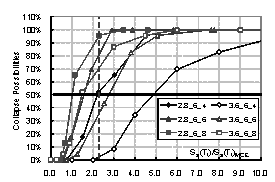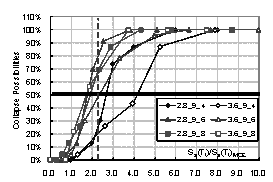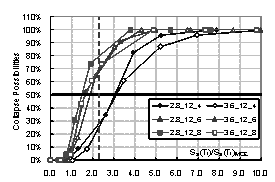If the total number of ground motions are N_total, and under a certain intensity (in this work S_a(T₁), which is the 5% damped spectral acceleration at the structure¡¯s first-mode period, is used to represent the ground motion intensity[9] -[12]), there are N_collapse ground motions induce the collapse of the structure. Then the collapse possibility will be N_collapse / N_total. By increasing the intensity of ground motion, the relationship between intensity and the collapse possibility can be obtained, which is the collapse fragility curve of the structure. The collapse fragility curve could give a quantitative evaluation of seismic collapse resistance.

2.2 Collapse margin ratio

A collapse resistance index that is referred as collapse margin ratio (CMR) [8] is proposed by Applied Technology Council of USA, which is defined by

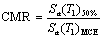                                                                          (1)

where S_a(T₁)_50% is the intensity that causes 50% of collapse according to the collapse fragility curve, and S_a(T₁)_MCE is the intensity of maximal considered earthquake (MCE), which can be found from Table 5.1.4-1 in the Chinese Seismic Design Code.

CMR is an index for the evaluation of seismic collapse resistance based on probability theory which has already considered the influence of earthquake uncertainty. Therefore, although CMR analysis still has some problems (e.g. whether the representative of ground motion records is sufficient, whether the numerical model of collapse is reasonable), it provides a relatively reliable standard to the collapse resistance evaluation of different structures.

2.3 THUFIBER program and collapse criterion

The collapse of structures is a complex nonlinear dynamic process. Traditionally, because of the limitation of computational capacity, indirect methods, such as the ultimate inter-story drift, are generally adopted as collapse criterion, which is not rational. For example, the ultimate inter-story drift in the Code of different countries (e.g. China and America) may have a quite big difference. As the computation method developed, nonlinear analysis program now can simulate the entire nonlinear process of structural collapse accurately, with material nonlinearity, geometric nonlinearity and contact nonlinearity considered. This paper adopts THUFIBER program, developed by Tsinghua University based on MSC. MARC, to simulate collapse of structures [13][14][15]. THUFIBER program can stably simulate the entire process of collapse of complex RC structure during earthquake, whose details are shown in Ref [13][14][15] . Therefore, this paper takes the real physical definition of collapse, which is: ¡°Structure loses so much vertical strength that it cannot preserve sufficient space for people to live in safely¡± as the collapse criterion.

3.    Structural models and parameters

24 RC frames, of which each has the equal spans and storey heights, in 7-degree seismic fortification zone are designed according to the Chinese Seismic Design Code GB50011-2001 with PKPM software. The concrete strengths of beams are C30 while the concrete strengths of columns are listed in Table 1. The longitudinal reinforcements of beams and columns are HRB335 rebar (f_y=335MPa) while the stirrups are HPB235 rebar (f_y=235MPa). The dead loads (DL) on the floor and roof are both 7kN/m² (including the dead weight of the slab) while the live loads (LL) are both 2kN/m². The major parameters of the 24 frames are shown in Table 1. Influences of span, storey height and storey number to seismic collapse resistance of RC frames are mainly considered. Because the frames have regular plane layouts, a typical planar frame is selected to buildup the nonlinear model for analysis. The structural gravity loads are concentrated to the beams and columns with the load combination of 1.0DL+0.5LL.

Table 1. Parameters of structural models

4.    Calculation results and discussions

4.1 Typical modes of collapse

The typical collapse modes of frames are shown in Fig. 1 (plastic-hinge regions are plotted by grey contour and marked with ¡ð). When frames collapse, plastic hinges have already appeared on every beam, which reflects that the principle of ¡®strong column and weak beam¡¯ could basically be achieved in these frames if the enhancement of floor slab and over-reinforcement of beam are not considered.

With seismic intensity increasing, more plastic hinges appear on columns gradually. Collapses all start from the compressive failure at the feet of middle columns of bottom story (indicated by ellipses in Fig. 1) which are under small eccentric compression. By comparing Fig. 1(a)(b)(c), it could be found that the quantity of plastic hinges on columns becomes less when the span increases. The frame with 8m span only has plastic hinges at the feet of bottom columns and there are almost no column hinges in above stories, which results in much smaller energy dissipation capacity compared with the frames with 4m or 6m span. Therefore, the frame with 8m span has the worst seismic collapse resistance.

4.2 Collapse fragility curves

The collapse fragility curves of different frames are shown in Fig. 2~4. According to ATC-63 Report [8] , in order to achieve the objective that the collapse possibility of structure under maximal considered earthquake is less than 10%, the acceptable value of CMR should be larger than 2.30 (based on the numerical models in this work), shown as the vertical dash lines in Fig. 2~4.

4.2.1 Comparison for different spans

All 24 frames are divided into 8 groups to compare the influence of span to the fragility curves, as shown in Fig. 2. It can be found that the collapse possibility becomes larger as span increases. The reason is that the increase of span leads to the increase of total gravity loads, which results in larger axial compression ratios of columns (shown in Table 1). For these columns under small eccentric compression, the bending strength and ductility decrease with larger axial compression ratio, which makes the column feet crush before the ductility of whole structure could be fully developed. In Wenchuan Earthquake, many classroom buildings with large span collapsed while office buildings and residences with small span shown less damage. It may be due to this reason [1][3][4].

4.2.2 Comparison for different storey numbers

The frames are divided into 6 groups to compare the influence of story number, as shown in Fig. 3. Generally higher frames with larger axial compression ratios are more vulnerable to collapse.

4.2.3 Comparison for different storey heights

The frames are divided into 4 groups to compare the influence of story height, as shown in Fig. 4. Most frames with 3.6m storey height have better collapse resistances than those with 2.8m storey height, especially for frames with smaller span or storey number. It is because storey height has two aspects of effect on the seismic collapse resistance of frames:

(1) Positive effect: Structures with different storey height has almost the same axial compression ratio of column, which results in close rotation capacity of plastic hinges at the ends of columns. Therefore, as storey height increases, ultimate deformation of column increases so that the energy dissipation capacity of structure increases. Then the seismic collapse resistance of whole structure increases.

(2) Negative effect: As storey height increases, the lateral displacement of structure will result in larger of P-D effect of the whole structural system and P-d effect of single column. Then the seismic collapse resistance of structure will be weakened.

For frames with small span and storey number, the positive effect is more obvious, while for frames with large span and storey number, the negative effect reduce the positive effect, which makes the influence of storey height less obvious.

Figure 4. Comparison for collapse fragility curves of frames with different storey heights

4.3 Collapse possibility under severe earthquake and mega-earthquake

Collapse possibilities of frames under severe earthquake (maximal considered earthquake in the Chinese design code) and mega-earthquake are shown in Table 2. ATC-63 Report [8] proposes 10% of collapse possibility as the acceptable criterion for the structural collapse resistance under MCE. It can be found that for frames with 4m span, the collapse possibilities under MCE are all smaller than 10%. But the collapse possibilities under MCE of most frames with 6m or 8m span are larger than 10%. And the results of frames with 8m span are especially worse.

Table 2. Collapse possibilities of frames under severe earthquake and mega-earthquake

Because of the economic limitation in China and similar developing countries, the structures may experience earthquakes that are much larger than the maximal considered earthquake in currently Chinese design code. For example, the seismic fortification intensity of most heavy damaged areas in Wenchuan Earthquake is 7 degree, which means the intensity of designed maximal considered earthquake is 8 degree, but the actual intensity of some areas reached 9¡«11 degree. Therefore, it is necessary to analyze the seismic collapse resistance of structures under earthquake that is larger than the maximal considered earthquake. In this work, earthquakes whose intensity is twice of the MCE (S_a(T₁) =2.0S_a(T₁)_MCE) is considered as the mega-earthquake. And from the collapse fragilities curves, the collapse possibilities of frames under mega-earthquake are shown in Table 2. Collapse possibilities of most frames with 4m span under mega-earthquake are less than 20%, while collapse possibilities of most frames with 6m or 8m span are over 50%, especially for those with 8m span. Therefore, it is necessary to do some further research on improving seismic collapse resistance of Chinese structures under mega-earthquake.

4.4 Collapse margin ratio

CMR of each structure could be obtained from Eq (1) and the collapse fragility curves in Fig. 2~4. The CMR of different frames are shown in Table 3. According to ATC-63 Report, considering the influence of uncertainty, the limitation of CMR should be 2.30 to ensure that the collapse possibility of structure under MCE is less than 10%. It can be found that CMR of most frames with 4m span are larger than 2.3, which means their seismic collapse resistances could meet the request. But CMR of most frames with 6m or 8m span are smaller than 2.30, which mean their seismic collapse resistances are not enough.

Table 3. Collapse margin ratios of frames

5.    Conclusions

This paper analyzes seismic collapse resistances of 24 RC frames in 7-degree seismic fortification zone, which have different spans, storey heights and storey numbers, designed according to the Chinese Seismic Design Code. The result shows that although all designed according to the Code, frames with different structural parameters have great differences on their seismic collapse resistances under severe earthquake and mega-earthquake. The reason is that the frames with large span or storey number have larger axial compression ratios of columns, which results in smaller bending strength and ductility of columns, as well as the energy dissipation capacity of the whole structure. So controlling the axial compression ratio will be critical to improve the collapse resistance of Chinese frames.

Acknowledgement

The authors are grateful for the financial support received from National Science Foundation of China (No: 90815025) and National Scientific and Technical Supporting Programs of China (No: 2009BAJ28B01).

References:

[1]         Analysis on Building Seismic Damage in Wenchuan Earthquake, Journal of Building Structures, 2008, 29(4): 1-9.

[2]         GB50011-2001, Code for seismic design of buildings [S], Beijing: China Architecture and Building Press, 2001.

[3]         Ye LP, Qu Z, Lu XZ, Feng P, Collapse prevention of building structures: a lesson from the Wenchuan earthquake, Journal of Building Structures, 2008, 29(4): 42-50.

[4]         Ye LP, Lu XZ, Zhao SC, Li Y, Seismic collapse resistance of frame structures----Case studies on the seismic damages of several frame structures under extreme ground motion in Wenchuan Earthquake, Journal of Building Structures, Accepted.

[5]         Applied Technology Council, Seismic evaluation and retrofit of concrete buildings[S]. ATC-40, 1996.

[6]         FEMA273, FEMA274, FEMA356, NEHRP Guidelines for the Seismic Rehabilitation of Buildings[S]. Washington D C: Federal Emergency Management Agency, 1996.

[7]         Bertero V V. Strength and deformation capacities of buildings under extreme environments. Structural Engineering and Structural Mechanics,1977, 29-79.

[8]         Quantification of building seismic performance factors, ATC-63 Project Report (90% Draft), FEMA P695 / April 2008

[9]         Bazzurro P, Cornell C A, Shome N, et al. Three proposals for characterizing MDOF non-linear seismic response. Journal of Structural Engineering, 1998, 124(11): 1281-1289.

[10]     Vamvatsikos D, Cornell C A. Incremental dynamic analysis. Earthquake Engineering and Structure Dynamics, 2002, 31(3): 491-514.

[11]     Shome N, Cornell CA. Probabilistic seismic demand analysis of nonlinear structures. Report No. RMS-35, Reliability of Marine Structures Program, Department of Civil Engineering, Stanford University, Stanford, CA, 1999.

[12]     Ye LP, Ma QL, Miao ZW. Study on earthquake intensities for seismic analysis of structures. Earthquake Engineering and Engineering Vibration, 2009, 29(4): 150-163.

[13]     Wang XL, Lu XZ, Ye LP, Numerical simulation for the hysteresis behavior of RC columns under cyclic loads [J], Engineering Mechanics, 2007, 24(12): 76-81.

[14]     Ye LP, Lu XZ, Ma QL, Wang XL, Miao ZW, Seismic nonlinear analytical models, methods and examples for concrete structures [J], Engineering Mechanics, 2006, 23(sup. II). 131-140.

[15]     Lu XZ, Lin XC, Ma YH, Li Y, Ye LP, Numerical simulation for the progressive collapse of concrete building due to earthquake, Proc. the 14th World Conference on Earthquake Engineering, October 12-17, 2008, Beijing, China, CDROM.