2. EXISTING INTENSITY MEASURES
Published literature (Tothong and Luco 2007; Cordova et al. 2001; Luco and Cornell 2007; Baker and Cornell 2005; Vamvatsikos and Cornell 2005; Ye et al. 2013) indicates that the existing IMs can be classified into two types: scalar- and vector-valued. Scalar IMs can be further categorized into single-parameter and multi-parameter IMs according to the number of parameters required.
The traditional peak values of ground motion records such as PGA, PGV and PGD are typical single-parameter scalar IMs. These IMs are still widely used in many national design codes because of their simplicity (MOC 2010; The Building Centre of Japan, 2000). Some recent literature indicates that PGA or PGV IMs, which only consider the characteristics of ground motions, do not perform well in predicting structural responses within short to medium periods. Therefore, the 5%-damped elastic spectral acceleration Sa(T1) at fundamental period T1 (Shome et al. 1998) has been widely used for these periods. Sa(T1) covers not only the characteristics of ground motions but also the dynamic features of the structures. Compared with PGA, the dispersion of the predicted structural responses based on Sa(T1) is remarkably reduced (Ye et al. 2013), particularly for first-mode-dominated, moderate period structures. Despite these advancements, Sa(T1) only deals with the characteristics of the elastic fundamental period of the structure. When progressing into the nonlinear stage, the fundamental period of a structure elongates gradually, leading to changes in the structural dynamic characteristics. Furthermore, for high-rise buildings, higher-order vibration modes greatly influence the structural responses. All these factors however were not considered in the Sa(T1) formulation (Lucchini et al. 2011).
To overcome the aforementioned limitations, various attempts have been made to improve Sa(T1) by considering the effect of period elongation and the contribution of the higher modes (Tothong and Luco 2007; Cordova et al. 2001; Vamvatsikos and Cornell 2005). For example, Cordova et al. (2001) proposed an IM called S * a, which is based on the fundamental period T1 and the longer period Tf representing the inelastic (damaged) structure S * a, also taking into consideration the period elongation in the nonlinear stage, as expressed by Eqn 1 below:
![]() ,
(1)
,
(1)
where a and c are two parameters to be calibrated.
Note that the dynamic behavior of buildings upon entering into the nonlinear stage is not fully understood, particularly at the early stage of structural design because of the difficulties in accurately predicting the nonlinear behavior of the building. Consequently, IMs that consider period elongation are limited in scope and practical application.
With respect to the higher vibration modes,
the IM proposed by Vamvatsikos and Cornell (2005) also considers the
participation of higher-order vibration modes. In the expression ![]() , the values of ta
and tb
represent the higher modal periods of concern.
, the values of ta
and tb
represent the higher modal periods of concern.
Similarly, Luco and Cornell (2007) proposed an IM called IM1E&2E based on the first two vibration modes and the square-root-of-sum-of-squares (SRSS) rule of modal combination. This IM considers the effect of the contribution of higher modes caused by the near-fault pulse, as expressed in Eqn 2.
where ![]() and Sd(T1,z1)
and Sd(T2,z2)
are the elastic spectral displacements, respectively,
at damping ratios z1 and z2 with corresponding periods T1
and T2. Eqn 2 also defines the jth ¨C mode
participation factor for the story drift ratio of the ith
story, qi,
as
and Sd(T1,z1)
and Sd(T2,z2)
are the elastic spectral displacements, respectively,
at damping ratios z1 and z2 with corresponding periods T1
and T2. Eqn 2 also defines the jth ¨C mode
participation factor for the story drift ratio of the ith
story, qi,
as ![]() . Note that PF[2] 1 denotes the first mode
participation factor for the maximum peak inter-story drift angle,
qmax, obtained using the
SRSS of the first two modes. Similarly, PF[1] 1 represents the
first-mode participation factor for qmax
when only the first mode is considered. The coefficient
. Note that PF[2] 1 denotes the first mode
participation factor for the maximum peak inter-story drift angle,
qmax, obtained using the
SRSS of the first two modes. Similarly, PF[1] 1 represents the
first-mode participation factor for qmax
when only the first mode is considered. The coefficient ![]() reflects the effect of the second mode on
qmax
and the relevant spectral shape. The coefficient
reflects the effect of the second mode on
qmax
and the relevant spectral shape. The coefficient ![]() mainly indicates the influence of the first-mode
and first-two-modes estimations on qmax, which may occur on different stories. The
earlier proposed IM1E&2E has also been
improved by the same researchers (Luco and Cornell 2007), where the inelastic
spectral displacement SI d(T1,z1,dy) was adopted as a replacement
for the elastic spectral displacement Sd(T1,z1). The new IM is called IM1I&2E.
Despite the advancement of IM1E&2E and
IM1I&2E, their complex expressions render
the various parameters difficult to be determined, especially at the early
design stage, thus limiting practical application of these IMs.
mainly indicates the influence of the first-mode
and first-two-modes estimations on qmax, which may occur on different stories. The
earlier proposed IM1E&2E has also been
improved by the same researchers (Luco and Cornell 2007), where the inelastic
spectral displacement SI d(T1,z1,dy) was adopted as a replacement
for the elastic spectral displacement Sd(T1,z1). The new IM is called IM1I&2E.
Despite the advancement of IM1E&2E and
IM1I&2E, their complex expressions render
the various parameters difficult to be determined, especially at the early
design stage, thus limiting practical application of these IMs.
In addition to the aforementioned scalar IMs, some vector-valued IMs have also been proposed in recent years. For example, Baker and Cornell (2005) proposed a two-parameter vector-valued IM called <Sa(T1), e>. The definition of parameter e is originated from seismology engineering. This parameter reflects not only the distinction of the spectral shapes but also, to some extent, the effect of higher-mode contribution and period elongation. However, due to the absence of the basic data required to obtain e in many countries, more work must be performed before the vector-valued IM <Sa(T1), e> can be applied worldwide.
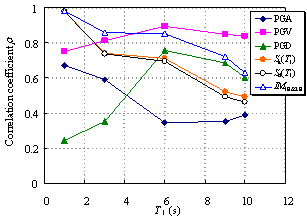
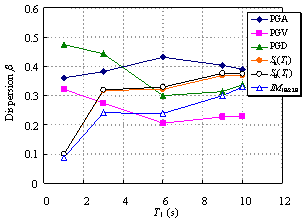
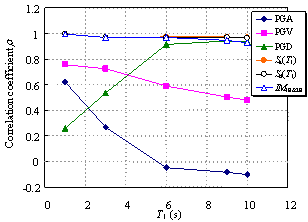
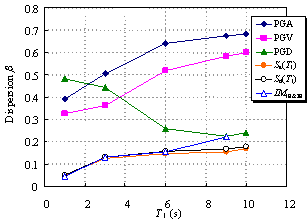
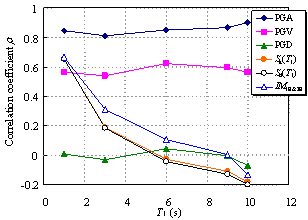
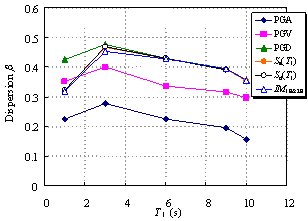
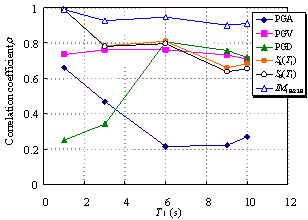
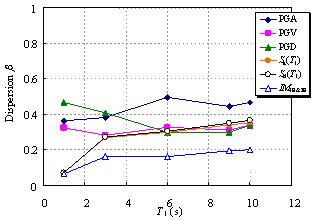
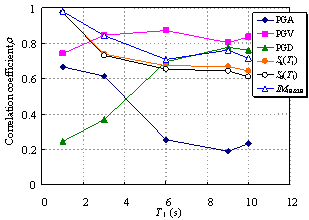
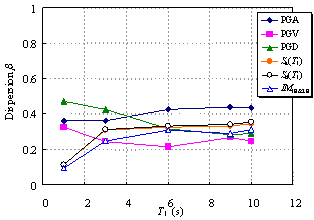
Ye et al. (2013) compared the applicability of 18 commonly used IMs in an elasto-plastic analysis of different buildings. The findings indicated that Sa(T1) has the best correlation with the structural demand measures (DMs) for short- and moderate-period structures. In addition, the correlation between PGV and the DMs is also acceptable. Furthermore, PGV performs better as an IM when the fundamental period of the structure increases. Based on their study, Sa(T1) and PGV have been recommended for use as the IMs in actual structural design.
Existing research on IMs as outlined above has mainly targeted structures whose fundamental periods are shorter than 6 s and mostly in the range of 0 to 4 s. It is evident that the rationality of the existing IMs requires further validation for super high-rise buildings with fundamental periods as long as approximately 10 s. This validation is the focus of the present study, with an emphasis on the actual requirements of structural design. A total of six different IMs (PGA, PGV, PGD, Sa(T1), Sd(T1), and IM1E&2E) are evaluated and their rationalities are discussed. PGV and Sa(T1) were selected based on the recommendations of Ye et al. (2013). To consider the contribution of the higher-order vibration modes of super high-rise buildings, IM1E&2E was also selected. In addition, PGA, PGD and Sd(T1) were considered because they are widely used in actual design. The correlation between the IMs and DMs with different vibration periods is analyzed, and rational IMs for super high-rise building design are recommended.
3. ANALYTICAL MODEL AND GROUND MOTION SELECTION
3.1 Simplified analytical model
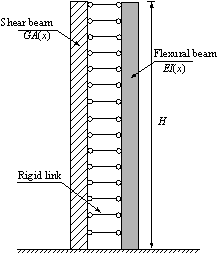
This study mainly focuses on super high-rise buildings with very long fundamental vibration periods. In general, the commonly used lateral seismic-resistant super high-rise systems include framed tube, bundled tube, tube-in-tube, diagonalized (trussed tubes, diagrids or braced frames), core and outrigger (central lateral system linking to the perimeter system through outriggers) and hybrid systems (Lu et al. 2011). The deformation modes of these structural systems are typically a combination of flexure and shear, which differs greatly from the traditional frame or shear wall buildings. This implies that the traditional multistoried shear model and cantilever flexural beam model are not suitable for super high-rise buildings. Consequently, the dynamic properties and seismic responses of super high-rise buildings are approximated herein by using an equivalent continuum model consisting of a shear and a flexural cantilever beam, which is proposed by Miranda and Taghavi (2005) (Figure 1). The shear and flexural cantilever beams are connected by an infinite number of rigid links to achieve horizontal deformation compatibility at the same height. The response of this model subjected to ground acceleration can be expressed in the following partial differential equation:
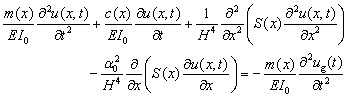 ,
(5)
,
(5)
where u(x,t) is the horizontal displacement at non-dimensional height x at time t; m(x) is the mass per unit length of the model; x varies between 0 at the base of the building and 1 at the roof level; ug(t) represents ground displacement at time t; H denotes the total height of the model; and EI(x) and GA(x) are, respectively, the flexural stiffness of the flexural beam and the shear stiffness of the shear beam at non-dimensional height x. Miranda and Taghavi (2005) assumed that the variations in the shear and flexural stiffness along the height are identical, i.e., S(x) or
|
EI(x)=EI0S(x) |
(6) |
|
(7) |
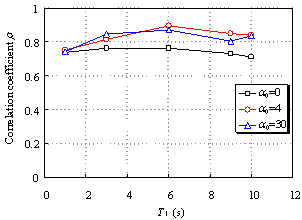
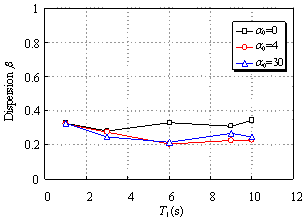
in which, S(x) is the dimensionless function that defines the variation of stiffness along the height of the simplified model, and EI0 and GA0 are, respectively, the flexural and shear stiffness at the base of the model. The dimensionless parameter a0=H(GA0/EI0)1/2 controls the proportions of the flexural and shear deformations in the simplified model and thus the lateral deformation shape of the building. Theoretically, when a0=0, the model degenerates into a pure bending model, and when a0=¡Þ, it degenerates into a pure shear model. Miranda and Taghavi (2005) indicated that a0 is normally between 0 and 1.5 for shear wall buildings; between 1.5 to 5 for buildings with dual structural systems consisting of a combination of moment-resisting frames and shear walls; and between 5 and 20 for moment-resisting frame buildings. In addition, when a0¡30, the deformation mode is dominated by shear deformations. A number of different buildings were analyzed by Miranda and Taghavi (2005) to verify the appropriateness of the model in simulating the elastic vibration of different buildings.
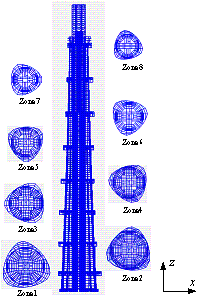
To ensure the appropriateness of the simplified model, the 632 m super high-rise building Shanghai Tower (see Figure 2) is selected herein to calibrate the key parameters used in the model. The Shanghai Tower has a hybrid lateral seismic-resistant system called the ¡°mega-column/core-tube/outrigger-truss¡±. According to architecture and functional requirements, eight reinforced stories were built for every 13 to 16 stories, which divide the entire structure into eight zones. The plane layouts of these eight stories are also briefly illustrated in Figure 2. The fundamental period of the Shanghai Tower is nearly 9.83 s (Lu et al. 2011), which is far beyond the range of 6 s specified in the design response spectrum of the Chinese Code for the Seismic Design of Buildings (MOC 2010).
The parameters of the simplified model are calibrated such that the fundamental dynamic properties of the simplified model approach those of the Shanghai Tower in the XZ plane. The total gravitational load of the simplified model, which is determined from a combination of 1.0 D + 0.5 L, is identical to that of the Shanghai Tower, in which D is the dead loads, including the effects of self weight and permanently attached equipment and fixtures; L is the live loads. Note that the dead and live loads of the Shanghai Tower have little variation along its height; the simplified model thus has a constant mass distribution along the height. According to the stiffness distribution of the Shanghai Tower, a quadratic curve, i.e., S(x)=1-(1-0.55)x2, is adopted to model the structural stiffness along the height (Eqns 6 and 7). The flexural stiffness at the base, EI0, and the dimensionless flexural and shear ratio, a0, are calibrated according to the dynamic properties of the Shanghai Tower.
The values of the main parameters used in the simplified model are summarized in Table 1. The first five free translational vibration periods and the relative deviation D between the simplified model and the fine FE model of Shanghai Tower are compared in Table 2. The relative deviation D, defined by Eqn 8, is adopted to describe the distinction between the two models. In the equation, Tsimplify and Tfine represent, respectively, the free translational vibration periods of the simplified model and the fine FE model of Shanghai Tower.
|
D = (Tsimplify - Tfine) / Tfine |
(8) |
It is evident that some discrepancies are present in the comparison. Note that a substantial reduction in computational costs is achieved by employing the simplified model compared with a very fine FE model. Note also that the focus of this study is to offer a general rule for super high-rise buildings instead of investigating the characteristics of a particular structure. Therefore, the resulting discrepancies are considered acceptable.
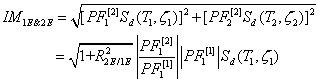
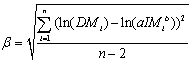 (11)
(11)