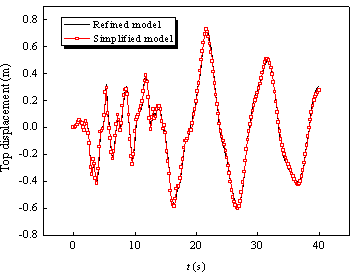
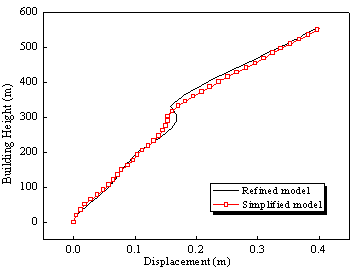
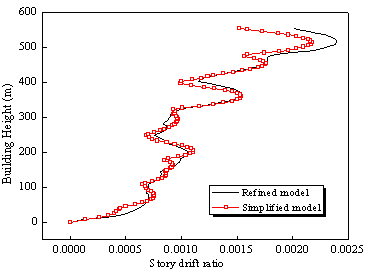
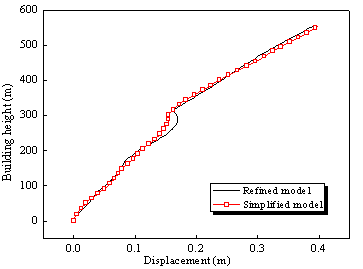
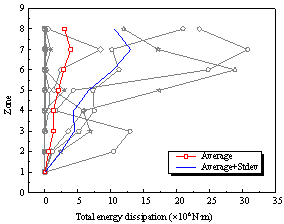
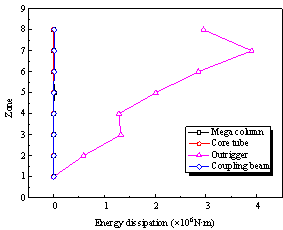
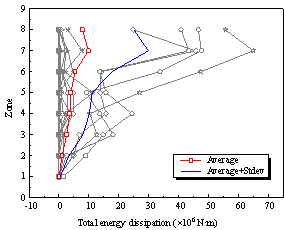
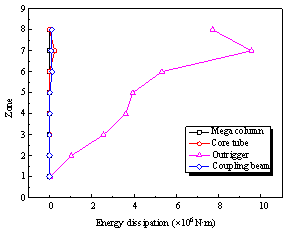
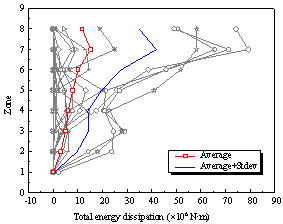
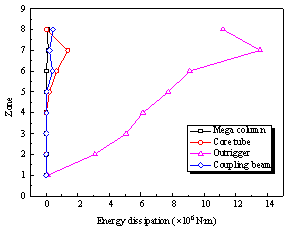
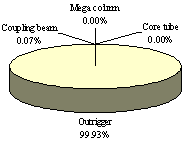
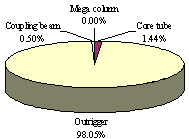
|
3.
ESTABLISHMENT OF THE SIMPLIFIED MODEL
3.1
General provisions of the simplified model
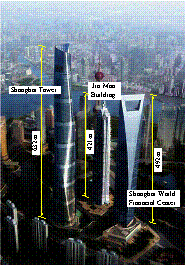
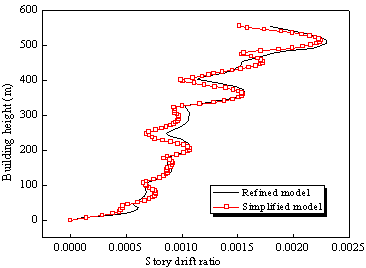
To develop a simplified model of the Shanghai
Tower, the following assumptions are made. The major objective was to characterize
the plastic energy dissipation and dynamic properties of the structural components
and system during seismic analysis.
(1) The
three-dimensional (3D) refined FE model is used to develop the planar simplified
model. The fundamental periods in the x and y directions of
the 3D refined FE model are approximately 9.27 s and 9.19 s, respectively,
indicating that the lateral stiffness in the two orthogonal directions is
very similar. The first torsion period is approximately 4.09 s, and the torsion-translational
period ratio is approximately 0.416 that is much smaller than 0.85 limit specified
in the Technical Specification for Concrete Structures for Tall Buildings
(JGJ 3-2010) [20]
. It can be concluded that the significance of torsional effects in
the Shanghai Tower is not predominant,
and it is therefore feasible to simplify it into a planar model to primarily
focus on the translational dynamic effects in seismic analysis.
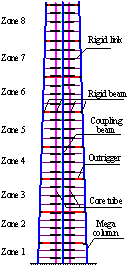
(2) The
mega columns, core tube (including the shear walls and coupling beams) and
the outrigger receive primary consideration in the simplified model and other
components, such as secondary steel frames, are not included in the model.
The selection of these components is based on the contribution of these components
to the total lateral stiffness of the refined 3D FE model of the Shanghai
Tower. The details of this procedure can be described as
follows: To determine the stiffness contribution of various components
in the refined FE model, the stiffness of each type of component (including
the secondary frame, the mega column, the core tube and the outrigger) is
reduced by 50%, while the total mass and all properties of other components
remained unchanged. The first nine vibration periods of the reduced stiffness
model and the original model are compared in Table 1. When the stiffness of
the secondary steel frame is reduced the change in period is very small¡ªall
are less than or equal to 0.35%. It can be concluded that the contribution
of the secondary steel frame to the total structural lateral stiffness is
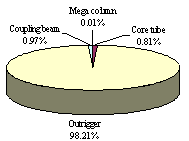
negligible and can be ignored in the simplified model. When the stiffness
of the mega columns is reduced by 50%, the change in translational periods
is significantly large. The change in the fundamental period is approximately
15%, and it gradually decreases for higher vibration modes. However, the influence
on the torsional periods is relatively small at approximately 2.58%. This
suggests that the mega columns significantly contribute to the lateral stiffness
of the entire building and this contribution is more obvious in the fundamental
translational periods than in the higher mode periods. A 50% reduction in
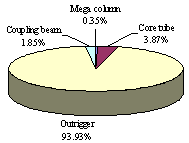
the stiffness of the core tube results in a large increase in all modal periods
with more increase in the periods of higher vibration modes. The reduction
in core tube stiffness also has a great impact on the torsional mode periods
- an approximately 28% increase in torsional periods. These results indicate
that the core tube stiffness has great contributions to both the structural
lateral and torsional stiffness of the entire building. In addition, because
the flexural deformation is predominant in the high order vibration modes
and the core tube stiffness has significant impact on the flexural stiffness,
the core tube stiffness contributes more to the stiffness of the higher order
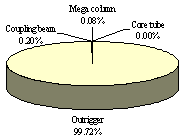
vibration modes. Finally, a reduction in the stiffness of the outrigger leads
to a conclusion similar that of the mega columns. That is, the outrigger significantly
contributes to the lateral stiffness of the building and has a smaller contribution
to its torsional stiffness. Based on the above conclusions, the mega column,
the core tube (including the shear wall and the coupling beam) and the outrigger
are the primary components that need to be properly modeled in the simplified
model of the Shanghai Tower.
(3) Nonlinear beam-column elements and nonlinear spring elements
are adopted to model components in the simplified model. To make the simplified
model easy to implement, the mega column, shear walls and the outrigger are
simulated by nonlinear beam-column elements. Many research studies have been
conducted to simulate columns and shear walls using nonlinear beam-column
elements and springs under seismic loads. For example, Ibarra et al. [21] proposed a
hysteretic model that incorporates strength and stiffness
deterioration to simulate beams and columns. Subsequently, this model has
been adopted to simulate the global collapse of frame structures subjected
to earthquakes [22]
, and it has been widely used. Rodrigues et al. [23]
proposed a simplified hysteretic model to simulate the biaxial bending
response of reinforced concrete columns. Setzler & Sezen [24]
and Sezen & Chowdhury [25]
simulated columns using flexural elements and nonlinear springs under
lateral loads including the effect of strength and stiffness degradation that
may be caused by shear or axial failure. Similarly, Orakcal & Wallace
[26] used
a beam-column element to simulate the flexural behavior of a reinforced concrete wall, and they
also verified the rationality of this model with experimental data.
Table
1 Reduction in period of the original 3D model (%) when the component stiffness
is reduced by 50%
| |
|
Change in period
|
| |
|
secondary frame
|
mega columns
|
core tube
|
outriggers
|
|
T1
|
1st Translational mode in x-direction
|
0.27%
|
15.3%
|
11.17%
|
9.12%
|
|
T2
|
1st Translational mode in y-direction
|
0.26%
|
15.1%
|
11.46%
|
8.94%
|
|
T3
|
1st Torsion mode
|
0.26%
|
2.58%
|
27.76%
|
2.64%
|
|
T4
|
2nd Translational mode in x-direction
|
0.35%
|
5.24%
|
21.91%
|
6.36%
|
|
T5
|
2nd Translational mode in y-direction
|
0.34%
|
5.34%
|
22.12%
|
6.22%
|
|
T6
|
2nd Torsion mode
|
0.30%
|
2.31%
|
28.36%
|
3.01%
|
|
T7
|
3rd Translational mode in x-direction
|
0.31%
|
2.90
|
27.38%
|
4.28%
|
|
T8
|
3rd Translational mode in y-direction
|
0.31%
|
3.00%
|
27.28%
|
4.33%
|
|
T9
|
3rd Torsion mode
|
0.33%
|
2.01%
|
29.34%
|
2.7%
|
Because
the planar simplified model is developed in this paper, the nonlinear beam-column
element has three independent DOF (i.e., two translational DOF and one rotational
DOF) with each DOF assigned to the corresponding cross-section-based hysteretic
model. The hysteretic model proposed by Lu et al. [27]
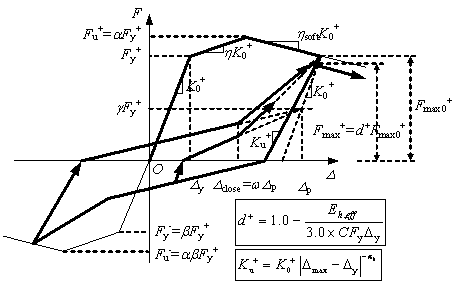
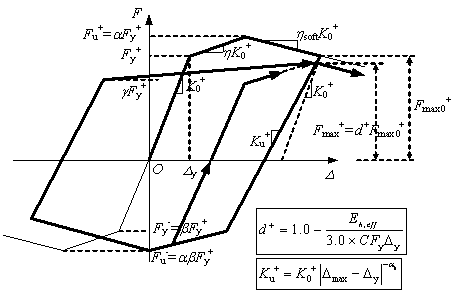
is adopted in this paper. The model is illustrated in Figure 3. The
model considers not only the yielding, hardening and softening behavior but
also the pinching and strength and stiffness deterioration effects under cyclic
loading. Additionally, this model also demonstrates the phenomena of reversed
yielding strength not equal to the positive yielding strength. The parameters
in this model can be divided into two groups. The first group of parameters
define the backbone curve, including K0
(the initial stiffness), Fy (the generalized yielding strength,
e.g., axial force, shear force, or bending moment), h (the hardening ratio), hsoft (the softening
ratio), a (the
ratio of peak strength and yield strength) and b (the ratio of reversed yield strength
and positive yield strength). The
second group of parameters controls the hysteretic behavior, including g
(representing the pinching effect), w
(representing the position of the ending point of slip), C (dimensionless
accumulated hysteretic energy dissipation parameter, which reflects the capacity
of resisting strength degradation caused by the cyclic loading.) and ak
(defining unloading stiffness). The values of these hysteretic parameters
in the simplified model are obtained from numerical simulations and hysteretic
component tests. Using a wide range of experimental data, Lu et al.
[27] and
Qu & Ye [28]
showed that the hysteretic model can successfully simulate the nonlinear
behavior of a variety of different components. Similarly, many simplified
models have been proposed to simulate the cyclic response of coupling beams.
For example, a beam element with two moment-hinges at the two ends and a shear-hinge
in the middle was adopted to simulate the coupling beam in ATC 72 [29] . Therefore,
in this paper, this model is used to simulate the coupling beam in the simplified
model.
(4) The
values of the hysteretic parameters for different components in the simplified
model are determined using the refined FE model simulation results and the
conventional component hysteretic tests. Because the dimensions of the components
in the Shanghai Tower are very large, it is difficult to find similar component
tests to calibrate the values of the hysteretic parameters. Therefore, the
values of the hysteretic parameters in Figure 3 are determined according to
the following two principles: (a) using the refined FE model with component
dimensions, the force-displacement backbone curve under the cyclic lateral
loads can be simulated, and then the backbone curve parameters (K0,
Fy, h,
hsoft,
a
and b) can be obtained; (b) By taking into account
the difficulties in simulating the hysteretic properties of the concrete components
with the refined FE model, the values of the hysteretic parameters in Figure
3 (g, w,
C and ak)
can be obtained from the conventional component hysteretic
tests, if such experiments are reported in the literature. Due to the
size effect of the conventional components in the tests, these parameters
may not be very accurate, so a special parametric study is conducted later
in this paper to show that the values of these hysteretic parameters do not
have a significant impact on the overall simulation results.
The final
simplified model of the Shanghai Tower is established according to the above
assumptions, and the model is shown in Figure 2b. Note that the 3D refined
FE model has approximately 120,000 elements and 441,000 DOF, and the model
size significantly decreases to approximately 2,500 elements and 7,200 DOF
in the simplified model.
3.2
Simplified model for the mega column
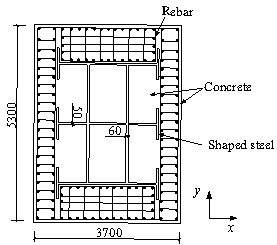
There are eight mega columns extending from the bottom
to the top of the Shanghai Tower and the maximum cross section of the mega
column is shown in Figure 4a. The mega column is constructed with concrete
reinforced by rebar and shaped steel. The area of this mega column section
is nearly 20 m2 and has a steel ratio of 6.22% and a reinforcement
ratio of 1.16%. The floor plan layout of these mega columns is shown in Figure
4b. Because these columns have similar strength and stiffness, the two mega
columns on each side of the building are simplified and modeled as a single
column as shown in Figure 4c. Results from the refined FE model showed that
the main stress state of mega columns is bending and compression. Therefore,
the nonlinear bending and compression behavior of the mega column is considered
in the simplified model, while the shear behavior is simulated as elastic.
The results from the refined FE model indicate that because the gravity load
of the building is very large, the corresponding static axial forces on the
mega columns are quite large. Therefore the axial force does not significantly
change when subjected to the MCE. Therefore, the coupling effect between the
axial force and the bending moment in mega columns can be disregarded.
Thus, the bending moment-curvature relationship under compressive axial loads
(due to gravity loading) is adopted to simulate the nonlinear flexural behavior
of the mega column.
The refined
FE models of mega columns from Zone 1 to Zone 8 (Figure 2a) are used to simulate
the flexural behavior under given constant axial loads, and the moment-curvature
backbone curves of these mega columns are obtained. One of the typical moment-curvature
backbone curves of the mega column is shown in Figure 5. Because
the steel-reinforced concrete mega columns in the Shanghai Tower have a maximum
cross sectional area of approximately 20 m2, it is difficult to
determine the hysteretic performance from a full-scale experiments. Consequently,
the hysteretic parameters of the mega columns in the simplified model are
calibrated using the hysteretic test data from conventional steel-reinforced
concrete columns, which have a similar steel ratio and axial load ratio to
the actual mega columns in the Shanghai Tower. Chen et al. [30] conducted a
hysteretic test of a steel-reinforced column with a 300 mm square cross section.
The longitudinal steel ratio and the design axial load ratio were approximately
7.22% and 0.65, respectively, which are comparable to those of the actual
mega columns in the Shanghai Tower. Therefore, the data from this hysteretic
test of the steel-reinforced concrete column is used to calibrate the hysteretic
parameters of the mega columns in the simplified model. The models shown in
Figure 3 are used to simulate the hysteretic performance of this steel-reinforced
column test. The results are compared in Figure 6, and the values of the hysteretic
parameters of the mega column in the simplified model are determined.
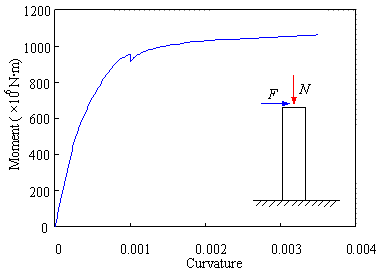
Figure 5 Typical bending moment-curvature
backbone curve under constant compression for a single mega column
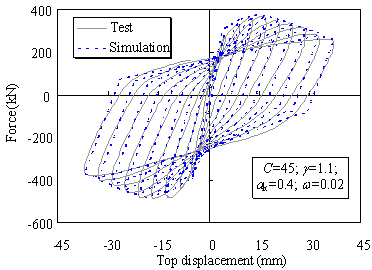
Figure
6 Comparison of the hysteretic test and simulation data for the steel reinforced
concrete column
3.3
Simplified model for the coupling beam
In Shanghai Tower, steel plate reinforced composite
coupling beams (i.e., a steel plate is embedded in the middle of the coupling
beams) are used instead of the traditional reinforced
concrete coupling beams to provide a higher stiffness and better ductility
than the traditional RC coupling beams. The typical layout of coupling beams
and walls in the core tube is shown in Figure 7. The distribution of the coupling
beam is regular and mainly distributed symmetrically along the two orthogonal
axes of the core tube. As the four coupling beams (referred to as A,
B, C, and D in Figure 7) divide the core tube into two
parts along the y axis, these four coupling beams are considered
in the simplified model as one equivalent coupling beam in each story.
Due to the constraint from the adjacent shear walls W1,
W2 and W3 (Figure 7), the two other coupling
beams (i.e., E and F in Figure 7) are simulated as a part of
the left or right half sub-tubes. Lu et al. [4]
indicate that the failure of the coupling beam is primarily due to
shear forces. Therefore, the coupling beam in the simplified model is simulated
by a shear spring element as shown in Figure 8. The refined FE model of typical
coupling beam in each story is developed, and the predicted backbone curve
of the shear force-displacement relationship of a typical coupling beam is
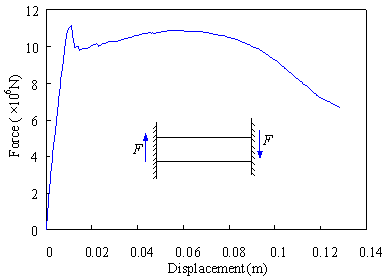
shown in Figure 9. This provides the backbone curve parameters of the hysteretic
model used in the simplified model. The other hysteretic parameters are calibrated
using steel plate reinforced composite coupling beam tests available in the
existing literature. Lam et al. [31]
conducted a series of hysteretic experiments on steel plate reinforced
coupling beams with different configurations. The cross-section of one typical
component was approximately 182 mm by 300 mm, and the thickness of the embedded
steel plate was approximately 10 mm. The span-height ratio was approximately
2.5. The shear spring model shown in Figure 8 is adopted to simulate the hysteretic
performance of the coupling beam, and the experimental and calculated responses
are compared in Figure 10. The hysteretic parameters of the coupling beam
can be determined from this comparison.
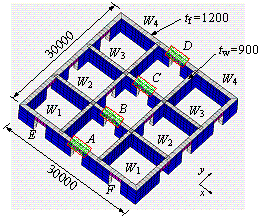
Figure 7 The distribution of the coupling
beams in typical core tube
(unit: mm)

Figure
8 The simplified model of the coupling beam
Figure
9 The backbone curve of the coupling beam
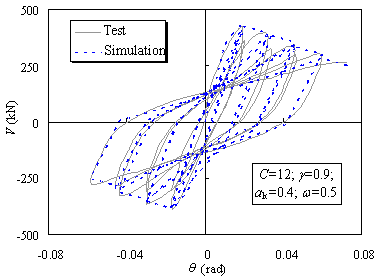
Figure
10 Comparison of the hysteretic test and the simulated response of the steel
plate reinforced coupling beam
3.4
Simplified model for the shear wall
The core tube is made up of a 30 m ¡Á 30 m RC tube; and
the thickness of the concrete flange (outer) walls decreases gradually from
1.2 m at the bottom to 0.5 m at the top. Similarly, the thicknesses of the
web (inner) walls decrease from 0.9 m at the bottom to 0.5 m at the top. The
typical planar section of the tube is shown in Figure 7. As mention above,
the layout of the coupling beams in the core tube is relatively regular and
the four coupling beams along the y-axis (Figure 7) divide the core
tube into two identical sub-tubes on the left and right side. These two sub-tubes
are simulated by two cantilever beams in the simplified model and connected
by coupling beams as described above. During the potential collapse process,
the failure of the core tube is dominated by axial compression and bending
[4] . In
addition, similar to the mega column, due to the large gravity loads, the
axial force variation in the core tube is insignificant under MCE loads. Thus,
the moment-curvature relationship under constant gravity/axial loads is adopted
to simulate the nonlinear flexural behavior of the core tube in the simplified
model.
The refined FE model of the sub-tube in each of the eight
zones is modeled one by one to simulate the flexural behavior under given
axial loads and then the moment-curvature backbone curves of these tubes are
obtained. A typical moment-curvature backbone curve is shown in Figure 11
and the corresponding backbone curve parameters are obtained. Hysteretic model
parameters (Figure 3) are obtained using experimental data from reinforced
concrete tube specimens tested under cyclic loads. Jia et al. [32]
tested a series of core tubes with 1380 mm¡Á1380 mm overall dimensions,
70 mm thickness, and a design axial load ratio of approximately 0.5, which
is comparable to that of the actual core tube in the Shanghai Tower. The beam-column
element and hysteretic model in Figure 3 are adopted to simulate the hysteretic
performance of the core tube specimen and to calibrate the hysteretic modeling
parameters. The comparison of the experimental and simulated response and
the obtained hysteretic parameters are shown in Figure 12.
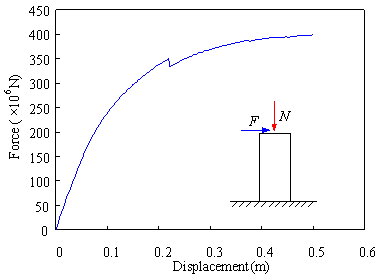
Figure 11 Lateral load-displacement backbone
curve for a typical core tube under axial compression
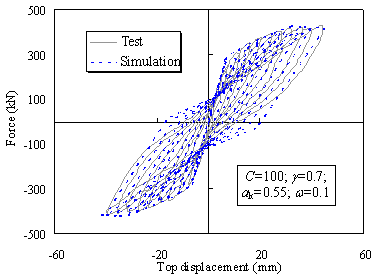
Figure
12 Comparison of the hysteretic test data and the simulated response of the
core tube specimen
3.5
Simplified model for the outrigger
The outriggers in the Shanghai Tower, with a height of
9.9 m, are located at the mechanical and refuge story levels. The horizontal
and diagonal members in the outrigger are made up of H-shaped steel. Main
dimensions of the typical outrigger are shown in Figure 13. The outrigger
is the major component connecting the inner core tube and the external mega
columns, thus making the building work as a unit. The outrigger is designed
mainly to resist the bending moment and the shear forces during an earthquake.
The bending moment is primarily resisted by the upper and lower horizontal
members (chords) while the shear force is generally withstood with diagonal
members (Figure 13). Because the coupling effect between the bending moment
and the shear force is not so obvious, a nonlinear flexural hinge and a shear
hinge are adopted, respectively, to simulate the bending and shear behavior
of the outrigger in the simplified model. First, a refined FE model of a typical
outrigger is analyzed to obtain the backbone curves under bending moment and
shear forces (Figure 14), and the backbone curve parameters are determined
from this simulation. Because there are few reported studies of hysteretic
tests of outriggers in the literature and the FE simulation of the steel components
is relatively reliable, the hysteretic performance of the outrigger is also
determined from the FE analysis. The cyclic shear responses obtained from
the simplified model and the refined FE model are compared in Figure 15, and
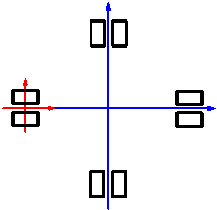
hysteretic modeling parameters are obtained. Each of the eight sets of outrigger
systems located at the two-story mechanical/refuge stories consists of 20
outriggers with an angle qi with respect to x-axis, as shown in Figure 16.
The strength and stiffness of each outrigger is projected to the x-axis
direction as a function of angle qi.
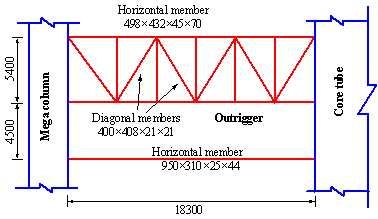
Figure 13 Details of a typical outrigger (unit: mm)
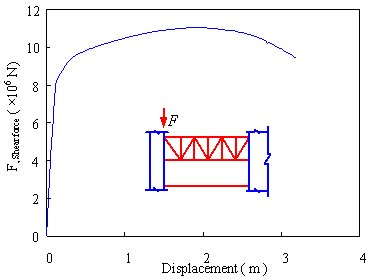
Figure 14 The backbone curve of the outrigger
subjected to shear
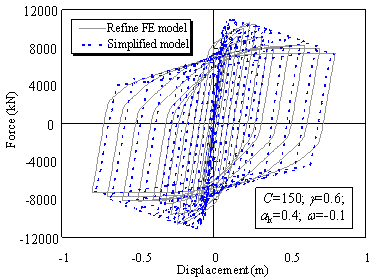
Figure 15 Cyclic shear response simulations
of the simplified model and refined FE model of the outrigger
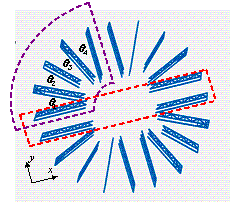
Figure
16 Spatial arrangements of the outriggers
3.6
Other modeling assumptions
The core tube and mega columns have a specified width
in the refined FE model. In contrast, the simplified beam-column element cannot
reflect this actual width in the simplified 2D model of the building. Therefore,
rigid arms with a certain length are inserted at the junction between the
mega columns and the core tube, as well as at the connections between the
coupling beam and the shear wall in each story. The lengths of the rigid arms
are determined from the actual width of the mega column or the core tube where
the rigid arms are connected. Rigid links are inserted between the mega column
and the core tube to represent the constraint of
the floor slabs. Because the raft foundation with piles is adopted for the
Shanghai Tower, which well constrains the displacement of the basement of
the Shanghai Tower, both the refined FE model and the simplified model are
fixed at the bottom. The soil-structure interaction effect and the energy
dissipated by the adjacent soil are neglected in this paper. The final simplified
model is shown in Figure 2b. Typical values of the hysteretic parameters for
different components in Zone 1 are summarized in Table 2.
Table 2 Typical values of the hysteretic parameters of
different components in Zone 1
| |
h
|
a
|
b
|
hsoft
|
C
|
g
|
ak
|
w
|
|
Mega-column (Flexural)
|
0.03
|
1.12
|
1
|
-0.007
|
45
|
1.1
|
0.4
|
0.02
|
|
Core tube (Flexural)
|
0.08
|
1.4
|
1
|
-0.001
|
100
|
0.7
|
0.55
|
0.1
|
|
Coupling beam (Shear)
|
0.014
|
1.085
|
1
|
-0.07
|
12
|
0.9
|
0.4
|
0.5
|
|
Outrigger (Shear)
|
0.04
|
1.15
|
1
|
-0.05
|
150
|
0.6
|
0.4
|
-0.1
|
|
Outrigger (Flexural)
|
0.05
|
1.2
|
1
|
-0.001
|
15
|
0.6
|
0.001
|
-0.1
|
|