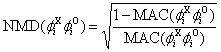|
Acknowledgements
The authors are grateful for the financial
support received from the National Nature Science Foundation of China (No.
51222804, 91315301), the Beijing Natural Science Foundation (No. 8142024)
and the Fok Ying Dong Education Foundation (No. 131071).
References
ATC. Soil-structure interaction for building
structures (ATC 84). Applied Technology Council, Redwood City, California, 2012.
Avil¨¦s J, P¨¦rez-Rocha L E. Soil-structure interaction
in yielding systems. Earthquake Engineering & Structural Dynamics, 2003,
32(11): 1749-1771.
Banerjee S, Lee F H. Centrifuge shaking table tests on
a single pile embedded in clay subjected to earthquake excitation. International
Journal of Geotechnical Engineering, 2013, 7(2): 117-123.
Chaallal O, Ghlamallah N.
Seismic response of flexibly supported coupled shear walls. Journal of Structural
Engineering, 1996, 122(10): 1187-1197.
Chang B J, Raychowdhury P, Hutchinson
T C, Thomas J M, Gajan S, Kutter B L. Evaluation of the seismic performance
of combined frame-wall-foundation structural systems through centrifuge testing.
Proceedings of the 4th International Conference on Earthquake Geotechnical
Engineering. Thessaloniki, Greece, Paper No. 1497, June 25-28, 2007.
Chen W H, Lu Z R, Chen S H,
Ni Y Q, Liao W Y. Monitoring dynamic characteristics of Canton Tower under
different excitations. Journal of Vibration and Shock, 2012, 32(3): 49-54. (in Chinese)
China Institute of Building
Standard Design & Research. Specification for design of steel-concrete
mixed structure of tall buildings (CECS 230: 2008). China Planning Press,
Beijing, China, 2008. (in Chinese)
Ciampoli M, Pinto P E. Effects of soil-structure interaction
on inelastic seismic response of bridge piers. Journal of Structural Engineering, 1995, 121(5): 806-814.
Deng L, Kutter B L, Kunnath
S. Centrifuge modeling of bridge systems designed for rocking foundations.
ASCE Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(3):
335-344.
Drosos V, Georgarakos T, Loli
M, Anastasopoulos I, Zarzouras O, Gazetas G. Soil-foundation-structure interaction
with mobilization of bearing capacity: An experimental study on sand. ASCE
Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(11): 1369-1386.
Farghaly A A, Ahmed H H. Contribution
of soil-structure interaction to seismic response of buildings. KSCE Journal
of Civil Engineering, 2013, 17(5): 959-971.
Gao X W, Bu Q S. Rational
factor of cycle reduction and inter-story elastic drift correction for multi-story
RC-frame building. Building Structure, 1993, 17(2): 42-46. (in Chinese)
Gazetas G, Mylonakis G. Seismic soil-structure interaction:
new evidence and emerging issues. In: ASCE. Geotechnical Earthquake Engineering
and Soil Dynamics III, vol. 2. Reston, Virginia: Geotechnical Special Publication,
1998: 1119-1174.
Han Y. Seismic response of
tall building considering soil-pile-structure interaction. Earthquake Engineering
and Engineering Vibration, 2002, 1(1): 57-64.
Jarernprasert S, Bazan-Zurita E, Bielak J. Seismic soil-structure
interaction response of inelastic structures. Soil Dynamics and Earthquake
Engineering, 2013, 47: 132-143.
Jiang X L, Li B Q, Lao H Y.
Seismic response analysis of pile-soil-structure of the Shanghai Tower¡¯s Miranda
model. Earthquake Resistant Engineering and Retrofitting, 2013, 35(4): 42-47.
(in Chinese)
Li W Y. China: A country locked in fierce competition
to build super high-rises. Time + Architecture, 2011, 28(3): 9. (in Chinese)
Li Z Q. Research on structure
health monitoring of Jin Mao Tower. PhD thesis, Tongji University, China,
2007.
(in Chinese)
Liu W, Hutchinson T C, Kutter B L, Hakhamaneshi
M, Aschheim M, Kunnath S. Demonstration of compatible yielding between soil-foundation
and superstructure components. Journal of Structural Engineering, ASCE, 2012, 139: 1408-1420.
Lu X L, Chen Y Q, Chen B,
Huang W, Zhao L. Shaking table testing of dynamic soil-structure interaction
system. Journal of Earthquake Engineering and Engineering Vibration, 2000,
20(4): 20-29. (in Chinese)
Lu X L, Li P Z, Guo X Q, Shi
W X, Liu J. Vibration control and site measurement on Shanghai World Financial
Center Tower. Structural Engineers, 2009, 25(4): 63-70. (in Chinese)
Lu X L, Shi W X, Shen J H,
Fan P F. Measurement on dynamic property of several super high-rise buildings
in Shanghai. Building Science, 2001, 17(2): 36-39. (in Chinese)
Lu X, Chen B, Li P Z, Chen
Y Q. Numerical analysis of tall buildings considering dynamic soil-structure
interaction. Journal of Asian Architecture and Building Engineering, 2003,
2(1): 1-8.
Lu X, Lu X Z, Zhang W K, Ye
L P. Collapse simulation of a super high-rise building subjected to extremely
strong earthquakes. Science China Technological Sciences, 2011, 54(10): 2549-2560.
Luco J E, Trifunac M D, Wong
H L. Isolation of soil-structure interaction effects by full-scale forced
vibration tests. Earthquake Engineering & Structural Dynamics, 1988, 16(1):
1-21.
Meyerhof G G. Some recent
foundation research and its application to design. The Structural Engineer,
1953, 31(6):151-167.
Ministry of Construction of
the People¡¯s Republic of China. Code for seismic design of buildings (GB50011-2010).
China Architecture & Building Press, Beijing, China, 2010. (in Chinese)
Mylonakis G, Gazetas G. Seismic
soil-structure interaction: beneficial or detrimental? Journal of Earthquake
Engineering, 2000, 4(03): 277-301.
Mylonakis G, Syngros C, Gazetas
G, Tazoh T. The role of soil in the collapse of 18 piers of Hanshin Expressway
in the Kobe earthquake. Earthquake Engineering & Structural Dynamics,
2006, 35(5): 547-575.
Pitilakis D, Clouteau D. Equivalent
linear substructure approximation of soil-foundation-structure interaction:
model presentation and validation. Bulletin of Earthquake Engineering, 2010,
8(2): 257-282.
Ravichandran N, Krishnapillai S, Machmer B. Centrifuge
modeling of unsaturated soil-pile system. Proceeding of GeoCongress 2012:
State of the Art and Practice in Geotechnical Engineering, 2012: 1978-1987.
Stewart J P, Fenves G L, Seed R B. Seismic soil-structure
interaction in buildings. I: Analytical methods. Journal of Geotechnical and
Geoenvironmental Engineering, 1999, 125(1): 26-37.
Vamvatsikos D, Cornell C A.
Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics,
2002, 31(3): 491-514.
Veletsos A S, Meek J W. Dynamic
behaviour of building-foundation systems. Earthquake Engineering & Structural
Dynamics, 1974, 3(2): 121-138.
Wang M W. Dynamic Centrifuge Tests and Numerical Modelling
for Geotechnical Earthquake Engineering in Liquefiable Soils. Science Press,
Beijing, China, 2012. (in Chinese)
Wang X L, Qu W L, Liu H. Finite
element analysis on dynamic characteristics of super high tower in Guangzhou.
Journal of Wuhan University of Technology, 2007, 29(1): 142-144+156. (in Chinese)
Waters T P. Finite element model updating
using measured frequency response functions. PhD thesis, University of Bristol,
U.K., 1995.
Wolf J P. Dynamic soil-structure interaction. N.J.: Prentice-Hall,
Inc., Englewood Cliffs, 1985.
Zhu J J, Lu X L, Zou Y. Shake-table
test and theoretical analysis for Shanghai World Financial Center scale model.
China Civil Engineering Journal, 2005, 38(10): 22-30. (in Chinese)
Zhu J J, Lu X L. Elastoplastic time-history analysis of
Shanghai World Financial Center Building. Journal of Natural Disasters, 2006,
15(2): 49-56. (in Chinese)
List of Tables
Table 1.
Typical comparison of the field test periods
and the laboratory test or numerical simulation periods
Table 2.
Thickness and material properties of each
soil layer in the FE model of the soil-foundation system
Table 3.
Comparison of the first three translational
vibration periods of Shanghai Tower in the x and y direction
Table 4.
Comparison between the translational vibration
modes of Models A, B and C and Model O
Table 5.
Comparison of the failure sequences at the
critical ground motion intensity of El-Centro
List of figures
Fig. 1.
Schematic illustration of analysis methods
of the soil-structure interaction
Fig. 2.
Schematic illustration of the lateral-force-resisting
system of Shanghai Tower (Lu et al., 2011)
Fig. 3.
Three-dimensional FE model of Shanghai Tower
(Lu et al., 2011)
Fig. 4.
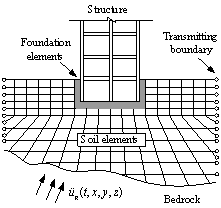
Schematic diagram of the soil-foundation system
of Shanghai Tower
Fig. 5.
Final collapse mode of Model B subjected to
El-Centro in the x direction (PGA=1.7 g)
Fig. 6.
Collapse process of Model B subjected to El-Centro
in the x direction (PGA=1.7 g)
Fig. 7.
Distribution of the horizontal displacement
along the height at the critical collapse state
Fig. 8.
Comparison of the CMR of the four models subjected
to El-Centro in the x direction
Fig. 9.
Roof vertical displacement time histories
at the critical ground motion intensity of El-Centro
Table 1 Typical comparison of the field test
periods and the laboratory test or numerical simulation periods
| |
Height
(m)
|
Period
|
Field test period (s)
|
Laboratory test period (s)
|
d
(%)
|
Numerical simulation period (s)
|
d (%)
|
|
Shanghai World Financial Center (Lu et al., 2009; Zhu and Lu, 2006;
Zhu et al., 2005)
|
492
|
T1
|
6.502
|
5.542
|
-14.76
|
6.500
|
-0.03
|
|
T2
|
6.398
|
5.542
|
-21.74
|
5.800
|
-9.35
|
|
Shanghai Triumphal Arch Building (Lu
et al., 2001)
|
100
|
T1
|
1.795
|
1.577
|
-12.14
|
|
|
|
T2
|
1.383
|
1.082
|
-21.76
|
|
|
|
Shanghai Jin Mao Tower (Li, 2007)
|
420.5
|
T1
|
6.862
|
|
|
5.637
|
-17.85
|
|
T2
|
6.829
|
|
|
5.679
|
-16.84
|
|
Canton Tower (Wang et al., 2007; Chen
et al., 2012)
|
610
|
T1
|
10.68
|
|
|
9.703
|
-9.15
|
|
T2
|
7.191
|
|
|
6.714
|
-6.63
|
Note:
the relative deviation d indicates the difference from the field test period.
Table 2 Thickness and material properties of each soil layer in the
FE model of the soil-foundation system
|
Soil layer
|
Range of depth (m)
|
Density (kN/m3)
|
Poisson ratio
|
Elasticity modulus (MPa)
|
|
1
|
0 ~ -15
|
18.4
|
0.49
|
20.36
|
|
2
|
-15 ~ -30
|
18.15
|
0.47
|
20.55
|
|
3
|
-30 ~ -115
|
23.8
|
0.46
|
74.4
|
|
4
|
-115 ~ -157
|
42.8
|
0.46
|
97.6
|
Table 3 Comparison of the first three translational vibration periods
of Shanghai Tower in the x and y direction
| |
|
Model O
|
Model A
|
Model B
|
Model C
|
| |
|
T (s)
|
T (s)
|
d
|
T (s)
|
d
|
T (s)
|
d
|
|
X Direction
|
1st translational mode
|
9.83
|
13.49
|
37.3%
|
11.79
|
20.0%
|
10.85
|
10.4%
|
|
2nd translational mode
|
3.57
|
3.76
|
5.4%
|
3.70
|
3.6%
|
3.65
|
2.2%
|
|
3rd translational mode
|
1.67
|
1.78
|
6.0%
|
1.74
|
4.1%
|
1.72
|
2.5%
|
|
Y Direction
|
1st translational mode
|
9.77
|
13.45
|
37.7%
|
11.74
|
20.2%
|
10.79
|
10.5%
|
|
2nd translational mode
|
3.52
|
3.71
|
5.5%
|
3.64
|
3.6%
|
3.59
|
2.2%
|
|
3rd translational mode
|
1.66
|
1.76
|
6.3%
|
1.73
|
4.3%
|
1.70
|
2.6%
|
Note:
the relative deviation d indicates the difference from Model O.
Table 4 Comparison between the translational
vibration modes of Models A, B and C and Model O
| |
Mode
|
X Direction
|
Y Direction
|
|
NMD(O-A)
|
1st translational mode
|
7.67%
|
7.68%
|
|
2nd translational mode
|
11.40%
|
11.21%
|
|
3rd translational mode
|
10.00%
|
10.31%
|
|
NMD(O-B)
|
1st translational mode
|
5.05%
|
5.07%
|
|
2nd translational mode
|
7.59%
|
7.50%
|
|
3rd translational mode
|
6.83%
|
7.08%
|
|
NMD(O-C)
|
1st translational mode
|
3.00%
|
3.01%
|
|
2nd translational mode
|
4.54%
|
4.50%
|
|
3rd translational mode
|
4.18%
|
4.34%
|
Table 5 Comparison of the failure sequences at the critical ground
motion intensity of El-Centro
|
Failure sequence
|
Model A
|
Model B
|
Model C
|
Model O
|
|
1
|
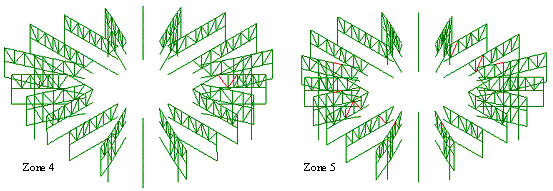
Diagonal members of the outriggers in Zones 4 and 5
begin to yield
|
Diagonal members of the outriggers in Zones 4 and 5
begin to yield
|
Diagonal members of the outriggers in Zones 4 and 5
begin to yield
|
Diagonal members of the outriggers in Zones 4 and 5
begin to yield
|
|
2
|
Shear walls at the bottom of Zone 7 begin to fail
|
Shear walls at the bottom of Zone 7 begin to fail
|
Shear walls at the junction of Zones 4 and 5 are crushed
|
Shear walls at the junction of Zones 4 and 5 are crushed
|
|
3
|
Shear walls at the junction of Zones 4 and 5 are crushed
|
Shear walls at the junction of Zones 4 and 5 are crushed
|
Coupling beams begin to fail
|
Some shear walls at the bottom of Zone 8 begin to fail
|
|
4
|
Coupling beams begin to fail
|
Coupling beams begin to fail
|
Mega-columns at the bottom of zone 5 begin to fail
|
Coupling beams begin to fail
|
|
5
|
Mega-columns at the bottom of Zone 5 begin to fail
|
Mega-columns at the bottom of Zone 5 begin to fail
|
The entire structure begins to collapse
|
Mega-columns at the bottom of Zone 5 begin to fail
|
|
6
|
The entire structure begins to collapse
|
The entire structure begins to collapse
|
|
The entire structure begins to collapse
|
|
|
|
|
(a)
Direct analysis approach
|
(b)
Substructure approach
|
Fig. 1. Schematic illustration of analysis methods of the soil-structure
interaction
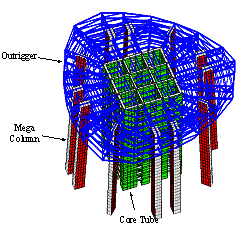
Fig. 2. Schematic illustration of the lateral-force-resisting system
of Shanghai Tower (Lu et al., 2011)
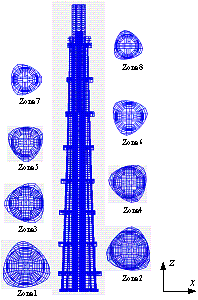
Fig. 3. Three-dimensional FE model of Shanghai Tower (Lu et al., 2011)
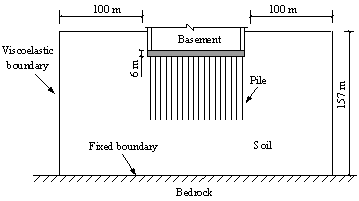
Fig. 4. Schematic diagram of the soil-foundation system of Shanghai
Tower
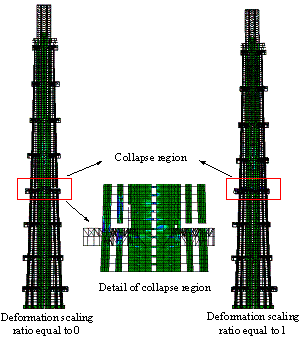
Fig. 5. Final collapse mode of Model B
subjected to El-Centro in the x direction (PGA=1.7 g)
|
|
|
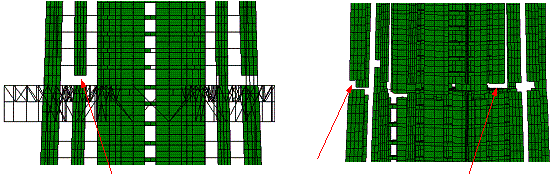
(a) t=1.50 s, diagonal members
of the outriggers in Zones 4 and 5 begin to yield
|
|
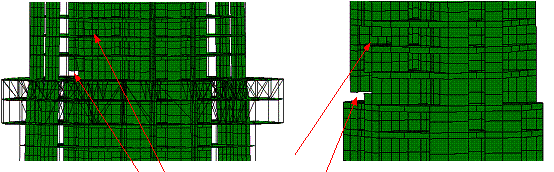
|
|
(b) t=2.60 s, flange walls of the
core tube at the bottom of Zone 7 begin to fail
|
|
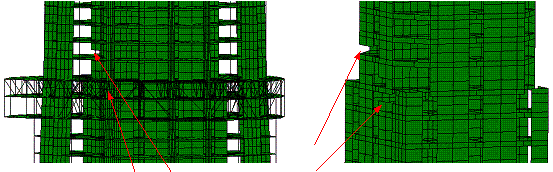
|
|
(c) t=3.43 s, shear walls at the
junction of Zones 4 and 5 are crushed
|
|
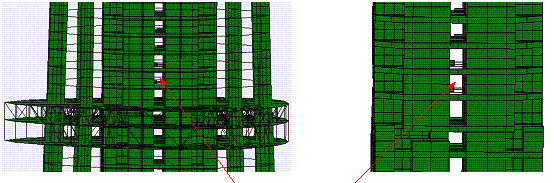
|
|
(d) t=3.58 s, coupling beams along
the x direction in the core tube begin to fail
|
|
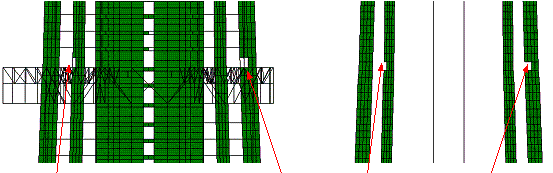
|
|
(e) t=5.83 s, mega-columns at the
bottom of Zone 5 begin to fail
|
|
|
|
(f) t=6.28 s, the entire structure
begins to collapse
|
Fig. 6. Collapse process of Model B subjected
to El-Centro in the x direction (PGA=1.7 g)
|
|
|
|
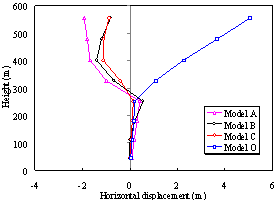
(a) Distribution of horizontal displacement
|
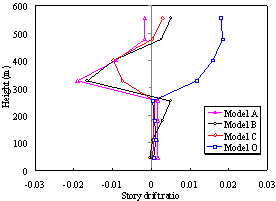
(b) Distribution
of drift ratio in each zone
|
Fig. 7. Distribution of the horizontal displacement
along the height at the critical collapse state
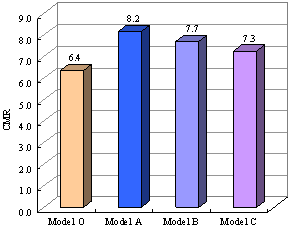
Fig. 8. Comparison of the CMR of the four
models subjected to El-Centro in the x direction
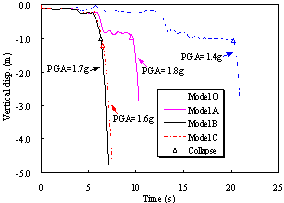
Fig. 9. Roof vertical
displacement time histories at the critical ground motion intensity of El-Centro
|