New Analytical Calculation Models for Compressive Arch Action in Reinforced Concrete Structures

1 Introduction

Progressive collapse study has become an important research frontier since the collapse of Alfred P. Murrah Federal Building in the 1995 Oklahoma City bombing attack [1]. Current research outcomes indicate that a structure can resist the progressive collapse through two major mechanisms, i.e., the beam mechanism at small deformations and the catenary mechanism at large deformations [2-10]. As such, fully utilizing these two resistance mechanisms has become the primary objective of the current progressive collapse design codes [11-12]. According to the existing experimental observations, compressive arch action (CAA) is commonly found in reinforced concrete (RC) beams at small deformations [5-10, 13-19]. Quantitatively, CAA has been found to improve the structural resistance by 30% to 150% as indicated in the existing studies [10, 14]. Therefore, an accurate and easy-to-use calculation model for CAA is of significant value for achieving a rational progressive collapse design.

An illustration of CAA is shown in Figure 1, where the middle column fails and loses its load carrying capacity. The unbalanced gravity load from the structure above, which is originally carried by the failed column, is subsequently transformed into a concentrated load P on the beam-column joint. At the early stage of loading, the structural resistance to progressive collapse is provided by the flexural capacities (i.e., M₁ & M₂) of the frame beams (Figure 1a). As the displacement increases, cracking of the concrete will cause a migration of the neutral axis, accompanied by an in-plane expansion of the specimen. When this expansion is restrained by the boundaries at the beam ends, CAA will be formed in the beams which will in turn enhance the strength of the specimens as shown in Figure 1b [20].

(a)      Resistance mechanism of RC beams at initial loading stage

(b)      Resistance mechanism of RC beams at CAA stage

Figure 1 CAA in RC beams at small deformation stage under concentrated load

(Note: 1, 2, 3, 4 denote various beam sections)

Many theoretical investigations have been performed to evaluate the CAA resistance, among which Park & Gamble proposed one of the most widely accepted CAA calculation model [21]. The Park & Gamble’s model was validated by Su et al. [14] and Qian et al. [10] with their experimental tests. Afterwards, Yu & Tan [22] and Kang & Tan [23] further updated the Park & Gamble’s model, by calculating iteratively the force-displacement relationship of RC beams at the CAA stage. The existing literature shows that the computational models of Park & Gamble [21], Yu & Tan [22] and Kang & Tan [23] are sufficiently accurate when calculating the CAA resistance of RC frame beams. However, further studies are still required due to the following reasons:

(1)    The abovementioned models are not suitable for practical use in progressive collapse design: (a) the Park & Gamble’s model [21] requires the peak displacement of the CAA, which cannot be easily obtained for real structures; (b) the models proposed by Yu & Tan [22] and Kang & Tan [23] require iterative calculations of the relative depth of the equivalent compression zone, making the associated computation infeasible without dedicated computer programming.

(2)    In real RC frame structures, the frame beams and slabs are always cast together to carry the dead and live loads. According to Ren et al. [7] and Lu et al. [8], the presence of slab can significantly improve the progressive collapse resistance at the CAA stage. However, existing models can only calculate the CAA of frame beams. In the presence of slabs, reinforcing steels on beam sections 1 to 4 (Figure 1b) do not yield simultaneously, which violates the fundamental assumptions of the existing models. Hence, when these models are used for evaluating the CAA resistance of the frame beams with the slab effect, significant errors would be expected.

In this study, we simplified the boundary conditions as fixed ends in order to provide an explicit solution for calculating the CAA resistance of RC beams under interior column removal scenarios. Such simplification also helped to simplify the prediction equations, making the proposed model more practical and feasible for practical engineering applications. Note that in the alternate path (AP) design method as specified in most of the existing progressive collapse design codes [11-12], a column removal means removing the clear height of the selected column between the lateral restraints at both column ends. In real situations, the interior beams or beam-slab substructures are always surrounded by the peripheral structural components (i.e., beams, columns and slabs of the adjacent bays). These components will provide sufficient restraints to the deformation of the boundaries. It is therefore rational to assume such fixed boundaries when considering the interior column removal case in an RC structure.

To overcome the limitations of the existing calculation models for CAA, we established a series of finite element (FE) models fully validated against a large database of experimental outcomes. For both beam and beam-slab specimens, their sectional stress-strain distributions, key design parameters and the corresponding sensitivities were analyzed using the validated FE models. Following the experimental and numerical analysis, we proposed explicit and easy-to-use CAA calculation models for RC beams with and without slabs. Comparison with the published experimental results of other researchers confirms that the newly developed models can accurately produce the progressive collapse resistance of RC beams (with and without slabs) at the CAA stage. The computational procedure of the new models is simple and easy to implement. The findings from this study can serve to provide a quantitative reference for practical design of RC frame structures against progressive collapse.

2 Validation of the Park & Gamble’s model

2.1 The Park & Gamble’s Model

The Park & Gamble’s model [21] is based on the deformation compatibility and force equilibrium of RC beams under a concentrated load (Figure 2a). Considering the isolated beam model shown in Figure 2b, the progressive collapse resistance (P) at CAA stage can be expressed as:

where d is the peak displacement corresponding to the peak load; M₁ and M₂ are the moments at the beam ends; N is the axial force induced by CAA; l is the total length of the two-span beam; b is the ratio between the net span and the total span l. Note that M₁, M₂ and N can be derived by calculating the resultant forces at the corresponding cross sections.

(a)    Axially restrained two-span RC frame beam under concentrated load

(b)    Free-body diagram between Sections 1 and 2

Figure 2 The Park & Gamble’s model (Note: 1, 2, 3, 4 denote various beam sections)

In the Park & Gamble’s model, the relative depths of the compression zones at Sections 1 and 2 are obtained by solving the equations of deformation compatibility and force equilibrium:

where  and c are the relative depth of the compression zone at Sections 1 and 2, respectively; h and b are the height and width of the beam, respectively; is the axial compressive strain of the beam; t is the longitudinal movement of the boundary; and  are the resultant forces in concrete at Sections 1 and 2;  and T are the tensile forces in reinforcement at Sections 1 and 2, respectively;  and  are the compressive forces in reinforcement at Sections 1 and 2, respectively; f_c' is the concrete cylinder strength; is the ratio of the depth of the equivalent rectangular stress block to the depth of neutral-axis, as defined in ACI 318-14 [24].

In order to calculate the force contributions from concrete and reinforcement, it was assumed by Park & Gamble that the critical sections have reached their strengths when a full plasticity is developed at the critical sections of the beam (i.e., the peak point at the CAA stage) [21]. Note that under certain circumstances, the above assumption may not be very valid as the compressive reinforcement at Section 2 may not yield at the peak point of CAA. However, since the Park & Gamble’s model has been proven to be able to provide accurate predictions of the load carrying capacities of RC beams under CAA [10, 14, 21], this assumption is nonetheless adopted in the calculation procedure of the RC beam specimens for its simplicity. Hence, the moments M₁, M₂ and the axial force N can be calculated by combining Equations 2 and 3 with the stress-strain relationships of the reinforcement and concrete at the ultimate state, after which the CAA resistance P of the RC beams can then be readily calculated following Equation 1. The expressions of M₁, M₂ and N at the beam ends are obtained as:

where d' is the thickness of the concrete cover.

2.2 The database of experimental tests

Many experiments have been reported to study progressive collapse of RC frame beams under different column removal scenarios. In order to validate the calculation models for CAA, a total of 50 RC progressive collapse specimens, tested by other researchers under a mid-column removal scenario, were collected from the literature. Details of these RC specimens are listed in Appendix A [5-7, 10, 13-17, 25-26], in which 45 are beam specimens and 5 are beam-slab specimens. In addition to the test specimens included in Appendix A, we also reviewed a number of other RC progressive collapse tests found in the literature (e.g., Lu et al. [8], Qian et al. [10], Choi & Kim [18], Sadek et al. [19], Qian & Li [27], Prasad & Hutchinson [28], and Dat & Tan [29]). However, comparing to the illustrations shown in Figures 1 and 2, these additional tests typically have different boundary conditions or deformation modes, and hence they are not considered in this work.

2.3 Validation of the Park & Gamble’s model

Following the Park & Gamble’s model [21], the CAA resistance P is computed for all 45 beam specimens given in Appendix A, and the calculated results are compared with the corresponding experimental measurements. Note that the Park & Gamble’s model requires the displacement d at the peak resistance of CAA, for which the experimentally measured values are adopted in the calculation. The comparisons are shown in Figure 3a, where the mean absolute error (MAE) is 10.97% with a standard deviation of 0.128. This confirms that given the peak displacement d corresponding to the peak resistance of CAA, the Park & Gamble’s model is sufficiently accurate in calculating the CAA resistance P.

(a) Results obtained with experimentally measured d	(b) Results obtained with d=0.5h

Figure 3 Calculated CAA resistance from the Park & Gamble’s model
versus experimental results

However, for real-world structures, it is often hard, if not impossible, to obtain the d value through experiments, making the Park & Gamble’s model impractical in engineering practice. To resolve this situation, Park & Gamble [21] recommended  for use in their calculation procedure. The CAA resistances calculated using the assumption  are shown in Figure 3b, where the MAE is 20.47% with a standard deviation of 0.158. This suggests that the prediction obtained with  significantly underestimates the CAA resistance, and the reduced prediction accuracy poses a major constraint to the practical use of the Park & Gamble’s model.

3 The FE model

Finite element analyses of the 50 RC beam and beam-slab test specimens were conducted to predict their CAA resistances under the mid-column removal scenario based on OpenSees [30]. The fiber-beam element was adopted in these FE analyses, since its feasibility and accuracy in simulating progressive collapse of RC beams have been confirmed in many previous research works [2-4, 31-35]. The FE model of every test specimen shared the similar modeling strategies in OpenSees. Specifically, displacement-based beam-column elements were used to model the RC beams. Five Gauss integration points were considered along each element. The beam section was defined using the fiber section in OpenSees. Reinforcement fibers were arranged at the exact positions as those in the test specimens according to the drawings provided in the literature. Concrete01 Material and Steel02 Material with 2% strain hardening were used to model the concrete and reinforcing steel, respectively, in OpenSees [33]. Among the existing experimental studies, very limited data could be found to quantify the bar-slip behaviors within the beams. As such, the bar-slip behavior between the reinforcement and the concrete were simulated by reducing the elastic stiffness of the reinforcement [36]. Moreover, in most of the relevant experimental tests, column stubs are always considered to remain at the column removal location of the specimen as specified in the AP method in DoD 2016 [12]. Such column stubs, containing much more reinforcement than the beams, often deform elastically during the tests. Hence, the mid beam-column joints in the FE models were modeled using elastic beam-column elements in OpenSees.

Typically, the load-displacement relationships obtained through the FE analyses of Specimens B1 [6] and S6 [7] are plotted in Figures 4a and 4b, respectively, where the blue lines indicate the FE results and the red lines denote the experimental measurements. For all 45 beam specimens and 5 beam-slab specimens listed in Appendix A, the numerically predicted CAA resistances are compared with the experimental measurements in Figure 4c, where the MAE is found to be 8.34% with a standard deviation of 0.097. It is evident that the accuracy of the present FE model is better than that of the Park & Gamble’s model, which justifies the use of this FE model to carry out comprehensive parametric studies presented for both beam and beam-slab specimens in the subsequent sections.

(a)    Load versus displacement for Specimen B1 [6]	(b)    Load versus displacement for Specimen S6 [7]
(c)    Numerical versus experimental CAA resistance for all specimens

Figure 4 Validation of the FE models

Moreover, based on the above FE models, a parametric study is conducted to evaluate the influence of the boundary stiffness on the peak resistance of an RC beam under CAA. Two indexes (i.e., R_a and R_r) proposed by Yu & Tan [37] are adopted, of which, R_a is defined as the ratio between the axial stiffness of the boundary and the EA/l of the RC beam, and R_r is the ratio between the rotational stiffness of the boundary and the EI/l of the RC beam. The results indicate that the boundary of an RC beam can be assumed as fixed ends when R_a is greater than 2 and R_r is greater than 10.

4 The new CAA calculation model for beam specimens

As discussed in Sections 2, the practical application of the Park & Gamble’s model relies on an erroneous and oversimplified assumption of the peak displacement , which introduces significant error to the CAA resistance prediction and limits the usefulness of the model. Through the FE parametric study, we aim to find a better way to evaluate the d value, and significantly improve the prediction accuracy of the Park & Gamble’s model.

According to the FE results of the 45 beam specimens, three factors are found to affect the value of d: (1) beam length l (2) beam height h and (3) concrete cylinder strength f_c'. Specimen B1 (Figure 4a) tested by Chu et al. [6] was taken as a prototype to study these key influencing factors. The values of l, h and f_c' are varied one at a time in the FE model of Specimen B1 within the range of 1 m ≤ l ≤ 8 m, 0.1 m ≤h ≤ 0.5 m and 10 MPa ≤ f_c' ≤ 50 MPa, respectively. The results of the parametric study are presented in Figure 5.

(a) d-l relationship	(b) d-h relationship
(c) d-fc' relationship

Figure 5 Parametric study of the peak CAA displacement

It is evident from the parametric study that d is approximately proportional to l², inversely proportional to h, and linearly reduced with the increase of f_c'. Note that the influence of f_c' can be neglected compared to that of l² and h. Therefore, l²/h is adopted in this study to predict d. Note that with respect to the units, the term l²/h also results in a rational unit for predicting the peak displacement. For the aforementioned 45 beam specimens, the values of d and l²/h due to the validated FE model are collated and regressed in Figure 6a. The regression result indicates that d can be estimated by l²/h with a satisfactory correlation coefficient (i.e., R²=0.9459). The equation for d from the regression is thus:

			(7)
(a) d~l2/h relationship	(b) Comparison with the experimental results

Figure 6 Validation of the proposed model for CAA calculation of RC beam specimens

In the proposed equation (Equation 7) estimating δ, the influence of the beam stiffness is considered automatically. For a unit width of the reinforced concrete beam, both the flexural stiffness and axial stiffness are determined by three parameters: (1) the elastic modulus, E; (2) the length of the beam specimen, l; (3) the height of the beam cross section, h. Note that for most of the RC beams in engineering practice, the elastic modulus is mainly determined by the Young’s modulus of the concrete (E_c), which is related to the compressive strength of concrete. Figure 5c shows that the compressive strength of concrete has limited influence on δ. Hence, only the length (l) and height (h) of the beam are used to express the peak displacement (δ) from the regression analysis and the stiffness of the beam is considered implicitly in Equation 7.

Substituting Equation 7 into Equations 1-6, the CAA resistance of RC beams can be predicted. The calculation results are compared with the experimental ones in Figure 6b, where the MAE is 8.85% with a standard deviation of 0.109. More detailed results, including the calculated peak resistances and corresponding boundary axial forces, can also be found in Table A.1 in Appendix A. For the CAA, quantification of the peak axial force could help gain a better understanding of the collapse mechanisms of RC structures. It should be noted, however, that the boundary axial force of an RC substructure under CAA is very sensitive to the actual boundary stiffness. Moreover, as indicated by many existing experimental and analytical results [5, 10, 14, 17, 22], the boundary axial force may not reach the peak value when the RC beam reaches the peak resistance under CAA. Notwithstanding, further studies are required to evaluate the axial force in an RC beam under CAA.

The results indicate that the proposed model provides a much more accurate prediction of the CAA resistance of an RC beam compared to the prediction using the oversimplified assumption . Compared to the iterative models proposed by Yu & Tan [22] and Kang & Tan [23], the proposed new model is explicit and completely avoids the time-consuming iterations, making it more practical and feasible for engineering applications. In addition, as d in Equation 7 is estimated based on the FE parametric study, the uncertainties associated with the experimental measurement of d can be eliminated, leading to even smaller errors in predictions from the proposed model than the original Park & Gamble’s model (Figure 3a).

5 The new CAA calculation model for RC beam-slab specimens

As reviewed earlier in Section 1, a major weakness of the Park & Gamble’s model is the negligence of the slab effects. In real structures, the slab is normally cast together with the underneath beams, and it can provide additional resistance to progressive collapse of the structure. The interaction between the beam and the slab and its effect on the CAA resistance can be examined through experimental tests and numerical analyses of the beam-slab specimens. For a beam-slab specimen, the sectional stress-strain distributions of both reinforcement and concrete are more complicated than those of a beam specimen. Figure 7a shows the free-body diagram of the symmetrical half of the beam-slab substructure, while the internal forces at Sections 1 and 2 are illustrated in Figure 7b. The notations in Figure 7 are explained in Table 1. Compared with the beam specimens, the major differences in the beam-slab specimens are:

Table 1 Description of notations in Figure 7

(1)      The beam-slab specimen has a T-shaped cross section instead of a rectangular one.

(2)      Due to the slab reinforcement, over-reinforced failure occurs at Sections 1 and 4 (i.e., the concrete reaches the crush strain before the tensile reinforcement yields) [7]. On the contrary, at Sections 2 and 3, the tensile reinforcement yields at the early stage of the loading procedure but the compressive reinforcement might not yield at the peak resistance of CAA. The assumption in the Park & Gamble’s model that both concrete and reinforcement reach their ultimate state is no longer applicable for a beam-slab specimen. As a result, the forces M₁, M₂ and N at the beam ends in Equation 1 cannot be directly calculated.

(3)      For the reasons given in (1) and (2) above, the proposed model for predicting the peak displacement d of CAA, i.e. Equation 7, although being very accurate for the regular beam specimen, is not suitable for the T-shaped beam-slab specimen.

(a) Symmetrical half of the beam-slab specimen

(b) Force distribution at typical sections

Figure 7 Diagram of the beam-slab specimen at CAA stage

In order to provide a preliminary view on the limitation of the Park & Gamble’s model (which assumes yielding of all reinforcements), we directly applied the standard calculation procedure of their model to the beam-slab specimens (S2 to S6) tested by Ren et al. [7] and compared the peak resistance predictions with the experimental measurements. As shown in Figure 8, the MAE is 20.40%, and for four fifths of the specimens the errors exceed 20%, which makes the Park & Gamble’s model unfeasible for the beam-slab specimens.

Figure 8 Comparison between the experimental results and the Park & Gamble’s model for beam-slab specimens

5.1 Parametric study of beam-slab specimens using validated FE model

The validation described in Section 3 has proved that the proposed FE model is capable of simulating the behavior of beam-slab specimens at the CAA stage with a good accuracy. Due to the limited number of the beam-slab experiments in the literature, we performed a comprehensive parametric study of the beam-slab specimens using the validated FE model, where a series of RC beam-slab substructures with commonly used dimensions were designed according to the Chinese Code for the Design of Concrete Structures [38]. The design parameters of these beam-slab substructures are listed in Table 2. The 6-story and 4-bay RC frame used by Ren et al. [7], Lu et al. [8] and Lin et al. [32] is taken as the prototype building. The dead load and live load on the floor are 5.0 kN/m² and 2.0 kN/m², respectively. For each individual design, only one design parameter is varied according to the values given in Table 2. In total, 217 models (designated as model number 1 to 217) with different span lengths, beam heights, beam widths, slab thicknesses and slab widths are derived based on the MOHURD 2010 code [38] and analyzed using the validated FE model.

Table 2 Design parameters of different beam-slab substructures

5.2 Analysis of typical cross sections

For all 217 beam-slab substructures, Sections 1 and 2 are chosen as the typical cross sections as shown in Figure 7b. According to the previous analysis, at the point of peak CAA resistance: (1) the bottom beam reinforcement at Section 1 yields under compression, while the depth of the compressive zone of concrete, the resultant forces of the slab reinforcement and the top beam reinforcement are unknown; (2) the bottom beam reinforcement at Section 2 yields under tension, while the depth of the concrete compressive zone, the resultant forces of the slab reinforcement and the top beam reinforcement are also unknown. Hence, to calculate the CAA resistance of the beam-slab substructures, the following parameters need to be specified:

(1)      Parameters for Section 1:

(a)      The depth of the concrete compressive zone in the slab (i.e., s). Note that s < 0 indicates that the concrete compressive zone locates only at the beam web section.

(b)      The tensile force of the bottom slab reinforcement (i.e., T'_SSB).

(c)      The tensile forces of the top slab and the top beam reinforcements (i.e., T'_SST and T'_SBT). For simplicity, it is assumed that the top slab and the top beam reinforcements are at the same height. Assuming that the plane sections remain plane, the strains of the top slab and the top beam reinforcement also remain the same.

(2)      Parameters for Section 2:

(a)      The depth of the concrete compressive zone in the slab (i.e., c). Note that c> h_f indicates that part of the concrete compressive zone locates at the beam web section.

(b)      The tensile force of the bottom slab reinforcement (i.e., T_SSB).

(c)      The compressive forces of the top slab and the top beam reinforcements (i.e., C_SST and C_SBT). Assuming that the plane sections remain plane, the strains of the top slab and the top beam reinforcements also remain the same.

Let s_s = k_if_y denote the stress levels of the reinforcement at different sections, where k_i is the reinforcement stress coefficient at Section i and f_y is the yield stress of the reinforcement. The stresses of the reinforcement at Sections 1 and 2 of the 217 beam-slab FE models at the peak resistance of CAA are shown in Figure 9.

(a) Reinforcement stress levels at Section 1

(b) Reinforcement stress levels at Section 2

Figure 9 Stress levels of reinforcement at Sections 1 and 2 of the beam-slab FE models

The FE results indicate that the bottom beam reinforcement yields under compression at Section 1 when the beam-slab substructures reach their peak CAA resistance. The top slab reinforcement yields under tension, while the yielding status of the bottom slab reinforcement depends on the ratio between the area of the upper slab and the underneath beam (i.e., b_bh_b/b_fh_f). The relation between s_s/ f_y and b_bh_b/b_fh_f is shown in Figure 10a (s_s is the stress of the reinforcement), from which the following equations can be derived:

Similarly, for Section 2, the following equations can be derived from Figure 10b:

(a) Section 1

(b) Section 2

Figure 10 Approximation for stress level of the reinforcement

In order to calculate the resultant moments and axial forces at the beam ends, the depths of the concrete compressive zone (i.e., c and s) need to be specified. For the axially restrained beam-slab substructures with fixed boundaries as shown in Figure 7a, the following relation can be derived through deformation compatibility of the beams:

Equation 11 can also be re-written as:

According to the cross sectional equilibrium illustrated in Figure 7b:

The reinforcement stress analyses (Figure 9a) indicates that in most cases the bottom slab reinforcement at Section 1 is under compression, which implies that the concrete at the beam web is also under compression. Therefore, according to Figure 7 and ACI 318-14 [24], it can be derived that:

Substituting Equation 14 into Equation 12 yields:

Based on the above, the resultant force of the reinforcement can be written as:

For Section 1:

For Section 2:

where f_y and A are the yield stress and the reinforcement area, respectively.

Equation 15 can also be re-written as:

The heights of the concrete compression zone at different sections can then be obtained by combining Equations 12 and 18:

Substituting s and c into the following equations gives the concrete resultant compressive forces at Sections 1 and 2:

As both concrete and reinforcement forces are specified, the resultant forces at Sections 1 and 2 (N, M₁ and M₂) can be calculated as:

Finally, the progressive collapse resistance of the beam-slab substructures at the CAA stage can be determined by substituting N, M₁ and M₂ into Equation 1.

5.3 Predicting the peak displacement of CAA for beam-slab substructures

Similar to the calculation procedure for RC beams, the calculation of beam-slab substructures also requires the peak displacement (i.e., d) of CAA in Equation 1 to be determined. Following a similar regression analysis presented in Figures 5 and 6, the geometries of all 217 beam-slab models are used to regress d and the following equation is obtained:

where h_b, b_b, b_f and h_f are defined as in Table1, and l is the total span of the two-span beam. As shown in Figure 11, a good agreement is observed between the predicted d due to Equation 26 and the FE results.

Figure 11 Comparison of the predicted d by Equation 26 and the FE results

5.4 Validation of the accuracy of the proposed model

Based on the d values predicted by Equation 26, the calculation procedure presented in Section 5.2 (i.e., Equations 19 to 25) can be followed to calculate the CAA resistance of the beam-slab specimens tested by Ren et al. [7]. Specimens S6 is taken as an example to illustrate the calculation procedure of the proposed model, and the details of which are provided in Appendix B. For all 217 beam-slab substructures designed in this study, the comparison between the proposed model and the FE results is provided in Figure 12a, where the MAE of prediction is 6.25% with a standard deviation of 0.064. For the five one-way beam-slab specimens (S2 to S6) tested by Ren et al. [7], the calculation results of the proposed model are also compared with the FE and experimental results in Figure 12b, where the MAE of prediction error is 9.46%. More detailed results, including the calculated peak resistances and the corresponding boundary axial forces of the five beam-slab specimens, can also be found in Table A.2 in Appendix A. These comparisons confirm that the proposed explicit model is able to obtain accurately the CAA resistance of the beam-slab specimens.

(a)      Comparison with FE results	(b)      Comparison with the experimental tests by Ren et al. (2016) [7]

Figure 12 Validation of the proposed model beam-slab specimens

6 Conclusion

Compressive arch action serves as a major mechanism to resist progressive collapse in RC frames at the small deformation stage. An accurate and efficient model to calculate the CAA resistance has significant value to the progressive collapse design of RC structures. Existing prediction models can neither meet the engineering practice demands, nor calculate the CAA resistance of the beam-slab specimens. Based on an experimental database of 45 beam specimens and 5 beam-slab specimens, and the FE analyses of 45 beam specimens and 217 beam-slab substructures, explicit and practical calculation models for CAA for RC beams with and without slabs are proposed in this study. The main conclusions are:

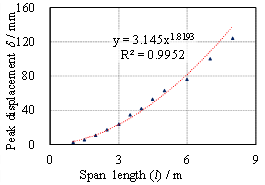
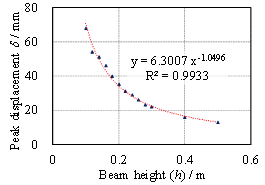
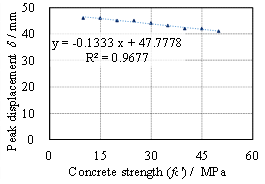
(1)    This study proposes a simple and explicit model capable of calculating the CAA resistance of RC beams based solely on the geometric and reinforcement information. The equations to predict the peak displacement of CAA is proposed based on the regression of the FE results of 45 specimens tested by other researchers. More importantly, the proposed model can be easily mastered by practicing engineers in designing RC structures against progressive collapse.

(2)    A set of 217 beam-slab substructures are designed within the most practically used ranges of span length, beam height, beam width, slab thickness and slab width. The sectional stresses of concrete and reinforcement of the beam-slab substructures under CAA are proposed based on the FE results of these beam-slab substructures. The outcome of this study can help researchers gain a better understanding of the CAA in RC structures when considering the slab effects. Moreover, these results provide a foundation for developing the calculation model for CAA for the beam-slab substructures.

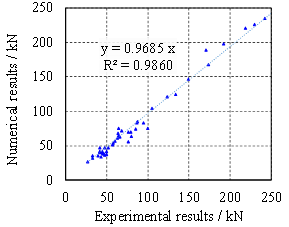
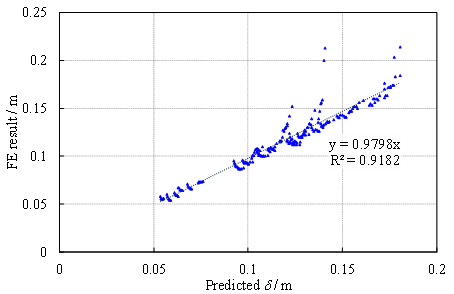
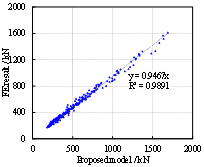
(3)    The explicit CAA resistance calculation model, as well as the corresponding peak displacement prediction method, for beam-slab substructures is proposed. Comparisons with both the FE and experimental results confirm that the proposed explicit model is able to accurately calculate the CAA resistance of RC beam-slab substructures.

It should be noted that the proposed model is developed based on the assumptions of fixed boundary conditions at both beam ends. It should also be recognized that a flexible boundary can notably influence the progressive collapse resistance of RC structures. Future studies are therefore needed to investigate such boundary effects, based on the outcomes of the present study. Correspondingly, the proposed d prediction method and resistance calculation model should also be updated in order to take into account different boundary conditions.

Acknowledgement

The authors are grateful for the financial support received from the National Natural Science Foundation of China (No. 51778341), and the European Community's Seventh Framework Programme (Marie Curie International Research Staff Exchange Scheme, Grant No. 612607).

References

[1]      Sozen M, Thornton C, Corley W, Sr P. The Oklahoma City Bombing: structure and mechanisms of the Murrah Building. J Perform Constr Facil 1998; 12(3): 120-136.

[2]      Li Y, Lu XZ, Guan H, Ye LP. An improved tie force method for progressive collapse resistance design of reinforced concrete frame structures. Eng Struct 2011; 33(10): 2931-2942.

[3]      Li Y, Lu XZ, Guan H, Ye LP. An energy-based assessment on dynamic amplification factor for linear static analysis in progressive collapse design of ductile RC frame structures, Adv Struct Eng 2014; 17(8): 1217-1225.

[4]      Li Y, Lu XZ, Guan H, Ye LP. Progressive collapse resistance demand of RC frames under catenary mechanism. ACI Struct J 2014; 111 (5): 1225-1234.

[5]      Yu J, Tan KH. Structural behavior of RC beam-column sub-assemblages under a middle column removal scenario. J Struct Eng 2012; 139(2): 233-250.

[6]      Chu MJ, Zhou YL, Lu XZ, Li Y. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse. China Civil Engineering Journal 2016; 49(2): 31-40. (in Chinese)

[7]      Ren PQ, Li Y, Lu XZ, Guan H, Zhou YL. Experimental investigation of progressive collapse resistance of one-way reinforced concrete beam-slab substructures under a middle-column-removal scenario. Eng Struct 2016; 118: 28-40.

[8]      Lu XZ, Lin KQ, Li Y, Guan H, Ren PQ, Zhou YL. Experimental investigation of RC beam-slab substructures against progressive collapse subject to an edge-column-removal scenario. Eng Struct 2017; 149: 91-103.

[9]      Yi WJ, He QF, Xiao Y, Kunnath SK. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures. ACI Struct J 2008; 105(4): 433-439.

[10]  Qian K, Li B, Ma JX. Load-carrying mechanism to resist progressive collapse of RC buildings. J Struct Eng 2015; 141(2): 04014107.

[11]  General Services Administration (GSA). Alternate path analysis and design guidelines for progressive collapse resistance. Washington, DC. 2016.

[12]  Department of Defense (DoD). Design of structures to resist progressive collapse. Unified facility criteria, UFC 4-023-03, Washington, DC. 2016.

[13]  Yu J, Tan KH. Special detailing techniques to improve structural resistance against progressive collapse. J Struct Eng 2013; 140(3): 04013077.

[14]  Su YP, Tian Y, Song X. Progressive collapse resistance of axially-restrained frame beams. ACI Struct J 2009; 106(5): 600-607.

[15]  Sasani M, Werner A, Kazemi A. Bar fracture modeling in progressive collapse analysis of reinforced concrete structures. Eng Struct 2011; 33(2): 401-409.

[16]  FarhangVesali N, Valipour H, Samali B, Foster S. Development of arching action in longitudinally-restrained reinforced concrete beams. Constr Build Mater 2013; 47: 7-19.

[17]  Alogla K, Weekes L, Augusthus-Nelson L. A new mitigation scheme to resist progressive collapse of RC structures. Constr Build Mater 2016; 125: 533-545.

[18]  Choi H, Kim J. Progressive collapse-resisting capacity of RC beam-column sub-assemblage. Mag Concr Res 2011; 63(4): 297-310.

[19]  Sadek F, Main JA, Lew HS, Bao Y. Testing and analysis of steel and concrete beam-column assemblies under a column removal scenario. J Struct Eng 2011; 137(9): 881-892.

[20]  Rankin GIB, Long AE. Arching action strength enhancement in laterally-restrained slab strips. Proceedings of the Institution of Civil Engineers-Structures and Buildings 1997; 122(4): 461-467.

[21]  Park R, Gamble WL. Reinforced concrete slabs. John Wiley & Sons 2000.

[22]  Yu J, Tan KH. Analytical model for the capacity of compressive arch action of reinforced concrete sub-assemblages. Mag Concr Res 2014; 66(3): 109-126.

[23]  Kang SB, Tan KH. Analytical study on reinforced concrete frames subject to compressive arch action. Eng Struct 2017; 141: 373-385.

[24]  American Concrete Institute (ACI). Building code requirements for structural concrete (ACI 318-14) and commentary (318R-14). Detroit, MI. 2014.

[25]  Niu JX, Su YP, Wang HX. Tentative studies on collapse resistance capacity of reinforced concrete frame beam. Proceeding of the 20th National Conference on Structural Engineering. Beijing: Engineering Mechanics Press 2011; 377-382 (in Chinese)

[26]  Chen MH, Song XS, Su YP. Influence of reinforcement ratio on ultimate bearing capacity of rein-forced concrete frame beams: test study on arch action. Journal of Natural Disasters 2010; 1: 44-48. (in Chinese)

[27]  Qian K, Li B. Slab effects on response of reinforced concrete substructures after loss of corner column. ACI Struct J 2012; 109(6): 845-855.

[28]  Prasad S, Hutchinson TC. Evaluation of older reinforced concrete floor slabs under corner support failure. ACI Struct J 2014; 111(4): 839-849.

[29]  Dat PX, Tan KH. Experimental study of beam–slab substructures subjected to a penultimate-internal column loss. Eng Struct 2013; 55: 2-15.

[30]  Mazzoni S, McKenna F, Scott MH, Fenves GL. The open system for earthquake engineering simulation (OpenSees). User command-language manual. Berkeley: Pacific Earthquake Engineering Research Center. University of California. 2006.

[31]  Ren PQ, Li Y, Guan H, Lu XZ. Progressive collapse resistance of two typical high-rise RC frame shear wall structures. J Perform Constr Facil 2015; 29(3): 04014087.

[32]  Lin KQ, Li, Y, Lu XZ, Guan H. Effects of seismic and progressive collapse designs on the vulnerability of RC frame structures. J Perform Constr Facil 2017; 31(1): 04016079.

[33]  Bao Y, Kunnath SK, El-Tawil S, Lew HS. Macromodel-based simulation of progressive collapse: RC frame structures. J Struct Eng 2008; 134(7): 1079-1091.

[34]  Talaat M, Mosalam KM. Modeling progressive collapse in reinforced concrete buildings using direct element removal. Earthq Eng Struct Dyn 2009; 38(5): 609-634.

[35]  Kazemi-Moghaddam A, Sasani M. Progressive collapse evaluation of Murrah Federal Building following sudden loss of column G20. Eng Struct 2015; 89: 162-171.

[36]  Pan WH, Tao MX, Nie JG. Fiber beam-column element model considering reinforcement anchorage slip in the footing. B Earthq Eng 2017; 15(3): 991-1018.

[37]  Yu J, Tan KH. Experimental and numerical investigation on progressive collapse resistance of reinforced concrete beam column sub-assemblages. Eng Struct 2013; 55: 90-106.

[38]  Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD). Code for design of concrete structures. GB50010-2010, Beijing, China. 2010. (in Chinese)

Appendix A

A set of 50 tests considering a mid-column removal scenario are collected from published literature, of which 45 are beam specimens [5-7, 10, 13-17, 25-26] and 5 are beam-slab specimens [7].

Table A.1. Summary of beam specimens [5-7, 10, 13-17, 25-26].

Note: ^*1 The boundary stiffness is used to calculate the boundary movement t, which is required in Equations 2-3 in the Park & Gamble’s model.

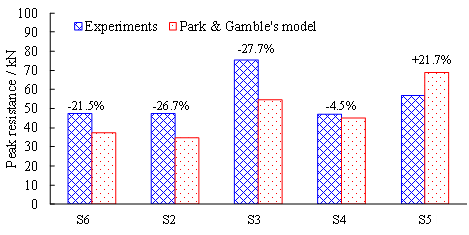
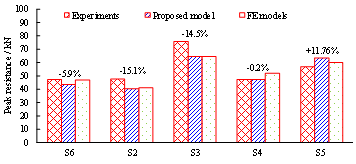
Table A.2. Summary of beam-slab specimens [7].

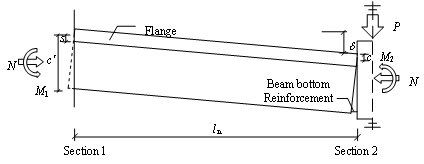
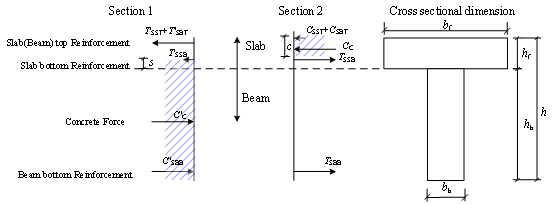
Note: ^*1 Definitions of h, b_b, h_f and b_f are given in Fig. 7 and Table 1.

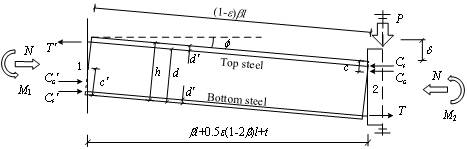
Appendix B

Detailed CAA resistance calculation procedure for the beam-slab specimen (Specimen S6 of Ren et al. [7]).