Proceedings of International Symposium on Bond Behaviour of FRP in Structures (BBFS 2005), Dec, 7-9, Hong Kong, China, pp 371-380 Chen and Teng (eds) © 2005 International Institute for FRP in Construction SIZE EFFECT of shear coNTRIBUTION OF externally BONDED FRP U-JACKETs for RC BEAMS Z. Qu1,2 , X. Z. Lu1,2, L. P. Ye1,2 1 Department of Civil Engineering, Tsinghua University, Beijing, China, 100084, China 2 Key Laboratory of Structural Engineering and Vibration of China Education Ministry, Email: qz@mails.tsinghua.edu.cn; luxinzheng@263.net; ylp@tsinghua.edu.cn Download PDF version ABSTRACT It is well known that size effect exists in the shear strength of RC beams. Larger beams have a smaller nominal maximum shear strength. The size effect in RC beams shear strengthened with FRP has not been considered in existing predictive models. In these strengthened beams, the size effect may exist in the shear contributions of both RC beams and FRP. To better understand the shear strengthening and its corresponding size effect, a series of geometrically similar concrete beams strengthened with CFRP U-jackets were designed and tested in this study. The total shear strength of a strengthened RC beam is considered to consist of three components which are the shear contribution of the RC beam, and the direct and indirect shear contributions of the FRP. The direct shear contribution of FRP is obtained in this study with careful experimental measurements. An improved predictive model is proposed, which can obviously remove the size effect on direct FRP shear contribution. More studies are needed to quantify the indirect FRP shear contribution. KEYWORDS FRP, RC beams, shear strength, experiment, size effect.

Introduction Extensive research has shown that size effect exists in the shear strength of RC beams without stirrups, which means that larger beams have smaller nominal shear strength. Fracture mechanics has been proved to be a powerful tool to solve the size effect problem. Bazant (1984) proposed a size effect theory considering stress redistribution and fracture energy release which was proved to be reasonable by an experimental study (Bazant 1991). Walraven and Lehwalter (1994) extended the application of Bazant¡¯s size effect theory to short beams with shear reinforcement and observed significant size effect on the shear strengths in their tests. The wide use of FRP strengthening in civil engineering during the last decade has brought new problems to size effect. A lot research has been devoted to the shear strength of FRP strengthened RC beams but few considered size effect. Most existing models for predicting the shear contribution of FRP sheets adopted a superposition method, which assumes that the shear strength of an FRP strengthened RC beam is the sum of two components: the RC contribution and the FRP contribution. The RC contribution is considered to be the same as the shear strength of the RC beam without strengthening, whilst the FRP contribution is estimated with a sectional method whose generalized equation is shown in Eq.1. (1) where Vf is the shear contribution of FRP sheets;            Af is the sectional area of FRP sheets within a distance of sf;            Ef is the Young¡¯s modulus of FRP sheets;            sf is the central spacing of FRP sheets;            q and b are the inclination angles of the diagonal crack and FRP sheets respectively, relative to the longitudinal axis of the beam;            hfe is the effective height of FRP sheets;            e fe is the effective strain of FRP sheets, which is the key parameter of this kind of model. Some of these models such as Chen and Teng (2003a, b) and Lu (2004) give satisfying predictions of FRP contributions with superposition method. However, indirect shear contribution of FRP such as the enhancement of aggregate interlock on the shear crack surface is not considered explicitly in Eq.1. The FRP shear contribution in Eq.1 is indeed a total shear force containing both direct and indirect shear contributions. As a result, models of this kind can hardly reveal the nature of this problem and size effect may also exist in the prediction of these models. Best fitting curves based on 35 beam tests (Lu, 2004) for the relationships between predicted FRP shear contributions and tests with different models are shown in Figure 1. The figure clearly shows that lower predictions appear in larger beams, which indicates a size effect on shear contribution of FRP sheets externally bonded to RC beams which is contrary to that of RC beams with or without shear reinforcement. Figure 1 Size effect on shear contribution of FRP sheets In this paper, the shear contribution of FRP sheets is examined in depth with the assistance of a test program. An improved finite element model is proposed to predict the direct shear contribution of FRP which shows good agreement with the test results in this study and little size effect. More studies are still needed for the indirect shear contribution of FRP.

TEST SPECIMENS AND PROCEDURE Three RC beams strengthened with FRP U-jackets, which were 3D geometrically similar, were tested. Three corresponding control beams without strengthening were also tested. In order to study the size effect in the shear strength, the span and thickness of the beam, as well as the width, space and thickness of FRP U-jackets, were increased proportionally with the height of the beams, so that all strengthened beams had the same FRP reinforced ratios rf . No steel stirrups were installed in the test span whilst sufficient stirrups were installed in the other span to avoid unexpected failure. All specimens had the same flexural reinforcement ratio. Some important parameters of the beams are listed in Figure 2 and Table 1. The flexural reinforcing bars were cold drawn deformed steel bars with yield strength of 400MPa. The ends of the flexural rebars in each beam were welded to each other with two layers of short steel bars to avoid anchorage failure. The nominal span-to-depth ratio l was 2.0 for all the beams. Here the shear span equals to the distance from loaded points to the centre of support. However, due to the relative large stiffness of backing strips at the loaded points and supported points, it was believed that the real shear span-to-depth ratio lr was 1.51, in which the shear span equals to the distance from the edge of loaded backing strip to the edge of supported backing strip. All the beams were cast in plywood mould from a single batch of concrete and were cured under the same condition for six days before the mould were stripped. The maximum aggregate size was about 30mm. The ages at which the beams were tested vary from 40 days to 90 days. The concrete strength of different beams, together with their shear strengths, are listed in Table 1. The thickness of CFRP strips is 0.111mm per-layer, with a Young¡¯s modulus Ef of 235GPa and tensile strength ff of 3550MPa. Figure 2 Configurations of specimens Table1 Basic design parameters and major test results of specimens Beam No. RC1 RC2 RC3 U4 U5 U6 Width b (mm) 100 200 300 100 200 300 Height h (mm) 200 400 600 200 400 600 Effective depth d (mm) 166 330 498 166 330 498 Shear Span a (mm) 340 680 1020 340 680 1020 Shear Span a0 (mm) 250 500 750 250 500 750 Steel reinforcement ratio r£¨%£© 4.1 4.5 4.2 4.1 4.5 4.2 Width of FRP strips wf (mm)       30 60 90 FRP effective thickness tf (mm)       0.111 0.222 0.333 Central spacing of FRP strips sf (mm)       50 100 150 Concrete compressive strength fcu (MPa) 51.2 49.7 50.5 51.2 51.2 51.0 Concrete tensile strength fts (MPa) 2.55 2.93 3.16 2.55 2.93 3.16 Concrete Young¡¯s Modulus Ec (MPa) 34272 Shear capacity of beam P (kN) 159.4 709.1* 1626.0 202.7 809.3 2017.9 * Specimen RC2 failed at the span with stirrups. TEST RESULTS AND DISCUSSIONS Components of the shear contribution of FRP sheets Generally the shear strength of FRP strengthened RC beam consists of two components which are shear contribution of RC beam VRC, and shear contribution of FRP Vf. Detailed research (Ye et al. 2002) has shown that the shear contribution of FRP Vf can be further divided into two portions, which are referred as the direct contribution Vfd and indirect contribution Vfi, respectively. The direct shear contribution Vfd is relatively easy to be understood which equals to the total tension of FRP strips. The indirect shear contribution Vfi represents all the other shear strength enhancements with FRP strengthening, such as the change of shear crack angle, enhanced aggregate interlock and reduction of damage concentration. As a result, the shear strength of an FRP strengthened RC beam can be presented as Eq. 2. (2a) (2b) where V is the shear strength of the FRP strengthened RC beam;            VRC is the shear contribution of the reinforced concrete beam;            Vf is the shear contribution of FRP sheets externally bonded on the web;            Vfd is the direct shear contribution of FRP, which equals the total FRP tensile force. Vfi is the indirect shear contribution of FRP, which represents the sum of all the other influences of FRP on the beam. Most existing models ignore Vfi for simplicity. However, Vfi may play an important role when estimating the overall shear contribution of FRP sheets. Figure 2 shows the development of FRP direct shear contribution ratio Vfd / V for the three specimens. Here Vfd equal the summation of FRP tensile forces calculated from the measured FRP strains. This ratio increases with the decrease of the beam height. The sum of FRP tensions suddenly drops when an FRP strip detaches from the concrete. The released forces from the detached FRP strip are transferred to other components of the beam, such as the steel reinforcement or the concrete. Since the total loading is still increasing without any sudden change, the sudden drop of FRP direct contribution means a sudden increase to the FRP indirect shear contribution Vfi. Another phenomenon in Figure 2 is that larger beams take a longer period from the first FRP strip separation to the ultimate state, which indicates that the larger the beam, the more important the Vfi is. Figure 2 Development of the direct shear contribution of FRP sheets

The direct shear contribution of FRP sheets Vfd Comparison between Vfd and the strength of direct-pull tests The major function of FRP sheets before failure is to provide tensions to resist the shear force. The loading condition of FRP U-jackets externally bonded on the beam is similar to that of FRP sheets in a direct-pull test as shown in Figure 3. The summation of these tensions is equal to Vfd, whose maximum value is generally reached just before the first FRP sheet fails due to debonding. The interaction between different FRP sheets is quite weak and it may be ignored before Vfd reaches its maximum value. The major difference between FRP externally bonded on the side in shear and FRP in a direct-pull test is the concrete stress state underneath the FRP sheets. (a) FRP externally bonded on the web in shear          (b) Direct-pull test Figure 3 Loading condition of FRP sheets In the direct-pull test, the concrete underneath the FRP is basically in a pure shear stress state. For FRP sheets bonded on the side of a beam, besides the FRP-to-concrete interfacial stresses, the concrete is part of the strut of the beam which carries a compressive stress approximately parallel to the diagonal crack and a tensile stress perpendicular to the compressive stress. So the stress state is much more complex and the strut stress may reduce the FRP-to-concrete interfacial strength, which results in a reduction of effective FRP debonding strain. Reduction of concrete tension strength ft Lu (2004) established his FRP shear contribution model by combining his bond-slip relationship and simplified diagonal crack models, in which the bond-slip relationship is obtained from direct-pull tests. According to the aforementioned comparison, the FRP-to-concrete interfacial strength needs to be reduced when such bond-slip relationship is applied to FRP-to-concrete interface in shear strengthening. The concrete tensile strength ft is critical for the FRP-to-concrete interfacial strength, since the debonding mode is due to the cracking of the concrete underneath the FRP sheets. Figure 4 Superposition of stress states of concrete in the strut underneath the FRP sheets Figure 4 demonstrates different stress states of concrete and their superposition. Experimental observation also finds that the FRP debonding failure and RC beam shear failure are very close to each other, though they do not happen at the same time. Thus, the two stress state components (State A and B in Figure 4) in the concrete strut underneath the FRP can be assumed to have reached their ultimate states when debonding failure happens. In the pure shear state (State A), the shear stress t f is assumed to be equal to the peak average bond stress t ave (Eq.3), (Lu et al. 2005b). The biaxial stress state (State B) when strut fails is debatable. Different researchers give different definitions. In this study, the compressive stress in the strut at failure is assumed to equal to 0.85fc¡¯ (Eq.4) (Alshegeir & Ramires 1990). The tensile strain of the strut at failure is assumed to be twice the concrete peak tensile strain e t,p, because some tiny but visible shear cracks are found in concrete underneath the FRP above the critical diagonal crack. If e t,p is calculated from Eq.5 (Guo 1997), the corresponding tensile stress of the strut can be found from Eq.6 (Belarbi & Hsu,1994). (3) (4) (5) (6) where fc¡¯ equals to 0.8fcu, wf is the width of the FRP sheets, sf is the central spacing of FRP sheets. In State B of Figure 4, q  is the average diagonal crack angle which equals 33º for the strengthened specimens in this study. A coordinate system transformation is needed to transform the biaxial stress of the strut sc and st to the global coordinate system sx, sy and t c, while t f in State A does not need any change. So the stress tensor in State C under global coordinate system can be given as Eq.7. (7) A reduced tensile strength of concrete ft¡¯ can be finally obtained for the triaixial stress state in Eq. 7 following the failure criterion proposed by the Chinese Academy of Building Research (2002) and Guo (2003): (8a) (8b) where ft¡¯ is reduced concrete tensile strength, which will be used in the following finite element analysis; s1 and s3 are the major and minor principal stress, respectively; ft and fc are the tensile and compressive strength of concrete, respectively. The reduced concrete tensile strengths of the three specimens are listed in Table 2, compared with their original tensile strengths. Table 2 Tensile strength of concrete (MPa)   U4 U5 U6 Reduced tensile strength ft¡¯ 2.12 2.25 2.34 Tensile strength ft 2.55 2.93 3.16

Finite element analysis The upper half of the critical FRP that may be separated from the beam was modelled with the truss-spring model as in Lu et al. (2005a) (Figure 5).  The FRP sheets are simulated using a series of truss elements for simplicity. Each node of the truss elements is connected to the concrete surface with a nonlinear spring element. A pre-defined slip field is applied at the end of the FRP sheets to simulate the opening of the diagonal crack. The properties of the spring were calculated based on the FRP-to-concrete interface bond-slip relationship proposed by Lu et al. (2005b) using the reduced concrete tensile strength ft¡¯ instead of ft. Three different simplified diagonal crack models are presented by Lu et al (2005a) as shown in Figure 6. For each diagonal crack model, there is a corresponding slip field. Each slip field is applied to the finite element model for the largest specimen U6. Figure 7 compares the FRP tensile strain distributions before debonding along the diagonal crack obtained from different slip fields. It can be seen that Crack model A gives the closest agreement with the test result due to sufficient flexural reinforcement which limits the cracking opening at the bottom of the beam. Crack model A will be adopted in the following calculations. 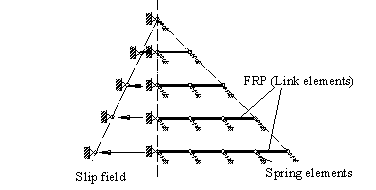Figure 5 Simplified FE model for externally bonded FRP U-jackets on RC beam (a) Model A                        (b) Model B                       (c) Model C Figure 6 Simplified diagonal crack models by Lu et al. 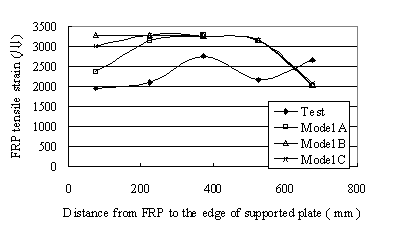(2005a) Figure 7 FRP strain distribution for different diagonal crack models: specimen U6 As aforementioned, the maximum value of Vfd is reached before the first FRP sheet completely debonds and Vfd is equal to the sum of tensions provided by FRP sheets along the diagonal crack. As an elastic material, the tension in FRP is equal to the product of the tensile strain and the Young¡¯s modulus of FRP. So the distribution of FRP tensile strain along the diagonal crack is directly related to Vfd. The average tensile strain of FRP sheets when Vfd reaches its maximum value is called FRP average peak strain. Finite element analyses were carried out for all the three specimens and Figure 8 compares the calculated distributions of FRP tensile strain before the first FRP sheets fails along the diagonal cracks with the test results. The simulation gives satisfying results. 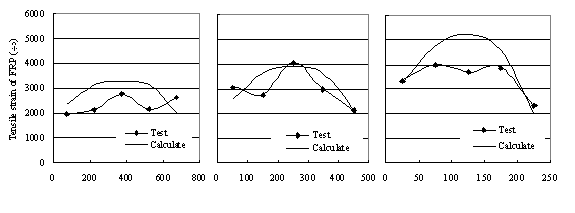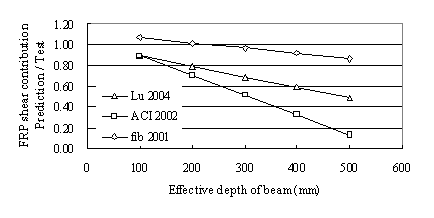Distance from FRP to support plate (mm)              (a) U6  h=600mm                             (b) U5  h=400mm                                (c) U4  h=200mm Figure 8 Measured FRP strain distribution along the diagonal crack versus FE prediction Figure 9 compares the FRP peak average strains of different specimens obtained by tests and some existing models. The finite element model adopted in this study is the same as the one used in Lu et al. (2005a) except that the reduced concrete tensile strength was used here. Lu et al¡¯s model (2005a) obviously overestimates the direct contribution of FRP from Figure 9. The results of all other models are also much larger than that of the present finite element analysis, mainly because all these models take the indirect shear contribution of FRP sheets Vfi as part of direct portion Vfd. It should be mentioned that in this test program, the tension-compression strength ratio of the concrete is much lower than most empirical formulas. For example, U4 has a cubic strength of 51.2MPa but a tensile strength of 2.55MPa. This tensile strength is smaller than the value calculated from the empirical formulas proposed by the Chinese code in which ft can be found from fcu to be 3.44MPa. As a result, Chen and Teng¡¯s model (2003b) which is based on the compressive strength of concrete for convenience of practical design gives worse prediction than Lu et al¡¯s model (2005a) which is based on the tensile strength of concrete. It also implies that the interfacial debonding is mainly governed by the tensile strength of concrete underneath FRP, which was discussed in detail in Lu et al. (2005b). The peak FRP average strain decreases as the height of beam increases for the test specimens. Note that the thickness of FRP is proportional to the beam height. The FE predictions give a satisfying prediction of this trend. Most existing models such as Lu et al (2005a), Chen & Teng (2003b), ACI 440 (2002) also demonstrated similar trends despite over estimating the peak strains. Since the descending trend of FRP peak average strain can be predicted with satisfactory accuracy, little size effect exists on the direct shear contribution of FRP sheets Vfd especially when it is predicted with the reduced ft as proposed in this study. So the size effect on the FRP shear contribution mainly comes from the indirect shear contribution Vfi. 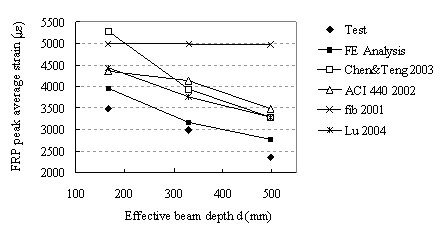Figure 9 The peak average strains of FRP sheets The indirect shear contribution of FRP sheets Vfi Apart from tension forces which directly resist the shear force, the FRP sheets have many other effects on the mechanical behaviour of the reinforced concrete beam. These effects are considered as the indirect shear contribution Vfi, which is very complicated and can hardly be obtained directly from tests. However, some concepts are discussed as follows. Firstly, the inclination angle of diagonal crack decreases after the beam being strengthened by FRP U-jackets as shown in Figure 10. This results in a larger uncracked concrete region near the loaded point which enhances the loading capacity of the uncracked concrete and flexural compression zone. 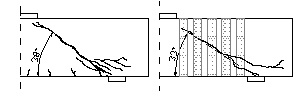(a) RC1                              (b) U4 Figure 10 Diagonal cracks in RC1 and U4 at failure Secondly, the FRP sheets externally bonded on the side resist the opening of the diagonal crack, which in turn enhance the crack-surface shear retention and increase the residual tensile stresses across the cracks. Figure 11 shows the distribution of the principal tensile strain in RC3 and U6 obtained from photogrammetry. The larger the tensile strain, the darker it is on the figure. An obvious diagonally cracked region is seen in RC3 (Figure 11a) while the tensile strain in the diagonal cracked region in U6 is relatively small (Figure 11b), indicating a smaller crack width. (a) RC3                              (b) U6 Figure 11 Principle tensile strain distributions on the webs of RC3 and U6  at a load of P» 0.75/Pu Also, the dowel action plays a more important role in FRP strengthened RC beam since the concrete supporting the flexure steel bars is enhanced by FRP sheets and it is believed that most of the forces released by FRP failure are carried by dowel action. As the components are similar, the indirect shear contribution Vfi may be simulated by the shear strength of an equivalent RC beam without web reinforcement, i.e. the size effect on Vfi may be converted to the size effect on RC beam without web reinforcement. CONCLUSIONS 1.        The shear strength of FRP strengthened RC beams may be divided into three components, the shear contribution of RC beams, the direct shear contribution of FRP sheets and the indirect contribution of FRP sheets. 2.        The direct shear contribution of FRP sheets is equivalent to the load capacity of a direct-pull test, where the concrete tensile strength ft has to be reduced to consider the different stress states of the concrete underneath the FRP. 3.        The direct shear contribution of FRP sheets shows little size effect. ACKNOWLEDGMENTS The authors would like to thank Dr J.F. Chen and Professor J.M. Rotter of Edinburgh University, UK for their contributions in the experimental design, discussions and writing of the paper. They would also like to acknowledge the financial supports provided by the Natural Science Foundation of China (National Key Project No. 50238030), the Royal Society through Royal Society-NSFC China-UK Joint Project (Grant No. IS 16657) and the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No: PolyU 5151/03E). References ACI 440 (2002). ACI 440.2R-02 Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. Alshegeir, A. and Ramires, J. A. (1990). ¡°Analysis of disturbed regions with strut-and-tie models¡±. Structure Engineering Rep. No. CE-STR-90-1, Purdue University, West Lafayette, India. Belarbi, A. and Hsu, T. T. C. (1994). ¡°Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete¡±, ACI Structual Journal, 91(4), 465-474 Chen, J. F. and Teng, J. G. (2003a). ¡°Shear capacity of FRP-strengthened RC beams: FRP debonding¡±, Construction and Building Maerials, 129(5), 615-625. Chen, J.F. and Teng, J.G. (2003b). ¡°Shear capacity of FRP strengthened RC beams: fibre reinforced polymer rupture¡±, Journal of Structural Engineering, ASCE, 129(5), 615-625. China Academy of Building Research, (2002). ¡°Code for design of concrete structures¡±. China Architecture and Building Press, Beijing, China, 93-98 fib (2001). ¡°Externally bonded FRP reinforcement for RC structures¡±.  Guo, Z. H. (1997). ¡°The strength and deformation of concrete (Experimental foundation and constitutive law)¡±, Tsinghua Univ. Press, Beijing, China. Guo, Z. H., Shi, X. D.,(2003). ¡°Priciples and analysis of reinforced concrete¡±. Tsinghua Univ. Press, Beijing, China, 24-32 Lu, X. Z. (2004). ¡°Studies on FRP-concrete interface¡±. PhD Thesis, Tsinghua University, Beijing, China. Lu, X. Z., Chen J. F., Ye L. P., Teng J. G., Rotter J. M., (2005a). ¡°Theoretical analysis of FRP stress distribution in U jacketed RC beams¡±, Proc. 3rd Int. Conference on Composites in Construction (CCC2005), Lyon, France, July, 2005, 541-548. Lu X. Z., Teng JG., Ye L.P., Jiang J.J., (2005b). ¡°Bond-slip models for FRP sheets/plates externally bonded to concrete¡±. Engineering Structures. 27(6), 938-950. . Ye L. P., Yue Q. R., Zhao S. H., Li Q. W., ( 2002). ¡°Shear strength of reinforced concrete columns strengthened with carbon-fiber-reinforced plastic sheet¡±, Journal of Structural Engineering, ASCE., 128 (12), 1527-1534.

Introduction

Research

Application

Teaching

Publications

Download

Issues

Others