A Hysteretic Model of Conventional Steel Braces and an Analysis of the Collapse Prevention Effect of Brace Strengthening

Shengnan Huang ^1,a, Xinzheng Lu ^2,b, Lieping Ye ^2,c

¹ Civil and Environmental Engineering Institute, University of Science & Technology Beijing, Beijing, China, 100083

² Department of Civil Engineering, Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry, Tsinghua University, Beijing, China, 100084

^a huangcn03@mails.tsinghua.edu.cn, ^b luxz@tsinghua.edu.cn, ^c ylp@tsinghua.edu.cn

Applied Mechanics and Materials, 2012, 174-177: 3-10.

Keywords: brace; hysteretic model, Wenchuan Earthquake; collapse probability; strengthening.

Abstract. A hysteretic model of conventional steel braces consisting of 18 parameters is proposed. This model is able to simulate the hysteretic behavior of conventional steel braces accurately. The collapse-prevention strengthening effect with steel braces for a typical reinforced concrete (RC) frame that was close to the epicenter and collapsed during the Great Wenchuan Earthquake is discussed via push-over analysis and collapse fragility analysis based on incremental dynamic analysis. The result could be referred to for the seismic collapse prevention design of RC frames.

DOI: 10.4028/www.scientific.net/AMM.174-177.3

If you need the PDF version of this paper, please email to luxinzheng@sina.com

Introduction

During the Great Wenchuan Earthquake, there were many places where the actual intensity was much higher than the fortification level. Not only numerous old buildings but also some structures that were designed in accordance with the latest seismic design code collapsed ^[1,2]. For example, the new classroom buildings of Xuankou Middle School, which were close to the epicenter and were designed following the 2001 version of the Code for Seismic Design of Buildings ^[1], were seriously damaged (Figure 1), and portions of the buildings collapsed in the aftershock ^[3]. Hence, more attention has been paid by the civil engineers to the earthquake-induced collapse resistance of buildings after the Wenchuan Earthquake.

Fig. 1 Seismic damage of buildings in Xuankou Middle School (From Xinhua News Agency)

After the Wenchuan Earthquake, to improve the seismic resistance of existing buildings, structural seismic strengthening work was carried out throughout China, especially in school buildings. Among many different strengthening methods, installing steel braces is a common and convenient method. However, little work has been performed to quantitatively evaluate the earthquake-induced collapse resistance of the strengthened structures. In recent years, collapse fragility analysis based on incremental dynamic analysis (IDA) has provided relatively quantitative criteria to evaluate the collapse resistance of different structural systems ^[4]. When using IDA, a group of representative earthquake ground motions containing more than 20 records are selected. The ground motions are input to the structures one by one to implement the dynamic time-history analysis. The ground-motion intensity is increased systematically until the structure collapses, and the vulnerability of the structure against earthquake can be obtained. By comparing the vulnerabilities of different structural systems, the seismic resistance can be quantitatively evaluated. In this paper, a typical reinforced concrete (RC) frame classroom building, shown in Figure 1, is selected as the benchmark case to discuss the collapse resistance of the strengthened structures via IDA.

The hysteretic model of conventional steel brace

For RC frame structures strengthened with steel braces, the structural lateral-resistance and the lateral-stiffness are enhanced and the energy dissipation capacity is improved due to the plastic deformation of the brace, which improves the collapse resistance when subjected to a strong earthquake. Because the structural plastic deformation is mainly concentrated inside the braces, the hysteresis characteristic of steel braces is very important to the structural seismic performance, especially to the structural collapse resistance. Hence, a numerical model that is able to accurately simulate the hysteretic behavior of steel braces is needed. The existing hysteretic brace model cannot precisely represent all of the nonlinear features, including the yielding, hardening, softening, pinching, cumulative damage, unloading stiffness degradation, and compressive instability. Therefore, a reasonable hysteretic brace model is needed to study the collapse resistance of strengthened structures.

The features of the steel brace hysteretic model include the yielding, hardening and softening behaviors when the brace is in tension, and the yielding and stiffness/strength deterioration when the brace is in compression. These complicated behaviors are significant challenges for the simulation. Generally, there are three methods to model the hysteretic performance of steel brace, including the finite element approach, the plastic hinge approach, and the phenomenological description approach.

The finite element approach divides the brace into many discrete beam elements ^[5] or shell elements ^[6] to represent the geometric properties and material properties of the brace. Initial geometric imperfections are defined in the middle of the brace to simulate the hysteretic buckling behavior. This method is very adaptive and precise. The model parameters, which only describe the geometric properties and material properties, are easy to determine. However, the computational cost is very high. Therefore, this method is mostly used to study the hysteretic performance of a single steel brace. It is difficult to apply to the seismic simulation of an entire structure.

The plastic hinge approach divides the single brace into two elastic beam elements with a plastic hinge in the middle of the brace (i.e., the joint of the two elastic beam elements) ^[7,8]. The hysteretic behavior of the brace is simulated by the nonlinear flexural behavior of the plastic hinge. It is assumed that the deformation is concentrated inside the plastic hinge, and the plastic properties that change along the longitudinal direction are not considered. Therefore, the simulation accuracy of this method is lower than that of the finite element approach. ^[7-10].

The phenomenological description approach directly models the deformation properties and the hysteretic behavior of the brace in accordance with the experimental observation^[11-13]. The controlling parameters are determined based on the experimental results. If the hysteretic rule is reasonable, the hysteretic behavior will be well described.

In this paper, on the basis of the plastic hinge hysteretic model with 10 parameters that was developed by Lu et al. ^[14], a hysteretic brace model that consists of 18 parameters is proposed, and this model can comprehensively simulate the complex hysteretic behavior of conventional steel braces, as shown in Figure 2. In this model, many features can be considered, such as the yielding, hardening and softening properties, the pinching properties, the cumulated damage properties of the brace under cycle loading, the different yielding strength between tension and compression, the deterioration properties of unloading stiffness, the deterioration properties of stiffness and strength caused by the instability of braces under compression.

Fig. 2 Hysteresis model of steel braces with 18 parameters

In this model, 18 parameters need to be defined, as shown in Table 1. By adjusting the values of these parameters, many different hysteresis features can be simulated. The brace experiment conducted by Goggins et al. ^[15] is used as an example. A comparison between the calculated results and the experimental results of hysteresis curves is shown in Figure 3; the prediction agrees well with the test results.

Tab. 1 Parameter list of the brace model

Fig. 3 Comparison between the proposed model and the experimental result

Strengthening effect analysis

A typical RC frame classroom building (Figure 1), which is close to the Wenchuan Earthquake epicenter, is used as an example to analyze the strengthening effect of the steel brace. The plan for the classroom building is shown in Figure 4. The detailed phenomenon of seismic damage and the detailed structural information are described by Lu et al. ^[16]. A steel brace is assumed to be installed in the short axis direction of the frame, along which the frame collapsed. 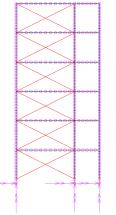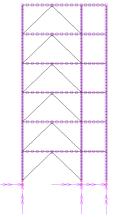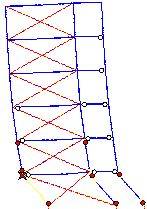Two schemes (i.e., X-shaped and A-shaped) for the steel brace installation are compared, as shown in Figure 5. To study the influence of the cross-section and numbers of the braces on the structural collapse resistance, five load cases are compared as follows:

(1)   Load Case 1: The section of the steel brace is I25A, install a suit of braces every 2 frames (Load case No: I25).

(2)   Load Case 2: The section of the steel brace is I20A, install a suit of braces every 2 frames (Load case No: I20).

(3)   Load Case 3: The section of the steel brace is I20A, install a suit of braces every 4 frames (Load case No: I20-1/2).

(4)   Load Case 4: The section of the steel brace is I20A, install a suit of braces every 8 frames (Load case No: I20-1/4).

(5)   Load Case 5: The section of the steel brace is I20A, install a suit of braces every 12 frames (Load case No: I20-1/6).

For Load Case 5, because the number of classrooms is limited, it is actually impossible to install a suit of braces every 6 classroom. Hence, this case was only studied theoretically.

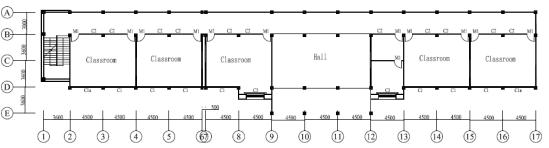
Fig. 4 Plan of the Classroom Building

The earthquake ground motions, which are used as the input of IDA, are 22 far-field ground motions suggested by FEMA P695 ^[17]. Moreover, the widely used El-Centro ground motion is also used as the input of the IDA. The structures are modeled with the THUFIBER Program ^[14], and the influences of the foundations and floor slabs are considered. The details of the model are described by Lu et al. ^[16]. To allow for the influence of the steel stirrups, the confined concrete constitutive law that is proposed by Bousalem and Chikh ^[18] is used to model the core concrete. Because of the excellent nonlinear computing ability of the THUFIBER program, the following collapse criterion is used: the structure is deformed so much that the structure is unable to safely provide enough free space ^[14].

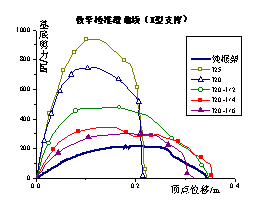
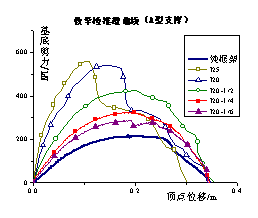
Push-over results The push-over results of different load cases are shown in Figure 6. As the number of braces increases, the stiffness and bearing capacity are improved. This result is the positive effect of the brace strengthening ^[3]. However, the ductility of the frame decreases with an increase in the brace number because the brace will bring additional axial force to the column. Because the axial force ratio of the columns has approached to the ultimate value ^[16], the additional axial force will result in a decrease in the ductility of the frame. This is the negative effect of the brace strengthening on the seismic resistance. Because both positive effect and negative effects are observed in the push-over analysis, it is difficult to draw a conclusion about the brace strengthening effect from the push-over results. Hence, collapsed fragility analyses based on IDA for different load cases are analyzed as follows to compare the effects of different strengthening schemes.

Fig.6 Push-over result of steel brace strengthening scheme

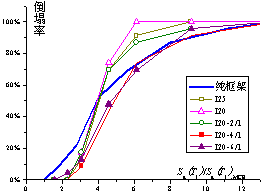
Collapsed fragility analysis results The collapsed fragility analysis results of the steel brace strengthening scheme are shown in Figure 7. In Figure 7, the vertical axis is the collapsed possibility, which is the proportion of collapsed ground motion records and total ground motion records at a given seismic intensity. The horizontal axis is the seismic intensity, and the spectral acceleration at structural fundamental period S_a(T₁) is used as the intensity measure. According to the work in Ref [3], [14] and [17], S_a(T₁) can reduce the dispersion of the IDA results. It can be observed from Figure 7 that after steel brace strengthening, the collapse possibility is reduced obviously under the maximal considered earthquake (S_a(T₁)=S_a(T₁)_,MCE). When S_a(T₁)=2S_a(T₁)_,MCE, the strengthening effect is also obvious. However, when S_a(T₁) is larger than 4 times S_a(T₁)_,MCE (S_a(T₁)>4S_a(T₁)_,MCE), the collapse possibility unexpectedly increases. The reasons for this increase are as follows.

Fig.7 Collapse possibility curves of conventional brace strengthening scheme

For RC frame structures strengthened with braces, the braces have two effects on the seismic resistance of the structure. On one hand, the structural bearing capacity is enhanced, and the energy dissipation capacity is improved due to the plastic deformation of the brace. Therefore, the structural collapses resistance is improved. On the other hand, the structural stiffness is enhanced, so the seismic load is increased. Furthermore, the axial forces of columns are increased due to the axial load of the brace. Therefore, the deformation capacities of columns are reduced, which will weaken the structural collapse resistance.

In general, if the energy input of ground motion is relatively stable or the ground motion intensity is small, the energy dissipation capacity of the braces will be fully used. Hence, the structural collapse resistance will be improved. However, if the earthquake is pulse-type or the ground motion intensity is large, the structure will collapse very quickly, and the energy dissipation capacity of the braces will not be fully used. In this situation, the negative effect due to the increasing axial force in the column will be a dominant factor.

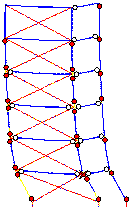
Typical failure modes of the steel brace¨Cstrengthened structures are shown in Figure 8. Figure 8a shows the failure mode in which the collapse resistance is improved after strengthening; the input ground motion record is from Kobe, Japan, 1995. Without strengthening, the structure will collapse when S_a is larger than 2.5 m/s. After strengthening, the structure will collapse when S_a is larger than 4.9 m/s. Subjected to this ground motion, the structure has experienced a few of cycles of vibration before it collapses, and the energy dissipation capacity of the braces has been fully used. The structural plastic hinges are uniformly distributed, which also provides a better energy dissipation capacity. In Figure 8b, the input ground motion record is from Duzce, Turkey, 1999. Without strengthening, the structure will collapse when S_a is larger than 7.35 m/s. After strengthening, the structure will collapse when S_a is larger than 4.9 m/s. Hence, the structural collapse resistance is reduced because the Duzce record is a pulse-type earthquake. After the first pulse, the top of the side column in the bottom story has been destroyed because the deformation is too large. The energy dissipation capacity of the braces cannot be fully utilized. Moreover, the number of plastic hinges inside the building is also very limited. The energy dissipation capacity of the structure is not fully developed.

The collapse possibilities of different steel brace strengthening schemes are shown in Table 2. In Table 2, the collapse margin ratio (CMR) is defined as:

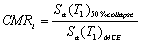                                                                                                                    (1)

where S_a(T₁)_50%collapse is the intensity of the input motions under which 50% of the ground motions will cause structural collapse. S_a(T₁)_MCE is the maximal considered earthquake intensity. The larger CMR is, the better the structural collapse resistance is. The CMR does not change monotonically with the brace number. Therefore, there is an optimal number for the brace strengthening scheme. Among these cases, Load Case 4 is the best choice.

Tab. 2 Collapse possibility of the conventional brace-strengthening scheme

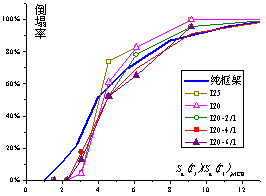
To compare the influence of different brace arrangements, the I20 Load Case is used as an example, and the comparison of the collapse possibilities is shown in Figure 9. With the same number and section of braces, the strengthening effect of the A-shaped brace is better than that of the X-shaped brace. This result is obtained because the X-shaped braces will bring more axial force to the bottom columns, which is unfavorable for structural collapse resistance.

Original frame

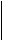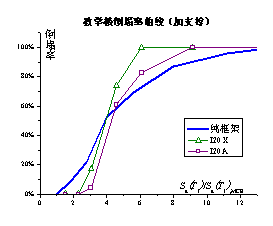
Fig. 9 Comparison of the collapse possibility curves of steel brace strengthening schemes

Conclusion

In this paper, a hysteretic model with 18 parameters is proposed. A typical RC frame classroom building, which is close to the Wenchuan Earthquake epicenter, is used as an example. Push-over analysis and IDA collapse fragility analysis are implemented, and the strengthening effects of the braces are discussed. The conclusions are as follows.

(1)In the proposed model with 18 parameters, many properties of the brace are considered, such as yielding, hardening and softening. The analysis results agree well with the experimental results, and the calculation process is simple.

(2)Bracing has some positive effects, such as dissipating energy and increasing the lateral load resistance. It also has some disadvantages, such as increasing the stiffness of the structure and the axial force of the columns. The structural collapse possibility is reduced under the maximal considered earthquake and mega-earthquake. However, the structural collapse possibility is unexpectedly increased under a much larger earthquake. Therefore, it is necessary to select a suitable strengthening scheme according to the actual project situation. The IDA method provides an analytical tool for studying the collapse resistance of brace-strengthened structures.

(3)For RC frame structures, the A-shaped brace scheme is better than the X-shaped scheme. This is because the brace forces in the bottom story do not directly transfer to the columns in the bottom story, which are the weakest portion of the building, so the negative effects are smaller.

References

[1]   Code for seismic design of buildings [S]. GB 50011-2001, Beijing: China Architecture and Building Press, 2001.(in Chinese)

[2]   Analysis on Building Seismic Damage in Wenchuan Earthquake, Journal of Building Structures [J], 2008, 29(4): 1-9. (in Chinese)

[3]   Ye LP, Lu XZ, Li Y, Design objectives and collapse prevention for building structures in mega-earthquake, Earthquake Engineering and Engineering Vibration, 2010, 9(2): 189-200.

[4]   Tang BX, Lu XZ, Ye LP, Shi W, Evaluation of collapse resistance of RC frame structures for Chinese schools in seismic design categories B and C, Earthquake Engineering and Engineering Vibration, 2011, 10(3): 369-377.

[5]   Lian WA, Zhang YC, Hysteretic behavior simulation and fatigue life prediction for the steel brace[J], Steel Structures, 2002, Sup. , 350-355. (in Chinese)

[6]   Shen L, Hysteretic behavior and design criterion of steel braces in high-rise building under cycle loading [D], Shanxi: Xi¡¯an University of Architecture and Technology, 2001. (in Chinese)

[7]   Alexander M. Remennkov, Warren R. Walpole. Modeling the inelastic cyclic behaviour of a bracing member for work-hardening material [J]. International Journal of Solids and Structures, 1997, 34(27): 3491-3515.

[8]   Ali Davaran, Narges Easazadeh Far. An inelastic model for low cycle fatigue prediction in steel braces [J]. Journal of Constructional Steel Research, 2009, 65(3): 523-530.

[9]   Murat Dicleli, Ertugrul Emre Calik. Physical Theory hysteretic model for steel braces [J]. Journal of Structural Engineering, 2007, 134(7): 1215-1228.

[10] Jun Jin, Sherif El-Tawil. Inelastic cyclic model for steel braces [J]. Journal of Engineering Mechanics, 2003, 129(5): 548-557.

[11] Nariman M. Haroun, Robin Shepherd. Inelastic behavior of X-bracing in plane frames [J]. Journal of Structural Engineering, 1986, 112(4): 764-780.

[12] K. Ikeda, S. A. Mahin. Cyclic response of steel braces [J]. Journal of Structural Engineering, 1986, 112(2): 342-361.

[13] Li GQ, Xie WB, Shen ZY, Simplified analytical model for the elasto-plastic analysis of high-rise braced steel frame [J], Building Structures, 1996, (11): 3-6. (in Chinese)

[14] Lu XZ. Ye LP, Miao ZW. Elasto-plastic analysis of buildings against earthquake [M], Beijing: China Architecture and Building Press, 2009. (in Chinese)

[15] J. M. Goggins, B. M. Broderick, A. Y. Elghazouli, A. S. Lucas. Experimental cyclic response of cold-formed hollow steel bracing members [J]. Engineering Structures, 2005, 27: 977-989.

[16] Lu XZ, Ye LP, Ma YH, Tang DY, Lessons from the collapse of typical RC frames in Xuankou School during the great Wenchuan Earthquake, Advances in Structural Engineering, 2012, 15(1): 139-153.

[17] Quantification of building seismic performance factors [S], ATC-63 Project Report (90% Draft), FEMA P695 / April 2008.

[18] B. Bousalem, N. Chikh. Development of a confined model for rectangular ordinary reinforced concrete columns [J]. Materials and Structures, 2007, 40: 605¨C613.