|
3 Computational models and seismic damage simulation
In order to understand the seismic damage
mentioned above, nonlinear finite element (FE) analysis was implemented to
simulate the seismic damage of Classroom Building A and Office Building H.
An accurate computational model that can
represent the actual mechanical properties of the structures is critical for
revealing the seismic damage mechanism. For structural elements in RC frames
whose strengths and ductility are strongly controlled by the axial force-bending
moment interaction, the fibre-beam-element model is widely accepted as suitable
for proper simulation (Lai et al. 1984; Spacone et al. 1996;
Taucer et al. 1991; Ye et al. 2006). However, fibre-beam-element
models are ˇămacro-scaleˇ± models (also referred to as ˇădiscrete finite element
(member) modelsˇ± by Spacone et al. (1996)), which have some difficulties
in simulating ˇămicro-scaleˇ± failures such as the failures inside footings
and joints. In addition, a trial simulation using the fibre-beam-element model,
which is in accordance with the conventional design computational model in
China, results in significantly different damage characteristics to those
of the actual seismic damage (to be introduced in detail in Section 3.1.4).
Therefore, a micro-macro-scale hybrid model
was proposed to provide a better approach to the simulation of seismic damage.
The macro-scale fibre-beam-element model was then improved to simulate the
actual behaviour of the structures based on the results of the micro-macro-scale
hybrid model. Finally, a large number of statistical analyses (incremental
dynamic analysis (IDA) (Vamvatsikos & Cornell, 2002) based on 23
ground motions) were undertaken with the improved fibre-beam-element model.
Collapse fragility curves were calculated to explain the differences in collapse
resistance between the office building and the classroom buildings and to
propose a corresponding optimized design.
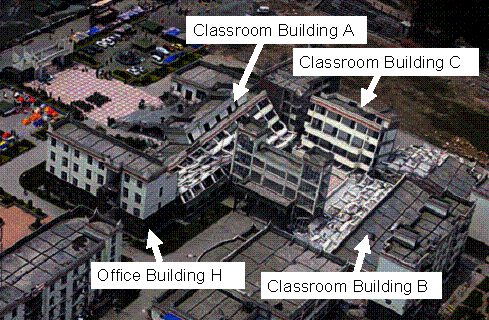
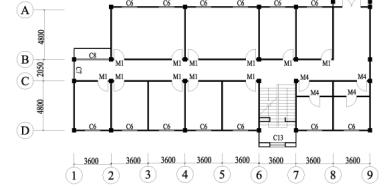
According to the on-site investigation, every
classroom building collapsed along its short axis (Figures 3 and 4). Therefore,
to simplify the simulation and highlight the most important factors, two-dimensional
nonlinear FE models were created for Classroom Building A on its short axis
(i.e., the actual collapse direction). For convenience, a two-dimensional
nonlinear FE model was also created for Office Building H on its short axis
to compare with Classroom Building A.
Several computational models were used in
the following discussion of seismic damage simulation. To avoid confusion,
these models are briefly summarized in Table 1. Further details are described
in sections below.
3.1 Fibre-beam-element model
The fibre-beam-element model has been widely
used to model RC frames whose failures are controlled by flexural behaviours
(Lai et al. 1984; Spacone et al. 1996; Taucer et al.
1991; Ye et al. 2006). In the fibre-beam-element model, the frame elements
(beams and columns) are modelled with beam elements, and the sections of the
beam elements are divided into individual fibres. Each fibre follows a uniaxial
constitutive law, and different fibres in the same section follow the assumption
that ˇăplane section remains planeˇ±. The fibre-beam-element model can simulate
the axial-flexural coupling of RC frames, and is easily adapted to different
section shapes.
3.1.1 Constitutive law of concrete
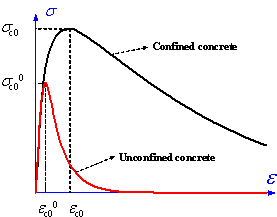
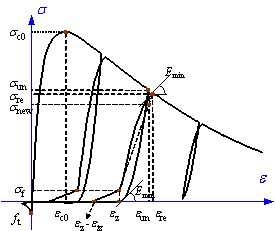
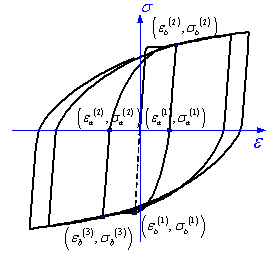
The stress-strain model proposed by L¨¦geron
& Paultre (2005) was used in this work to model the backbone curve of
concrete, a model which can represent the confinement of concrete due to stirrups
(Figure 8a). Parabolic curves proposed by Mander et al. (1998) were
adopted to model the concrete unloading and reloading paths. This model can
take account of the degradation of concrete strength and stiffness due to
cyclic loading (Figure 8b). An exponential model proposed by Jiang et al.
(2005) was used to model the softening branch of cracked concrete, a model
which also allows the ˇătension-stiffening effectˇ± of reinforced concrete can
be taken into account (Figure 8b).
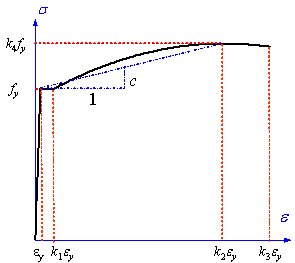
3.1.2
Constitutive law of steel
The stress-strain model proposed by Esmaeily
& Xiao (2005) was adopted to model the backbone curve of steel (Figure
9a). The model proposed by L¨¦geron et al. (2005) was adopted to model
the unloading and reloading paths, and also the Bauschinger effect of steel
(Figure 9b).
3.1.3 THUFIBER program
Based on the above material models, a fibre-beam-element
based program referred to as THUFIBER (Ye et al. 2006; Lu et al.
2008a,b; Miao et al. 2007) was developed by the authors, which can
be embedded into the general purpose FE software MSC.MARC using the user subroutine
UBEAM (MSC, 2005). Examples and benchmarks (Ye et al. 2006; Lu et
al. 2008a,b; Miao et al. 2007) show that this program can precisely
simulate the nonlinear behaviours of RC frames.
3.1.4 Problems in conventional design computational models
According to the conventional design computational
models for RC frames in China, the column feet in the bottom storey are fixed
to the foundation (i.e., no rotation of the footings), and only frame beams
and columns are included in the computational model. The contribution of the
floor slabs to the strength of the beams is not considered. The reinforcement
of the RC frame is designed to resist internal forces obtained from this computational
model. To ensure that the ˇăstrong column-weak beamˇ± failure mode occurs, the
Chinese Seismic Design Code (GB, 2001) requires:
SMc>hc SMb
(1)
where SMc is the total design bending moment in the
columns connected to a joint, SMb is the total design bending moment in the beams connected
to the same joint, and hc is a moment amplification factor. For RC
frames in Xuankou School, hc =1.1 (GB, 2001).
A fibre-beam-element model (referred as Macro-model
A in Table 1) was built in accordance with the above conventional design computational
model (i.e. floor slabs not considered and columns fixed to the foundation).
According to the orientation of Classroom Building A, the north-south (NS)
and the vertical (UD) components of the Shifang-Bajiao ground motion record,
which were obtained near the epicentre during the Great Wenchuan Earthquake,
were used as input to Macro-model A. The peak ground acceleration of the ground
motion was scaled to 1.0g to match the actual intensity at Xuankou School.
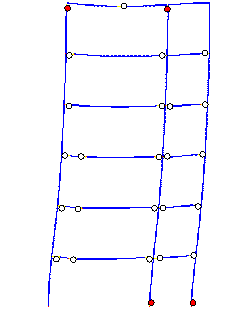
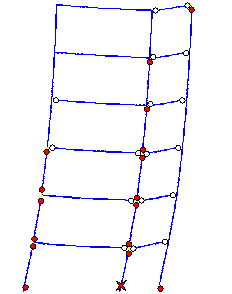
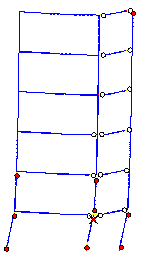
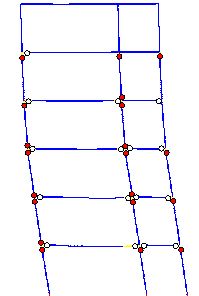
The failure mode predicted by Macro-model
A subjected to the Wenchuan NS+UD ground motions is shown in Figure 10, and
clearly differs from the actual failure mode in the following respects: (1)
most plastic hinges occur in the beams rather than in columns; (2) the damage
at the feet of columns in the bottom storey is more severe than at the top
of the columns. The collapse starts from a compression-bending failure at
the foot of the middle-column in the bottom storey.
Thus, Macro-model A is not consistent with
the actual behaviour of the structure. Further discussions were therefore
needed concerning the computational models appropriate for these structures.
3.1.5 Fibre-beam-element model allowing for the influence of slabs
Most of the plastic hinges predicted by Macro-model
A are located in the beams, which is significantly different from the actual
seismic damage. Through a preliminary analysis, the possible reason for this
difference is that Macro-model A, as well as Eqn. (1) in the Chinese Seismic
Design Code (GB, 2001), do not consider the strengthening effect of the floor
slabs on the frame beams. Actually, cast-in-situ RC slabs can work together
with the beams, significantly increasing the stiffness and strength of the
beams. Thus, a ˇăstrong beams-weak columnsˇ± failure mode may appear in cast-in-situ
RC frames such as Classroom Building A.
Therefore, to take into account the influence
of slabs, Macro-model A was improved. The frame beams were modelled as T-shaped
beams in the fibre-beam-element model. The flange of the T-beam represents
the floor slab. The thickness of the flange is equal to the thickness of the
slab, and the width of the flange on each side (i.e., the width of the slab
considered in the computation) is 6 times the thickness of the slab (ACI 2005,
Leon 1984). The flange has the same reinforcement as the slab. This macro-scale
fibre-beam-element model, which considers the slabs, is referred to as Macro-model
B in Table 1. The NS+UD components of the Wenchuan Earthquake ground motion
mentioned in Section 3.1.4 were now used as input to Macro-model B and the
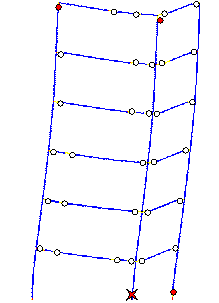
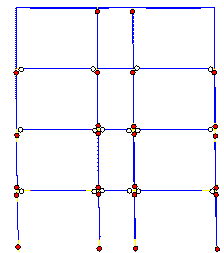
predicted failure mode is shown in Figure 11.
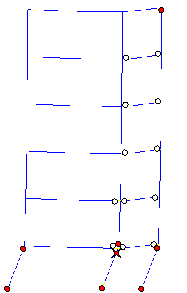
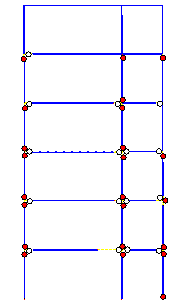
A comparison between Figures 10 and 11 reveals
that when the influence of slabs is considered, the damage in columns is more
severe than the damage in beams. This failure mode is closer to the actual
seismic damage. However, although the actual collapse began from the tops
of bottom storey columns, the predicted collapse begins from the feet of columns
in the bottom storey. Consequently, a more detailed analysis is still needed
for the bottom storey of the building.
3.2 Micro-macro-scale hybrid model
Both Macro-model A and Macro-model B predict
damage to be more severe at the feet of columns in the bottom storey than
at their tops. This differs from the actual seismic damage. A preliminary
analysis revealed that a possible reason for this difference is that in both
Macro-model A and Macro-model B, the column feet are fixed to the foundation,
even though the actual rotational stiffness of single footings of this type
cannot be infinite.
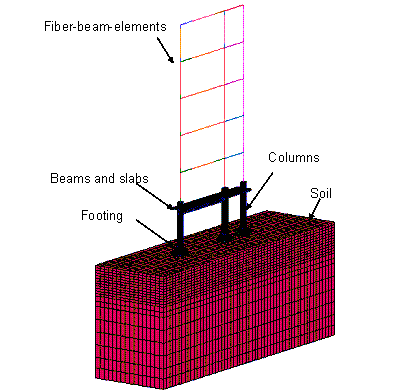
Therefore, a micro-macro-scale hybrid model
(referred as Hybrid-model in Table 1) was proposed to give a more detailed
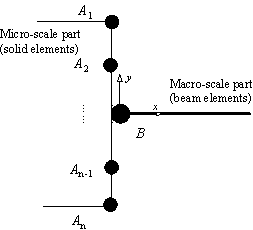
simulation of the bottom storey frame and the footings (Figure 12), and also
to balance accuracy with computational workload.
In the micro-macro-scale hybrid model, the
critical parts that may control the collapse of the frame, such as the beams,
the columns, the slabs in the bottom storey, the footings and the soil, are
modelled with micro-scale continuum elements, while the remaining parts are
still modelled with the same fibre-beam-elements as those in Macro-model B.
In the micro-scale part, concrete is modelled
with 3-dimensional solid elements. The compressive and tensile behaviour of
concrete is modelled using the elasto-plastic constitutive law and the smeared
crack model, respectively, which are provided by MSC.MARC (MSC 2005, Lu et
al. 2005). The equivalent uniaxial stress-strain relationship of concrete
is the same as the backbone curve shown in Figure 8a. The longitudinal reinforcements
and stirrups are modelled with truss elements whose stress-strain relationships
are the same as the one shown in Figure 9. The ˇăINSERTˇ± function provided
by MSC.MARC software (MSC, 2005) is used to maintain the displacement compatibility
between the rebar and the concrete elements. Also, the width of the floor
slabs in the micro-scale part is equal to 6 times the thickness of the slabs.
The width of the foundation soil is 5 times the width of the footing. The
interaction between the footings and soil is simulated with a contact algorithm,
which can transfer pressure through the interface and open when there is tensile
force at the interface (MSC, 2005).
3.2.1 Interface between the micro-scale part and the macro-scale part
The interfacial model proposed by Lu et
al. (2008c) was adopted to maintain deformation compatibility between
the solid elements in the micro-scale part and the beam elements in the macro-scale
part. To build up the interface, three useful functions provided by MSC.MARC
were used (user defined nodal coordinates, RBE2 nodal ties and UFORM user
subroutine (MSC, 2005). This interfacial model can avoid unnecessary stress
concentrations. The details of this interfacial connection method are introduced
in Appendix A of this paper.
3.2.2 Simulation results of micro-macro-scale hybrid model
The NS+UD components of the Wenchuan Earthquake
ground motion mentioned in Section 3.1.4 were used as input to the Hybrid-model,
and the time-history curve of the roof displacement is shown in Figure 13.
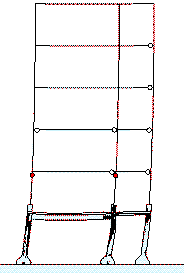
The plastic zone in the bottom storey before and during the collapse process
is shown in Figure 14. It can be seen that the columns have more plastic zones
than the beams, and collapse begins from the top of the middle-column in the
bottom storey. The results of the Hybrid-model, therefore are consistent with
the actual seismic damage.
There are obvious footing rotations in Figure
14, which will reduce the bending moment reactions at the column feet. Consequently,
there are more plastic zones at the tops of columns in the bottom storey,
and the collapse starts from the top of the middle-column in the bottom storey.
3.3 Fibre-beam-element model considering the influence of slabs and footing
rotations
The micro-macro-scale hybrid model provides
a powerful tool for explaining and analyzing the damage mechanism of Classroom
Building A. However, the relatively large computational workload of the Hybrid-model
makes it difficult to use for collapse fragility analysis, for which a large
number of statistical dynamic analyses are required. By contrast, both the
modelling and computing of the macro-scale fibre-beam-element model are much
easier. With proper parameters and boundary conditions, fibre-beam-element
models may also be able to accurately simulate the collapse processes of frames.
Hence, the macro-scale fibre-beam-element model (Macro-model B) was further
improved by supplementation with detailed structural information obtained
from the Hybrid-model. The improved fibre-beam-element model is able to simulate
the rotations of the footings, and yet maintain its simplicity in modelling
and computing.
Therefore, based on the results of the Hybrid-model,
to allow for the rotations of the footings, rotational springs were added
to the column feet of Macro-model B. This new model is referred to as Macro-model
C in Table 1. The stiffness of the rotational springs was determined from
a pushover analysis of the Hybrid-model, and found to be approximately 7000
kNm/rad. Because the factors that may influence the stiffness of the footing
rotations are very complicated, the value of rotational stiffness is specifically
discussed below.
The NS+UD components of the Wenchuan Earthquake
ground motion mentioned in Section 3.1.4 were used as input to Macro-model
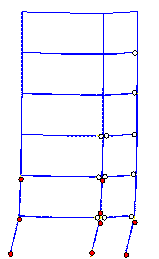
C. The time-history curve of the roof displacement and the failure mode are
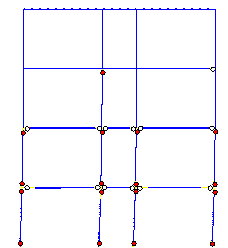
shown in Figures 13 and 15. From the curve comparison in Figure 13 and failure
mode comparison between Figure 14 and 15, it can be seen that the results
of Macro-model C and the Hybrid-model are in agreement with respect to: displacement
responses, plastic hinge positions, and the points where collapse starts.
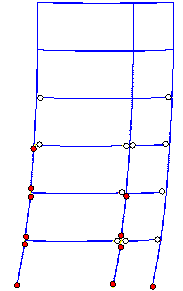
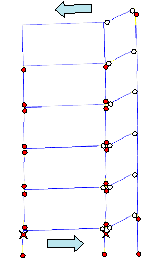
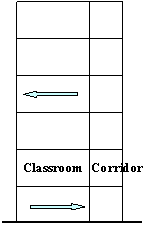
From Figure 15, it can be seen that collapse
starts from the middle-column in the bottom storey. When the collapse starts,
the deformation direction of the bottom storey inclines to the right side
(i.e., to the corridor side) (Figure 15a). Due to the combined bending moment
and axial force, the head of the middle-column in the bottom storey crushes
first (Figure 15b). After the failure of the middle-column, the axial force
in the left side-column (i.e., on the classroom side) suddenly increases,
followed by crushing at the top of the left side-column (Figure 15c). At this
moment, the collapse direction of the bottom storey still inclines to the
right (i.e., to the corridor side), as the arrow at the bottom of Figure 15c
indicates. It is interesting to note that because the gravity load on the
corridor is relatively small, the failure of the corridor side-columns is
delayed relative to the other columns. After failure of the two columns in
the bottom storey which support the classroom, the upper storeys incline to
the left (i.e., the classroom side), as the arrow at the top of Figure 15c
indicates. This simulated failure mode is very close to actual observations
(Figures 3, 4 and 5). In summary, the collapse of Classroom Building A can
be properly simulated with Macro-model C. Furthermore, the computational workload
of Macro-model C is much smaller than that for the Hybrid-model. Hence, Macro-model
C could be further used to predict the collapse fragility curve, requiring
a prodigious number of nonlinear time-history computations.
Because the factors that may influence the
stiffness of the footing rotations are very complicated, the estimated rotational
stiffness of 7000 kNm/rad, which is determined from the Hybrid-model, may
not precisely agree with the actual rotational stiffness. To account for this,
the rotational stiffness was adjusted by ˇŔ30%, which yielded a range from 4900 kNm/rad
to 9100 kNm/rad, in order to assess the sensitivity to assumed rotational
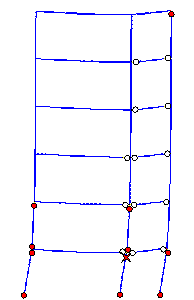
stiffness of the footings. The failure modes with different rotational stiffnesses
are shown in Figure 16. Comparing Figures 15 and 16, it can be seen that with
smaller rotational stiffnesses, the plastic hinges are concentrated more in
the bottom storey; whereas with greater rotational stiffness, more plastic
hinges appear in the second storey. Generally, however, the failure modes
in Figures 15 and 16 display no important differences. All the failures start
from the top of the middle-column in the bottom storey, and the plastic hinges
in the columns are more severe than those in the beams, in agreement with
the actual seismic damage. So it can be concluded that although the footing
rotational stiffness from the Hybrid-model may not be absolutely accurate,
its value does not seriously influence the collapse simulation. The footing
rotational stiffness of 7000 kNm/rad was used in later collapse fragility
assessments.
The failure modes shown in Figures 15 and
16 are obviously different from that shown in Figure 11 (the fixed column
feet in Macro-model B means that the rotational stiffness of the footings
is infinite). Consequently, in buildings such as Xuankou School with single
footings, rotation of the footings should not be ignored. The wide use of
fixed constraints assumption for the column feet, that is used in the design
computational models of RC frames may overestimate the restraint capacity
of the footings, which will result in incorrect predictions of internal force
and deformation.
From the above analysis, it can be concluded
that because of inappropriate modelling of the slabs and footing rotations
in the conventional design computational models used in China, actual seismic
damage is quite different from that assumed (Figure 10). Therefore, the computational
model used should be more carefully verified in future seismic designs.
Because Office Building H did not collapse
in the earthquake, and its seismic damage was relatively slight, only a macro-scale
fibre-beam-element model considering the influence of slabs and footing rotation
(i.e., Macro-model D in Table 1) was built to predict seismic response. The
EW+UD components of the Wenchuan Earthquake ground motion mentioned in Section
3.1.4 were used as input to Macro-model D according to the orientation of
the building. The deformation and the plastic hinge distributions are shown
in Figure 17. From Figure 17 it can be seen that the building avoids collapse
in the earthquake. The predicted plastic hinges of Office Building H are mostly
located in the bottom storeys, and are relatively slight. This prediction
is in agreement with the actual seismic damage.
When the NS+UD components of the Wenchuan
Earthquake ground motion (which were used to predict the collapse of the classroom
buildings) are used as input to Office Building H, Office Building H remains
able to avoid collapse. The corresponding deformation and plastic hinge distributions
in Office Building H are shown in Figure 18. There are more plastic hinges
in Figure 18 than in Figure 17. Consequently, the NS+UD components of the
Wenchuan Earthquake ground motion have a higher damage capacity than the EW+UD
components.
A comparison between the failure modes of
Classroom Building A (Figures 14 and 15) and Office Building H (Figures 17
and 18) shows that there are two disadvantages in the design of Classroom
Building A:
(1) The structure of Classroom Building A has
obvious weak points. The axial load ratios (the ratio between axial load and
axial resistance) of the columns in the bottom storey, particularly for the
middle-column in the bottom storey, are relatively large, resulting in a low
lateral deformation capacity. This is why failure always starts from the middle-column,
and the progressive collapse of the entire structure follows.
(2) Apart from the frame in the bottom storey,
most structural elements above the second storey have no plastic deformations
at the moment when Classroom Building A begins to collapse. Consequently,
the energy dissipation capacities of these structural elements do not effectively
develop. By contrast, Office Building H has more plastic hinges than Classroom
Building A, and the plastic hinges in Office Building H are more evenly distributed.
Thus, the global energy dissipation capacity of Office Building H is more
effectively developed.
|
![]()
![]()
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;
: Plastic
hinge in column; ![]() : Failure
point)
: Failure
point)![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;
: Plastic
hinge in column; ![]() : Failure
point)
: Failure
point)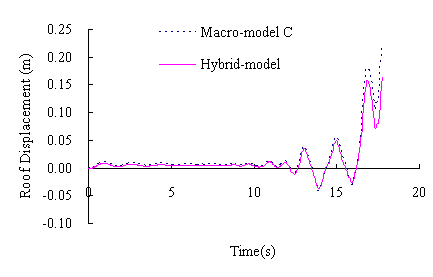
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;
: Plastic
hinge in column; ![]() : Failure
point)
: Failure
point)![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;
: Plastic
hinge in column; ![]() : Failure
point)
: Failure
point)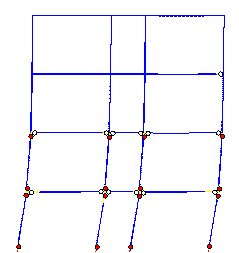
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;)
: Plastic
hinge in column;)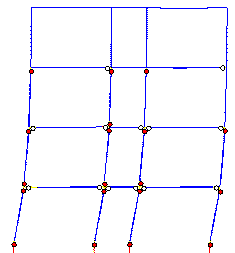
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;)
: Plastic
hinge in column;)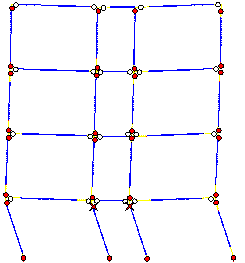
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column;
: Plastic
hinge in column; ![]() : Failure
point)
: Failure
point)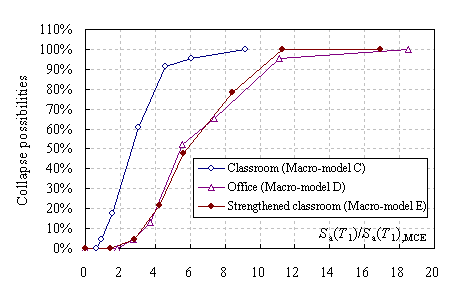
![]() : Plastic
hinge in beam;
: Plastic
hinge in beam; ![]() : Plastic
hinge in column)
: Plastic
hinge in column)