An improved tie force method for progressive collapse resistance design of reinforced concrete frame structures

Li Y, Lu XZ, Guan H, Ye LP

Download Full Text

Abstract: Progressive collapse of structures refers to local damage due to occasional and abnormal loads, which in turn leads to the development of a chain reaction mechanism and progressive and catastrophic failure. The tie force (TF) method is one of the major design techniques for resisting progressive collapse, whereby a statically indeterminate structure is designed through a locally simplified determinate structure by assumed failure mode. The method is also adopted by the BS8110-1:1997, Eurocode 1, and DoD 2005. Due to the overly simplified analytical model used in the current practical codes, it is necessary to further investigate the reliability of the code predictions. In this research, a numerical study on two reinforced concrete (RC) frame structures demonstrates that the current TF method is inadequate in increasing the progressive collapse resistance. In view of this, the fundamental principles inherent in the current TF method are examined in some detail. It is found that the current method fails to consider such important factors as load redistribution in three dimensions, dynamic effect, and internal force correction. As such, an improved TF method is proposed in this study. The applicability and reliability of the proposed method is verified through numerical design examples.

doi:10.1016/j.engstruct.2011.06.017

1.    Introduction

Progressive collapse of structures refers to a local damage due to occasional and abnormal event such as gas explosions, bombing attack and vehicular collisions. The local damage causes a subsequent chain reaction mechanism spreading throughout the entire structure which in turn leads to a catastrophic collapse. In general, progressive collapse of structures is characterized by a disproportion in size between a triggering event and the resulting collapse [1].

Since the 1968 partial collapse of the London¡¯s Ronan Point apartment tower, many nations have started investigations on progressive collapse resistance and published a series of design codes, specifications and guidelines. These include the British Standard and Regulation [2-4], Eurocode [5-6], NBCC [7], ASCE7-05 [8], ACI318 [9], GSA 2003 [10] and DoD 2005 [11]. Moore [12] investigated two building cases under occasional event and the study shows that progressive collapse resistance can be effectively improved by the UK provisions. Nevertheless, the current design codes and guidelines are not considered to completely satisfy the progressive collapse design requirements. In this regard, Dusenberry [13] suggested that further research is necessary to aid better understanding of the mechanisms of progressive collapse resistance of structures. This may include further study of the strength and ductility of structural elements and systems under limit state. From conceptual point of view, Nair [14] described three approaches to enhance progressive collapse resistance of structures, viz increasing redundancy (or alternate load paths), local resistance and interconnection (or continuity). Nair [14] also identified that the current international codes and standards focus primarily on the redundancy increase with little emphasise on the remaining two approaches. In the area of conceptual study, Starossek [15] suggested that progressive collapse of structures can be classified into six types, viz. the pancake, zipper, domino, section, instability and mixed types; and different treatments should be used for different types of collapse. In investigating analysis and design methods for progressive collapse resistance, Izzuddin et al. [16] proposed a simplified approach to progressive collapse assessment of steel-framed multi-storey buildings and Vlassis et al. [17] developed a new design-oriented methodology considering impact from failed floors.

In the current codes of practice, the tie force (TF) method is one of the two quantitative methods for progressive collapse design. The other is the alternate path (AP) method, which can be classified into linear elastic static, linear elastic dynamic, nonlinear static and nonlinear dynamic approaches. In the TF method, the ties between the structural members must satisfy the strength requirement to ensure structural integrity and the capacity of alternate load paths. The method simplifies the actual indeterminate structure to a locally determinate one with hinge-connected members, by which a minimum level of connection/tie force can be approximated. As such, complicated iterative computation is avoided. This makes the method simple in calculation and its analysis procedure can be easily standardized. According to Moore [12], the UK Building Research Establishment (BRE) has conducted a series of quarter-scale tests to verify the effectiveness and reliability of the TF method. Liu et al. [18] and Abruzzo et al. [19], on the other hand, have demonstrated in their respective studies that inadequacies do exist in the current TF method for progressive collapse design of steel and reinforced concrete frame structures. Moreover, the necessity of developing an improved TF method has been recommended by the DoD 2005 [11].

In this paper, the current TF method is firstly reviewed. To examine the effect of using the current TF method, a finite element solution is compared with the results of a published laboratory test on the collapse of a planar frame. This is followed by an in-depth study of the collapse mechanism of two reinforced concrete frame structures designed by the current TF method. The analysis results demonstrate the vulnerability of the structures to progressive collapse. The key elements in the current TF method are the two approaches for calculating the basic tie strength which is found to greatly influence the progressive collapse resistance capacity. One approach is related to the number of stories and the other, based on the assumed failure mode. These two approaches are examined in some detail in this study which reveals that the basic tie strength associated with the storey numbers is unable to truly reflect the capacity of progressive collapse resistance of frame structures and therefore should not be recommended. The tie strength based on the assumed limit state failure mode, on the other hand, is overly simplified without taking into account such important factors as load redistribution mechanisms in space, dynamic effect and internal force correction. Recognizing the abovementioned inadequacies in the current TF method, this study aims to improve the calculation model for the basic tie strength and propose a corresponding design procedure. The reliability of the proposed technique is verified through collapse analysis of the same frame structures re-designed using the improved TF method.

2.    The Current TF method

2.1. Background

The TF method was first recommended in the British Standard [2-4] shortly after the Ronan Point event. This is followed by the Eurocode [5-6] which employs a similar tie force model and formulas. Recognizing a sufficient similarity between the US and British construction practices, the DoD 2005 [11] directly adopts the specifications of the British Standard with a suggestion of possible amendment based on further investigation [11]. In this study, the TF method as specified in the British Standard is studied in some detail for collapse resistance design of RC frame structures.

2.2. Basic provisions

In the TF method, the structural elements are assumed to be mechanically tied together thereby enhancing continuity, ductility, and development of alternate load paths. Tie forces are typically provided by the existing structural elements and connections, which are designed using conventional procedures to carry the standard loads imposed upon the structure. According to the location and function, the ties are classified into four types, viz internal, peripheral, ties to columns and walls, as well as vertical ties. The load paths of various types of ties are required to be the shortest while maintaining continuity and the required tie strength must be satisfied.

2.3. Basic tie strength

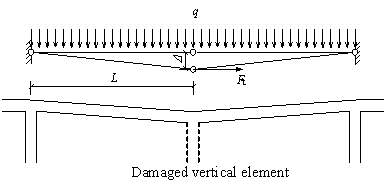
The current TF method is based on the basic tie strength F_t which is the minimum tensile force required for progressive collapse resistance. The strength of the four types of ties is obtained by multiplying the basic tie strength by a modification factor. As a result, the basic tie strength plays a highly important role in the entire TF methodology. In the current codes and standards, the basic tie strength is determined from the lesser of: (1) 4n_o+20 kN/m, where n_o is the number of stories in a structure, and (2) 60 kN/m. The first value is an empirical one from structural importance viewpoint. Using this value, structures with more stories would have more serious consequences due to progressive collapse. This thus leads to a larger requirement on the level of tie forces. The second value is obtained according to the following method - the failure mode of horizontal members, exhibiting a catenary behaviour, is assumed to effectively provide the required tie strength under limit state. It is believed that the horizontal members are able to function through catenary action thereby avoiding collapse. In such way, the complex indeterminate structure can be analyzed by transferring it locally into a determinate one at the location of a damaged vertical element, i.e. column. The analytical diagram for calculating the basic tie strength is illustrated in Figure 1 below.

From Figure 1,

where F_t is the total tensile force at mid-span; q is the uniformly distributed load applied to the top of the beam; L is the span length of the beam and ¦¤ is the allowable deflection. Substituting typical values of L=5 m, q=5 kN/m² and ¦¤=L/5 yields F_t=60 kN/m.

3.    Simulation of Progressive Collapse and Analysis of Failure Mechanism

In this study, the analysis of progressive collapse is based on the finite element method. The results of a published laboratory test on a reinforced concrete planar frame are used to verify the numerical solution. Further, the collapse mechanism of the planar frame tested is also examined.

3.1. Finite element analysis

The fiber beam model THUFIBER [20] previously developed by the authors is used herein in conjunction with a commercial finite element software MSC.MARC [21] to simulate the collapse of a reinforced concrete planar frame tested by Yi et al. [22]. Through comparison with the test results, the reliability of using THUFIBER in collapse simulation is verified.

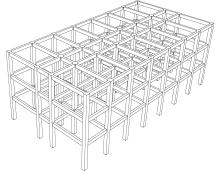
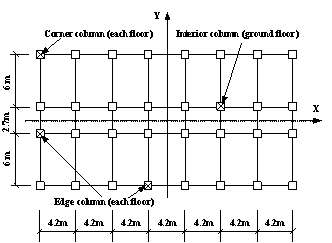
The four-span and three-story planar frame structure tested by Yi et al. [22] is shown in Figure 2, with detailed dimensions and test setup. In the experiment, a constant point load was applied to the top of the frame through a hydraulic jack. The removed/failed middle column in the ground floor, representing a collapse situation, was replaced by a passively loaded hydraulic jack. When the upper jack was balanced with load, the lower jack started to unload, by which the process of column removal can be replicated.

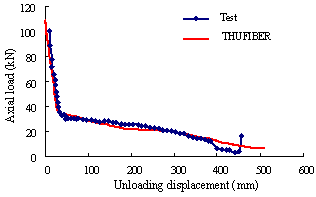
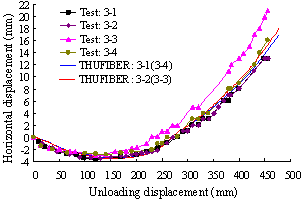
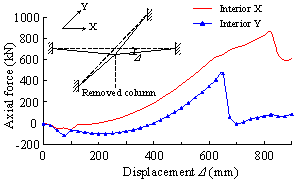
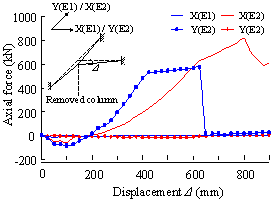
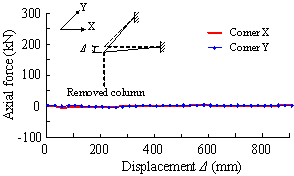
Figure 3(a) presents a comparison between the test results and the THUFIBER solution on the axial load versus the unloading displacement of the failed middle column. It is evident that the THUFIBER prediction is accurate. Shown in Figure 3(b) are the predicted horizontal displacements of the columns at first floor level affected by the downward displacement of the failed middle column. Again a good agreement with the test results is achieved, in particular at points 3-1 and 3-2.

3.2. Analysis of collapse and failure mechanism

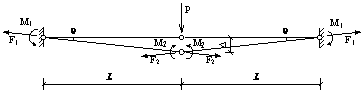
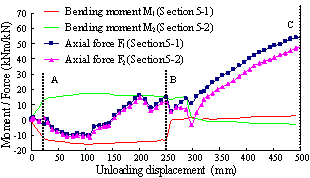
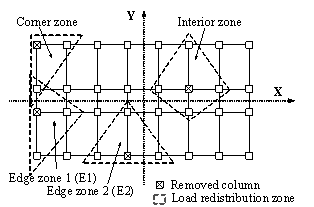
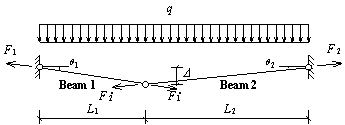
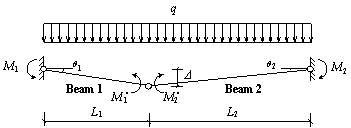
Shown in Figure 4(a) is the analytical diagram of the first floor beams supported directly by the failed middle column (see Figure 2). It should be noted that by virtue of symmetry, the axial forces at plastic hinges are identical at both beam ends (i.e. F₁). This is also true for the axial forces at plastic hinges at mid-span (i.e. F₂) as well as the moments (M₁ and M₂). Figure 4(b) presents the THUFIBER predictions of the internal forces (moments and axial forces) of the beam versus the unloading displacement of the failed middle column. Note also that due to symmetry, only the results of the left span (Sections 5-1 and 5-2 in Figure 2) are compared and reported herein.

A further examination of Figures 4(b) reveals that the load-carrying process of the beams can be classified into three stages:

(1)   Linear elastic stage (region 0A) - During this stage, the beam is restrained by the horizontal displacement and its cross-section is under the state of combined compression-bending. At the end of this stage, plastic hinges develop at the beam ends. The beam relies completely on the end moments in resisting the load.

(2)   Plastic hinge developing stage (region AB) - plastic hinges undergo relatively large rotation due to an increase in the applied load. At this stage, large vertical deformation develops in the first floor beams and the outward horizontal restraints at beam ends release gradually. The internal force status of the beam cross-section also gradually changes from compression-bending to tension-bending when the middle column displacement reaches 150 mm. The applied load is now resisted by both the beam-end moments (in a large proportion) and the axial forces. This is because the vertical component of the tensile force is small due to the small magnitudes of the resultant as well as the deflection of the beam.

(3)   Catenary action stage (region BC) - with continued increase in the applied load, the bending capacity at plastic hinges reduces dramatically thereby further increasing the deflection of the beam. At this stage, the applied load is carried by the beam, through tensile reinforcement, following a catenary action. With an increase in displacement, the vertical component of the beam axial force also increases. This leads to a further increase in load-carrying capacity until system collapses at point C.

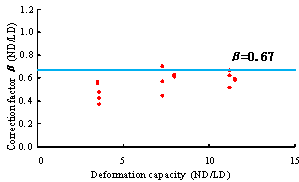
Based on the above discussion of the three stages, it can be summarised that the applied load is initially resisted by the beam-end moments (so-called ¡°beam action¡±) and then the axial forces (so-called ¡°catenary action¡±). The change-over phase of the two actions occurs at around Point B, as shown in Figure 4(b). Yi et al. [22]¡¯s experimental work reveals that the ¡°beam action¡± under small deformation and the ¡°catenary action¡± under large deformation can both be employed as a control state in collapse resistance design. However the relationships between deformation and ¡°action¡± has not been quantified for general cases. It is therefore necessary to discuss in some detail the ultimate deformation for beam action and catenary action.

3.3. Ultimate deformation for beam action and catenary action

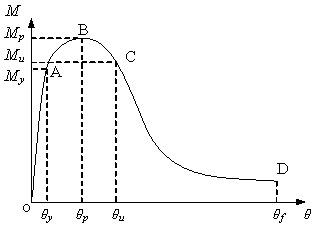
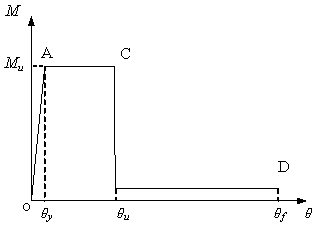
A typical moment-curvature relationship of a plastic hinge is presented in Figure 5(a). Corresponding to the ultimate moment M_u which is a 15% reduction of the maximum moment M_p, the rotation is defined as the ultimate rotation ¦¦_u. According to the statistics on plastic hinge rotations provided by Xu [23] who summarised the test results of a total of 154 beams failed in flexural, the average yield rotation ¦¦_y and the average ultimate rotation ¦¦_u of a plastic hinge are 0.34¡° and 3.4¡° respectively. The corresponding deflections ¦¤ of the beam are 0.006L and 0.06L respectively, while ¦¤ and L are demonstrated in Figure 4(a). A simplified moment-curvature relationship of a plastic hinge is presented in Figure 5(b). It should be noted that the tie force of beams, upon losing flexural capacity due to larger rotation than ¦¦_u, can be provided by tensile reinforcements until reaching fracture rotation ¦¦_f. DoD2005 [11] recommends that for beams with a span-depth ratio greater than 5 in structures of medium to high safety classification, ¦¦_f of a plastic hinge should be taken as 12º which is equivalent to 0.213L of the beam deflection. In the laboratory test of Yi et al. [22], ¦¦_f was found to be 10.3º which is equivalent to 0.182L of the beam deflection. A ¦¦_f of an equivalent deflection 0.2L is suggested in the current TF method [4, 6, 11]. Based on the above discussion, the corresponding ultimate deformations for beam and catenary actions are set to be 0.06L and 0.2L, respectively.

4.    Verification of Design Capacity Using the Current TF Method

The reliability of the current TF method as specified in the British standard is verified herein. This is done through examination of progressive collapse resistance capacities of two reinforced concrete frame structures designed using the current TF and the normal design methodologies. Note that the normal design refers to seismic design without consideration of TF requirement. The analysis of the frame models is performed using THUFIBER.

4.1. Details of the frame structures

Presented in Figure 6 are the perspective and plan views of a 3-storey and an 8-storey RC space frame structures, designed for the seismic intensity of 8 degree, with design peak ground acceleration of 0.2g, as specified in Chinese seismic design code [24]. This intensity is equivalent to Zone IIB, according to Uniform Building Code 1997 (UBC) [25]. Also shown in Figure 6(c) are the locations and floor levels of the removed columns. For the purpose of comparison, all the design parameters except the storey numbers are kept the same for both structures.

4.2. Analysis assumption

In the current TF design, the horizontal tie strength is calculated based on the floor width and is considered to be either distributed over the floor slab or concentrated on the beam [11]. In this study, a similar method to the sample calculation given in the Appendix of DoD 2005 [11] is adopted, where only the lateral-resisting system of the frame is modeled and horizontal tie reinforcements are assumed to be clustered in beams only. Another important consideration of such a treatment is that, in practice some of the floor slabs (e.g. precast and composite slabs) are unable to offer adequate tie strength. As a result, the slab contribution can be conservatively accounted for in the analysis. In addition, the basic tie strength is taken as the lesser of the two specified values determined on the basis of two different principles, as outlined in Section 2.3. The reliability of using these two values in the design is also investigated.

4.3. Evaluation of progressive collapse resistance capacity

Referring to GSA 2003 [9] and DoD 2005 [11], the process of element removal follows a top-down sequence. As illustrated in Figure 6(c), the middle column in the X- and Y-directions and the corner column of each floor are considered to be removed. For the ground floor, also removed is the interior column. Note that only one column is removed in each analysis. In the nonlinear time history analysis, an adequate time period of 3s is set so that the structural collapse, should it take place, can be reached. The detailed analysis procedure is outlined below:

(1)     Before element removal, the structure is in a static equilibrium under the applied vertical load;

(2)     Remove one structural element (i.e. selected column) by instantaneously deactivating the corresponding element in the finite element model, thereby releasing the internal forces of the removed element [21];

(3)     Analyze the structure up to failure or to a steady state. The failure criterion of a beam element is that the steel fiber is ¡°killed¡± when its ultimate strain is reached. If all the steel fibers on an element cross-section are ¡°killed¡±, the corresponding element is then considered failed. Also used as a supplementary failure criterion is the ultimate deflection of 0.2L (as discussed in Section 3.3) at the removed column joint.

4.4. Analysis results and discussion

Summarised in Tables 1 and 2 are the results of collapse analysis upon column removal for the 3- and 8-storey frames, respectively. Both the normal seismic design and current TF methods are used and the column removal is assumed to occur at various locations (see Figure 6(c)).

It can be found that the current TF method is unable to significantly enhance the progressive collapse resistance of the RC frame structures. For the 3-storey frame (Table 1), the structural responses (collapse or non-collapse) are identical with and without using the TF design method, except for the case of interior column removal in the 1^st (ground) floor. Similar results are also found for the 8-storey frame (Table 2) where the two design methods yield completely identical responses.

Table 1. Collapse status of 3-storey frame with normal and TF designs

Note: F_t in kN/m; C ¨C collapse; NC ¨C non-collapse; ¡°-¡±¨C not applicable

Table 2. Collapse status of 8-storey frame with normal and TF designs

Note: F_t in kN/m; C ¨C collapse; NC ¨C non-collapse; ¡°-¡±¨Cnot applicable

As discussed in Section 2.3, the basic tie strength plays a key role in the current TF method. One of the two basic tie strength values, F_t=4n_o+20 kN/m, is an empirical value without any theoretical verification. As indicated in Table 2 for the 8-storey frame, removing of columns in the higher stories (4^th and 5^th-8^th for the corner column; 5^th-8^th for the middle column in the X-direction) results in a higher possibility of structural collapse. This is because the residual frame offers less alternate load paths. On the other hand, when the 1^st floor columns (corner column and middle column in the X-direction) are removed, collapse has occurred in the 3-storey frame (Table 1). This is however not the case for the 8-storey frame (Table 2). The simulated collapse results imply that if more stories exist above the removed columns, the redundancy of the residual structure is higher because more remaining beams are available to carry the applied load. The overall system is thereby stronger in progressive collapse resistance. The results further suggest that progressive collapse resistance is enhanced by developing alternate load paths which is in direct proportion to the number of stories of frames. This is under the condition that the remaining structural configurations, such as plan layout, are identical. The above discussion implies that the design demand for progressive collapse decreases with an increase in storey numbers. However the empirical value of basic tie strength F_t=4n_o+20 kN/m in the current TF method suggests otherwise ¨C higher design demand with more storey numbers. This further reveals that the use of value F_t=4n_o+20 kN/m reflects primarily the serious consequence of progressive collapse of higher storey frames rather than their actual collapse resistance capacity.

Tables 3 and 4 respectively list the total amount of longitudinal steel reinforcement (SA) required for beams for each floor of the 3- and 8-storey frames. Three design methods are used viz. the normal seismic design (with no consideration on progressive collapse), the AP design and the current TF design. Also presented in the tables are the percentage increase (Ic) of steel amount as compared to the normal design, as well as the total SA and Ic for the entire frame. It should be noted that the nonlinear dynamic AP method specified in DoD 2005 [11] is generally accepted as an accurate approach for progressive collapse design. As such, the AP method is used first to gradually increase the amount of steel until reaching a non-collapse state of the system. Such steel amount is then used as a threshold requirement for comparison. For the 3-storey frame, Table 3 shows that the total Ic (i.e. 2.36%) resulted from the TF design (with F_t=4n_o+20 kN/m) is much less than that of the actual minimum requirement (17.85%). For a frame with low number of stories (n_o is small), F_t=4n_o+20 kN/m is inevitably smaller than F_t=60 kN/m. Hence a smaller amount of steel is required should the lesser value of 4n_o+20 kN/m and 60 kN/m is chosen for the TF design. This unfortunately leads to an underestimation of the design demand for low-rise frames.

For the 8-storey frame, Table 4 demonstrates that the total Ic (3.9%) due to the TF design (with F_t=4n_o+20 kN/m) exceeds that of the actual minimum requirement (2.47%). The increase in steel amount is particularly evident for 1^st-5^th floors whereas the AP design suggests nil requirement. However insufficient tie reinforcement amount are found for the top three floors of the frame as compared to the AP design, making the beams thereof the weakest components for preventing progressive collapse. This suggests that the empirical value for basic tie strength (F_t=4n_o+20 kN/m) also fails in estimating the steel demand and location for frames with large number of stories.

Table 3. Comparison of steel amount in beams of 3-storey frame with different designs

Note: F_t in kN/m; SA ¨C steel amount in ton; Ic ¨C increase as compared to normal design (%)

Table 4. Comparison of steel amount in beams of 8-storey frame with different designs

Note: F_t in kN/m; SA ¨C steel amount in ton; Ic ¨C increase as compared to normal design (%)

Similar to the above discussion, the other value of basic tie strength in the current TF method, F_t=60 kN/m, also shows certain level of deficiency in improving progressive collapse resistance as demonstrated in Tables 3 and 4. For the 3-storey frame (Table 3), the total Ic (i.e. 15.49%) due to F_t=60 kN/m is closer to the minimum requirement (17.85%), as compared to that due to F_t=4n_o+20 kN/m (2.36%). This is because F_t=60 kN/m, based on the catenary action theory instead of practical experience, is considered to be a more reasonable value. Nevertheless, the TF method (even based on F_t=60 kN/m) still fails to offer adequate prevention to progressive collapse, as indicated in Table 1.

For the 8-storey frame (Table 4), the total Ic (i.e. 6.36%) based on the TF design with F_t=60 kN/m is much more than the minimum requirement (2.47%). This, together with the individual Ic for individual floor, further confirms the inadequacy of the basic tie strength value F_t=60 kN/m in that additional reinforcement is not provided at appropriate locations for effective enhancement for progressive collapse. In view of the above, the underlining problems and issues in the current TF method are necessary to be addressed and rectified. This leads to the improvement to the current TF method which is presented in the following section.

5.    Improvement to the current TF method

5.1. Underlining problems in the current TF method

The numerical analysis presented in Section 4 demonstrates that the current TF method is unable to effectively enhance the capacity of progressive collapse resistance of frame structures. Firstly, the basic tie strength requirement F_t=4n_o+20 kN/m, relating to storey number only, is not a reliable theoretical value. The method thus inevitably underestimates the progressive collapse resistance demand for low-rise frame structures. Secondly, the basic tie strength model (Figure 1), based on the catenary action assumption, has also failed in arranging the additional tie reinforcement in an appropriate manner. As a result, the first empirical value F_t=4n_o+20 kN/m is not considered in the present improvement work. On the other hand, the second value of basic tie strength F_t=60 kN/m is modified due to its rationality, to a certain extent, in terms of catenary action principle.

5.2. Issues in the basic tie strength model

The main issues associated with the basic tie strength model are discussed in the following three aspects.

5.2.1.   Load redistribution in space

Load redistribution is a three-dimensional phenomenon in actual structures. However such a characteristic is not considered in the planar catenary model of the current TF method in calculating the basic tie strength. Two questions are posed when dealing with load redistribution characteristics in space: (1) in resisting the external load, what mechanism (beam action or catenary action) the beams exhibit when they run in different directions? (2) what is the distribution of the external load carried by each individual beam through displacement compatibility? Moreover, what is the relationship between the load carrying capacity of beams and the external load? It should be noted that both questions are related to the location of the initial damaged column. For a typical layout of a frame structure, Figure 7(a) illustrates three load redistribution zones: interior, edge and corner zones. If a column is collapsed (removed), the beams in the corresponding load redistribution zones will then act as alternate paths in carrying the applied load.

For the first question, it should be noted that not all the beams can provide effective tie strength through catenary action. This is demonstrated by modeling the three load distribution zones shown in Figure 7(a) as substructures. The dimensions and material properties of the substructures are identical to those adopted for the 3- and 8-storey frames. All the beams are reinforced with four 25 mm longitudinal bars at top and bottom sections, respectively. The corresponding axial (tie) force of beams versus the joint displacement are presented in Figures 7(b) to (d).

Results indicate that only the continuous beams, fully constrained at both ends, are able to provide adequate support reactions and axial tie forces. This is the case for the interior zone, as evident in Figure 7(b). This figure also indicates that when the joint displacement D reaches the ultimate displacement of the shortest beam in the Y-direction, the said beam is then considered to have failed. Subsequently, the remaining beams in the X-direction continue to offer tie strength up to failure. For the edge zones shown in Figure 7(c), the tie forces are provided by the beams along the frame periphery only due to the constraints at both ends. The perpendicular cantilever beams provide nil tie force. This is the same for the beams in the corner zone (Figure 7(d)) where a free end exists. It should be pointed out that beams with little or no tie force still contribute to progressive collapse resistance. As discussed in Section 3.2, under small deformation, ¡°beam action¡± is dominant in providing anti-collapse bearing capacity. Such an action is transformed into ¡°catenary action¡± upon approaching ultimate deformation. For the two beams in the corner zone and the cantilever beam in the edge zone, where the ¡°beam action¡± does not require horizontal constraint at beam ends, the contribution to progressive collapse resistance by the ¡°beam action¡± instead of ¡°catenary action¡± can be guaranteed at small deformation stages. Therefore, for the interior and corner zones, the progressive collapse resistance can be assessed respectively by the catenary and beam actions. For the edge zone, on the other hand, the resistance should be assessed by the greater of resistances under ¡°catenary action¡± for the periphery beams and the ¡°beam action¡±, for all the connecting beams in both directions.

For the second question, the distribution of the external load carried by each individual beam is discussed for catenary and beam actions, respectively. The corresponding analytical diagrams representing a general case are demonstrated in Figure 8.

For the ¡°catenary action¡±, the tie strength demand of each of the connecting beams should take the value of the actual tie force when the allowable deflection of the shortest beam is reached. This is because for connecting beams, the plastic hinges at beam ends reach their ultimate rotation at different times due to different span lengths. The shortest beam usually damages first and fails in providing tie strength. This results in an overload on the remaining beams due to load redistribution, which in turn leads to a system failure. In the current TF method, however, the influence of different span lengths in different directions for connecting beams and hence their interactions are not considered. The tie strength demands in beams in different directions are calculated individually. This obviously differs from the actual catenary mechanism.

Assuming the shortest beam in space is Beam 1, as shown in Figure 8(a). Its ultimate state is defined by the vertical deflection ¦¤ reaching the allowance value L₁/5, where L₁ is the span length of Beam 1. Satisfying the equilibrium of the horizontal components of the beam axial forces leads to

Considering ¦¤=L₁/5 and L₁<L_2£¬Eq. (2) can be simplified as

Satisfying the equilibrium of the vertical components of the beam axial forces leads to

Re-arranging Eq. (4) yields

Assuming the shortest beam in the perpendicular direction is Beam 3 with a span length L₃>L₁, a similar relationship between the tie strengths in Beams 3 and 4 can also be obtained, as expressed in Eq. (6). This is under the condition of displacement compatibility where the joint is considered to have reached the same ultimate deflection ¦¤=L₁/5.

Similarly, the relationship between F₃ and the applied uniformly distributed load  in the perpendicular direction can be reached. Or,

Eqs. (3) and (5), and (6) and (7) describe the relationship between the tie force and the applied load in the two orthogonal directions, respectively, when the joint deflection reaches its ultimate value of L₁/5. It is therefore recommended, in designing tie strengths for dual-direction connecting beams, that the lower bound of the required tie strength and the applied load should satisfy Eqs. (3), (5), (6) and (7).

For the ¡°beam action¡± shown in Figure 8(b), the equilibrium of the plastic hinge bending moments and the applied load yields, for each beam (assuming L₁<L₂),

A local damage of the joint is likely caused by the collapsed column. This in turn minimizes the moment capacity at around the joint. Hence, the bending moments at joints, i.e. M₁¡± and M₂¡± can be conservatively neglected. Eqs. (8) and (9) can then be reduced to Eqs. (10) and (11) where the applied load is resisted by the plastic hinge moments at beam ends only.

The ¡°beam action¡± also requires that the two beams must satisfy displacement compatibility. According to Section 3.3, when the joint deflection ¦¤ reaches 0.06L₁, the ultimate rotation ¦¦_u of the shorter beam (Beam 1) is attained. With a further increase in the joint deflection, the moment resistance capacity of the shorter beam reduces rapidly. This is followed by the load redistribution which eventually leads to failure of the other beam (Beam 2). This behavior is similar to the ¡°catenary action¡±. However, unlike the ¡°catenary action¡±, the ¡°beam action¡± indicates that the rotation of the longer beam (Beam 2) has exceeded ¦¦_y (equivalent to 0.006L₂) when ¦¤=0.06L₁. This is true unless L₂>10L₁. In most practical cases, however, L₂<10L₁. Therefore the rotations of both beams are expected to fall within region AC where the ultimate moment M_u is reached. This is indicated in Figure 5(b). This implies that both beams are able to provide their respective maximum moment capacity.

Similar to Eqs. (10) and (11), the beam-end moments of the orthogonal beams (Beams 3 and 4) can be expressed as

Finally, the required tie strengths for connecting beams in space, assessed by the ¡°beam-action¡±, must satisfy Eqs. (10) to (13).

5.2.2    Dynamic effect

The current TF method is a static design method which is an idealized assumption. Upon initial and instantaneous damage of a column, the remaining structural members reach a new stage of equilibrium. This is indeed a dynamic process. It is worth noting that the maximum internal forces (axial tie forces or moments) are practically larger than those obtained through static analysis. As such, an unsafe solution is resulted should the dynamic effect is ignored. This problem is handled in the GSA 2003 [10] and DoD 2005 [11] for the static AP method by using a dynamic amplification coefficient, a of 2.0 applied to the static load to simulate the dynamic effect. It should be noted that such a coefficient is influenced not only by the dynamic effect but also the nonlinear behaviour. In the present study, however, these two aspects are considered separately for clarity in discussion. The coefficient a, expressed herein by the ratio of linear static (LS) and linear dynamic (LD) responses, is verified through analysis of the 3-storey frame structure. Figure 9 shows the linear dynamic amplification coefficients a for different column removal cases in terms of internal force versus displacement responses. It can be seen that the code specified coefficient, 2.0, is slightly conservative. Tsai and Lin [26] have also verified, through nonlinear static analysis, that the amplification coefficient, expressed by the ratio of nonlinear static and nonlinear dynamic responses, also produces conservative estimation for collapse resistance if the dynamic amplification factor is set to 2.0.

5.2.3    Internal force correction ¨C nonlinear effect

In the current analytical model, the tie strength is obtained based on the analysis of sub-structures (tie elements) isolated from the entire structure. This however differs from reality in that the substructures are connected to the adjacent structures in the entire system, thereby causing elasto-plastic load redistribution among all structural members. When considering the substructures in isolation, the calculated internal forces (axial tie forces or moments) are inevitably larger.

In GSA 2003 [10], when the linear elastic AP method is used, the calculated internal forces (axial tie forces or moments) are required to be corrected to reflect the actual nonlinear structural and material behavior. This is done by examining a demand-to-capacity ratio, expressed as , where Q_UD is the acting force (demand) determined in structural elements and Q_CE is the expected ultimate (capacity), un-factored capacity. Using the DCR criteria of the linear elastic approach, structural elements that have DCR values exceeding 2.0 (for typical structural configurations) or 1.5 (for atypical configurations) are considered to be severely damaged or collapsed [10]. In other words, the correction of calculated internal forces can be achieved by satisfying Q_CE¡»0.5Q_UD and Q_CE¡»0.67Q_UD for typical and atypical structural configurations, respectively.

In the improved TF method, the correction factor ¦±, taking into account the nonlinear effect, is represented by the ratio of internal forces in nonlinear dynamic (ND) and linear dynamic (LD) analyses. This factor is verified through the 3-storey frame under different column removal conditions. Presented in Figure 10 are the internal force correction factors ¦± versus the deformation capacity. Also given in the figure is a line representing ¦±= 0.67 as specified in GSA 2003 [10]. It is evident that this value covers almost all the column removal cases. This ¦± value is thus used in further analysis verifying the improved TF method.

This study takes into account both dynamic effect and nonlinear behaviour through the consideration of the dynamic amplification coefficient a (=2.0) and the internal force correction factor ¦± (= 0.67), respectively. Verification using the 3-storey frame indicates that the multiple of a and ¦± is 1.34, which is less than 2.0. This finding is consistent with the suggestion by Ruth et al. [27] in that the dynamic amplification factor is closer to 1.5 for nonlinear responding systems than the factor 2.0 specified in the GSA requirements.

Figure 10. Correction factor ¦± for 3-storey frame under different column removal conditions

5.3. Improved TF Method

Based on the above discussions on the underlining problems and issues in the current TF method, an improved analytical model for basic tie strength is proposed herein.

5.3.1.     Basic assumptions

Suggested below are the basic assumptions for frame structures:

(1)     Upon initial damage of a column, the bridging capacities of the connecting beams perform in ¡°beam action¡± (i.e. moment capacity at plastic hinges at beam ends) or ¡°catenary action¡± (i.e. tensile strength offered by the longitudinal reinforcement throughout the beam);

(2)     For the ¡°beam action¡±, only the negative moment at beam end plastic hinges is considered which is convenient and conservative. The positive moment at mid-span is ignored;

(3)     The ¡°catenary action¡± is only applicable for continuous beams with longitudinal reinforcement throughout. It is inappropriate otherwise for cases like beams connecting to corner columns;

(4)     The tie members must have adequate deformation and shear strength capacities which can be ensured by satisfying the minimum design requirements.

5.3.2.     Analysis method and procedure

The detailed analysis method and procedure leading to the improved TF method are outlined below:

Step (1): A substructure is established by isolating the connecting beams for different load redistribution zones from the entire structure, as shown in Figure 7(a).

Step (2): Applied uniformly distributed floor surface load S to the substructure.

where G is the dead load (kN/m²); Q is the live load (kN/m²); and ¦° is the dynamic amplification factor set as 2. According to the floor arrangement (one-way or two-way slab), S can be converted to uniformly distributed load q acting on each beam (see Figure 8).

Step (3): For interior joints, the tie forces in the orthogonal beams are assessed by the ¡°catenary action¡± only. This is because the carrying capacities of the beams acting in the ¡°catenary action¡± are found to be larger than those in the ¡°beam action¡±. This can be confirmed by Yi [22]¡¯s experiment where the latter is about 70% of the former. For corner joints, the beam-end moment capacities for the orthogonal beams are assessed by the ¡°beam action¡±. For edge joints, on the other hand, the resistance should be assessed by the greater of resistances under ¡°catenary action¡± for the periphery beams and the ¡°beam action¡±, for all the connecting beams in both directions.

For the ¡°catenary action¡±, the tie force capacities F_i and F_j for Beams i and j, respectively, must satisfy the following:

where b = 0.67 is the internal force correction factor; q is the uniformly distributed load acting on the beam; L_i and L_j are respectively the span lengths of Beams i and j in specific directions; ¦¤ is the allowable limit of the joint deflection which equals 1/5 of the shortest span length of the connecting beams.

For the ¡°beam action¡±, the beam-end moment capacity M_i must satisfy the following:

where L_i is the span length of the corresponding beam.

6.    Verification of the Improved TF Method

The improved TF method proposed in this study is verified using the present 8-storey frame structure. Compared in Table 5 are the total steel amount SA in beams required for each floor resulted from the current and improved TF design methods. Also presented in the table are the percentage increase (Ic) of steel amount as compared to the normal design, as well as the total SA and Ic for the entire frame. Results indicate that the required steel amount is slightly higher in the improved TF design. Such a slight increase in SA (with Ic = 6.53%) has resulted in the structure satisfying the requirement of progressive collapse resistance where no collapse occurs. Also can be seen is a more appropriate distribution of steel for each floor, in particular the top three floors, as compared to the current TF design.

Table 5. Comparison of steel amount in beams of 8-storey frame with different designs

Note: F_t in kN/m; SA ¨C steel amount in ton; Ic ¨C increase as compared to normal design (%)

To verify the applicability and reliability of the improved TF method for lower seismic intensity designs, the same 8-storey frame is re-designed for seismic intensities of 7 and 6 degrees with other parameters unchanged. The respective design accelerations are 0.1g and 0.05g. Similarly, the seismic design loads of intensity 6 and 7 degrees in China are generally equivalent to 2/3 of that of Zone I and Zone IIB respectively, as specified in UBC 1997 [25]. The new designs using the improved TF method have been found to both satisfy the requirement of progressive collapse resistance. Compared to the normal design, Table 6 indicates that the frames designed for different seismic intensities require, with different percentages, an increase in the steel amount (Ic = 6.53%, 26.12% and 40.68% for 8, 7 and 6 degrees, respectively). This suggests that the improved TF method is effective for different seismic designs in that the structural redundancy is increased which is beneficial for progressive collapse resistance. In addition, when the design is based on higher seismic intensity, a smaller increase in steel should be required to satisfy progressive collapse resistance. This is also verified by the analysis results in that Ic decreases when the seismic design requirement becomes higher.

Table 6. Comparison of steel amount in beams of 8-storey frame designed for different seismic intensity

Note: SA ¨C steel amount in ton; Ic ¨C increase as compared to normal design (%); Normal ¨C normal seismic design; ITF ¨C improved TF design

7.    Concluding Remarks

The tie force (TF) method is one of the most popular techniques for progressive collapse resistance design. This method is simple in calculation and easy in standardization as compared to the nonlinear dynamic AP method which requires more specialized input of designers. Despite such advantages, the current TF method is lacking in its fundamental principles for calculating the basic tie strength. The inadequacies of the current TF method are discussed in some detail in the present study through numerical analysis of published test specimen and two RC space frames. An improved TF method is subsequently proposed taken into account such important factors as load redistribution in three dimensions, dynamic effect, and internal force correction. The proposed method has proven to be effective in replicating the actual mechanism of structural members. The method is also reliable for improving progressive collapse resistance for frames designed under different seismic intensities.

Acknowledgement

The authors are grateful for the financial support received from the National Science Foundation of China (No. 90815025), the Tsinghua University Research Funds (No. 2010THZ02-1) and the Program for New Century Excellent Talents in University.

References

[1]    Ellingwood BR. Mitigating risk from abnormal loads and progressive collapse. J Perf Constr Fac, ASCE 2006; 20(4):315-23.

[2]    Office of the Deputy Prime Minister. The building regulations 2000, Part A, Schedule 1: A3, Disproportionate collapse. London, United Kingdom, 2004.

[3]    British Standard Institute. BS6399: Loading for buildings, Part 1: Code of practice for dead and imposed loads. London, United Kingdom, 1996.

[4]    British Standard Institute. BS8110: Structural use of concrete, Part 1: Code of practice for design and construction, United Kingdom, 1997.

[5]    European Committee for Standardization. EN 1991-1-7:2006, Eurocode 1: Actions on structures. Part 1-7: General Actions - Accidental actions. Brussels, Belgium, 2006.

[6]    European Committee for Standardization. EN 1992-1-1:2004, Eurocode 2: Design of concrete structures. Part 1: General rules and rules for buildings. Brussels, Belgium, 2004.

[7]    Canadian Commission on Building and fire Codes, National Research Council of Canada. National Building Code of Canada, Ottawa, Canada, 2005.

[8]    American Society of Civil Engineers (ASCE). Minimum design loads for buildings and other structures (ASCE7-05), Reston, VA, 2005.

[9]    American Concrete Institute (ACI). Building code requirements for structural concreteand commentary (ACI 318m-08). Detroit, Michigan, 2008.

[10]  United States General Services Administration (GSA). Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects, Washington D.C., 2003.

[11]  Department of Defense (DoD). Unified Facilities Criteria (UFC): Design of Structures to Resist Progressive Collapse, Washington D.C., 2005.

[12]  Moore DB. The UK and European regulations for accidental actions. Proc Workshop on Prevention of Progressive Collapse, National Institute of Building Sciences, Washington D.C., 2002.

[13]  Dusenberry D. Review of existing guidelines and provisions related to progressive collapse. Proc Workshop on Prevention of Progressive Collapse, National Institute of Building Sciences, Washington, D.C., 2002

[14]  Nair RS. Preventing Disproportionate Collapse. J Perf Constr Fac, ASCE 2006; 20(4):309-14.

[15]  Starossek U. Typology of progressive collapse. Eng Struct, 2007; 29(9):2302-07.

[16]  Izzuddin BA, Vlassis AG, Elghazouli AY, Nethercot DA. Progressive collapse of multi-storey buildings due to sudden column loss-Part I: Simplified assessment framework. Eng Struct, 2008; 30(5):1308-18.

[17]  Vlassis AG, Izzuddin BA, Elghazouli AY, Nethercot DA. Progressive collapse of multi-storey buildings due to failed floor impact. Eng Struct, 2009; 31(7):1522-34.

[18]  Liu R, Davison B, Tyas A. A study of progressive collapse in multistory steel frames. Proceeding of ASCE/SEI Structures Conference, New York, 2005.

[19]  Abruzzo J, Matta A, Panariello G. Study of mitigation strategies for progressive collapse of a reinforced concrete commercial building. J Perf Constr Fac, ASCE 2006; 20(4):384-90.

[20]  Lu XZ, Li Y, Ye LP, Liang Y. Application of fiber model for progressive collapse analysis of reinforced concrete frames. Proc 12th Int Conf on Computing in Civil and Building Engineering, Oct. 2008, Beijing, CDROM.

[21]  MSC.Marc Volume A: Theory and User Information. MSC Software Corp, Santa Ana, Calif, 2005.

[22]  Yi WJ, He QF, Xiao Y, Kunnath SK. Experimental Study on Progressive Collapse-Resistant Behavior of Reinforced Concrete Frame Structures. ACI Structural Journal, 2008; 105(4):433-9.

[23]  Xu FJ. Studies on Displacement-based Seismic Design Methodology of Reinforced Concrete Frame-Core Wall Structures. Beijing: PhD thesis of Tsinghua University. 2006 (in Chinese).

[24]  The Ministry of Construction of the People's Republic of China. Code for seismic design of buildings. (GB50011-2001), Beijing, 2001.

[25]  International Code Council. Uniform Building Code, Volume 2, 1997.

[26]  Tsai MH, Lin BH. Investigation of progressive collapse resistance and inelastic response for an earthquake-resistant RC building subjected to column failure. Eng Struct, 2008; 30(12):3619-28.

[27] Ruth P, Marchand K A, Williamson EB. Static equivalency in progressive collapse alternate path analysis: Reducing conservatism while retaining structural integrity. J Perf Constr Fac, ASCE 2006; 20(4):349-64.

Appendix. Notation

The following symbols are used in this paper: