INTRODUCTION
In recent years, more and more large-scale structures (e.g., high-rise buildings, super-tall buildings, large-span bridges and high dams) are being designed and built worldwide. Concurrently, research on the seismic behavior of large-scale structures has become increasingly common, owing to the important social function of these structures and the frequent occurrence of earthquakes. In addition, research to date indicates that numerical simulation, using finite element (FE) analysis, is an effective method of investigating the nonlinear seismic behavior of such structures (Lu et al. 2011, 2013a; Xu et al. 2013; Li et al. 2014; Xie et al. 2014a). Among existing FE software, OpenSees, an open-source FE program, has been widely used because it is versatile, extensible and shareable (McKenna et al. 2009).
A multi-layer shell element, based on the principles of composite material mechanics, has been developed in OpenSees for shear walls, core tubes and floor slabs, which are important components of large-scale structures (Lu et al. 2013b; Xie et al. 2014a, 2014b). This multi-layer shell element has been applied in investigating the seismic behavior of super-tall buildings and large-span bridges, providing useful references and an effective tool for further research on the seismic behavior of large-scale structures. However, the abovementioned research also indicated that the computational efficiency of OpenSees based on CPU computing cannot satisfy the demand for numerical simulation of large-scale structures. This restricts further investigation on the seismic behavior of such structures using this software package.
Recently, GPU have been rapidly developed and applied in the general computing field, due to their powerful parallel computing capability and low cost (Owens et al. 2007). Further, seismic damage simulations of urban areas have been conducted by Lu et al. (2014a) using GPU/CPU cooperative computing. Their benchmark cases indicate that the computing efficiency of GPU could be up to almost 40 times that of a traditional CPU. Accordingly, a GPU may have the potential to provide a high-performance alternative for the seismic performance analysis of large-scale structures based on OpenSees.
In this study, two new parallel-iterative solvers for the sparse SOEs are proposed and implemented in OpenSees, based on GPU-powered high-performance computing. The nonlinear time history analysis (THA) of a 141.8 m frame-core tube building and a super-tall building (the Shanghai Tower with a height of 632 m) are performed using the proposed solvers. In comparison with the existing CPU-based SparseSYM solver in OpenSees, the speedup ratio using the proposed solver is up to 9 to 15, with high accuracy in result. The outcome of this study can provide an effective computing technology for numerical analysis of the seismic behavior of large-scale structures.
COMPUTING METHOD
Solvers for the Sparse SOEs in OpenSees
A critical issue for nonlinear THA, using OpenSees, is how to define the system of equations (SOE), which includes two basic classes: the Linear System of Equation (LinearSOE) class and the Linear System of Equation Solver (LinearSOESolver) class. The LinearSOE class and the LinearSOESolver class determine the storage and solution method of the SOE, respectively.
In the LinearSOE class, the SOE is usually composed of mass, stiffness and damping matrices. For large-scale structure models using beam and shell elements, the stiffness matrix and mass matrix usually exhibit significant sparse characteristics. The damping matrix will be also sparse, if classical Rayleigh damping is adopted. Hence, a storage method suitable for sparse SOE is required in the LinearSOE class.
The LinearSOESolver class in OpenSees (Version 2.4.3) integrates three types of sparse SOEs, namely: SuperLU SOE, UmfPack SOE and SparseSYM SOE. For these sparse SOEs, direct methods are generally adopted, such as triangular and elimination decomposition. However, direct methods are difficult to be highly parallelized. Based on CPU computing, only a few solvers can be paralleled with a low efficiency. The direct method is also not suitable for GPU-based parallel computing. Therefore, a new and efficient solver for the sparse SOEs is required in the LinearSOESolver class.
GPU-based Solvers for the Sparse SOEs in OpenSees
GPUs have powerful floating point operations and parallel computing capabilities, which are very favorable for large-scale computational problems. However, according to the above analysis, the solvers for the sparse SOEs in OpenSees are not suitable for parallel processing using a GPU. Therefore, it is necessary to develop a new solver for the sparse SOEs in OpenSees, which is more suitable for GPU-based parallel processing. To improve the performance of the GPU-based solver and retain compatibility with the original computing programs in OpenSees, the solver is developed based on the following rules:
(1) The iterative method including the conjugate gradient (CG) algorithm, Bi-CG algorithm and GMRES algorithm is used to maximize the parallel computing ability of the GPU.
(2) The SOE class (corresponding to the LinearSOE class) and the Solver class (corresponding to the LinearSOESolver class) are designed separately. The SOE class is designed inheriting the LinearSOE class, to improve the compatibility of the solver.
(3) The solving function in the Solver class is designed in the form of a dynamic-link library (DLL) to improve extensibility, which is convenient for modification.
Figure 1 illustrates the specific solving process of GPU-accelerated solvers. The matrix is integrated in CPU, and then copied into the graphics memory to perform parallel computing. Finally, the results are returned into CPU for subsequent computing.
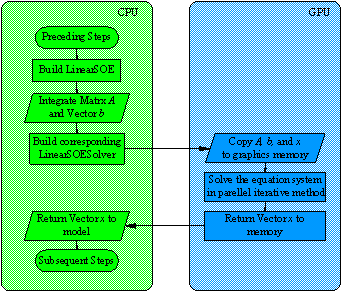
Figure 1. Flow chart of GPU-based solvers for the sparse SOEs
There exists several storage formats for sparse matrices. Among these, the compressed sparse row (CSR) format is commonly adopted. This storage format can quickly convert into the coordinate (COO) format, with less storage space than alternatives. Some useful matrix characteristic values, such as the number of non-zero elements in a row of the matrix, can be quickly obtained. In addition, the CSR format is convenient for the parallel computing of matrix multiplication and vector-matrix multiplication. Hence, this format is used to store the sparse matrices in this study. A SparseGenRowLinSOE class is provided in OpenSees, which can store sparse matrices in the CSR format. Therefore, this class is used directly as the designed SOE class in this work.
The designed Solver class should be written in a language suitable for GPU computing. Therefore, two GPU-accelerated solving libraries for the sparse SOEs, based on Compute Unified Device Architecture (CUDA) (NVIDA, 2014a), are adopted, namely: (1) CulaSparse, which is a linear algebra function library (Humphrey et al. 2010) and (2) CuSP, which is an open source library for sparse linear algebra (NVIDIA, 2014b). The corresponding scripts of CuSP are provided in detail at http://opensees.berkeley.edu/wiki/index.php/Cusp. The corresponding source codes that illustrate the implementation procedure of these two solvers in detail are available at the website of OpenSees (PEER, 2014). This will facilitate the reproduction of this research.
CASE STUDY
A performance benchmark is conducted for the proposed GPU-based solvers. Two structural models are adopted in this benchmark, named TBI2N model and Shanghai Tower model, respectively. The TBI2N model is a frame-core tube building designed according to the Chinese building design codes for the TBI program (H = 141.8 m) (Lu et al. 2014b). It contains 23,945 nodes, 23,024 fiber-beam elements and 16,032 multi-layer shell elements, as shown in Figure 2(a). The OpenSees model is freely assessable (Lu, 2014c), which can be conveniently shared and reused in the research community. The Shanghai Tower model (H = 623 m) (Lu et al. 2011) contains 53,006 nodes, 48,774 fiber-beam elements and 39,315 multi-layer shell elements, as shown in Figure 2(b).
The El-Centro EW ground motion is adopted to perform the nonlinear THA. According to the design conditions, peak ground acceleration (PGA) values of 1000 gal and 400 gal are selected for the TBI2N and Shanghai Tower models, respectively, to investigate the strong nonlinear behavior they would be subjected to in extremely rare earthquakes. Detailed information of the GPU and CPU hardware platforms and their respective solvers are illustrated in Table 1.
|
|
|
|
(a) the TBI2N model |
(b) the Shanghai Tower model |
|
Figure 2. Benchmark models |
|
Table 1. Hardware platform and solvers for the comparison
|
Platform |
Hardware |
Solvers |
|
CPU computing |
Intel Core i7-3970X 3.5GHz |
SparseSYM |
|
GPU computing |
Intel Core i7-4770X 3.4GHz & NVIDIA Geforce GTX Titan |
CulaSparse Solver & CuSP Solver |
|
|
|
(a) TBI2N model |
|
|
|
(b) Shanghai Tower model |
|
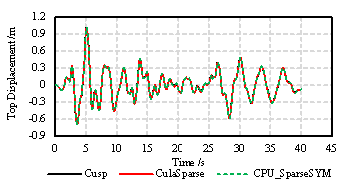
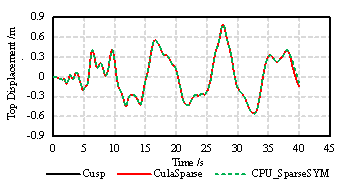
Figure 3. Comparison of top displacement time history curves |
Table 2. Computing Time and speedup ratio of Three Solvers
|
Platform |
Solvers |
Computing time of the TBI2N model |
Speedup ratio |
Computing time of the Shanghai Tower model |
Speedup ratio |
|
CPU |
SparseSYM |
168 h |
\ |
409 h |
\ |
|
GPU |
CulaSparseSolver |
18 h |
9.33 |
38 h |
10.76 |
|
CuSPSolver |
11 h |
15.27 |
27.5 h |
14.87 |
Based on above platforms, the performances of the three solvers (two GPU-based solvers and one CPU-based solver) are compared. Figure 3 presents the comparison of top displacement time-history curves. As shown in Figure 3, there are nearly negligible differences between the results of the CPU solver and the GPU solvers, which is acceptable. Table 2 shows the comparison of the computing times and the speed-up ratios. The speed-up ratio is up to 9-15 times by using the two proposed GPU-based solvers. Evidently, the GPU-based solvers in OpenSees exhibit significant reliability and high efficiency for the nonlinear THA of large-scale structures.
CONCLUSIONS
In this study, two new parallel-iterative solvers for the sparse SOEs are proposed and implemented in OpenSees, based on two GPU-based libraries (CuSP and CulaSparse). The THAs of two high-rise buildings are conducted using the two proposed GPU-based solvers and an existing CPU-based solver. The results indicate that GPU-based solvers have a good agreement with CPU-based solver in accuracy. Furthermore, a speedup ratio of 9-15 times is achieved using the proposed solvers. This work provides an important computing technology for the high performance analysis of large-scale structures based on OpenSees.
ACKNOWLEDGEMENTS
The study is supported by National Key Technology R&D Program (No. 2013BAJ08B02), National Natural Science Foundation of China (No. 91315301Ł¬51378299), and Beijing Natural Science Foundation (No. 8142024). The authors also acknowledge Bo Han and Mengke Li for their contributions to this work.
REFERENCES
Humphrey, J. R., Price, D. K., Spagnoli, K. E., Paolini, A. L., and Kelmelis, E. J. (2010). ˇ°CULA: hybrid GPU accelerated linear algebra routines.ˇ± SPIE Defense, Security, and Sensing. International Society for Optics and Photonics, 770502-770502.
Lu, X. Z., Xie, L. L., Huang, Y. L., Lin, K. Q., Xiong, C., and Han, B. (2013b). ˇ°Nonlinear simulation of super tall building and large span bridges based on OpenSees.ˇ± http://www.luxinzheng.net/download/OpenSees_Workshop/LuXinzheng.pdf >(Feb. 6, 2015).
Lu, X. Z., Li, M. K., Lu, X., and Ye, L. P. (2014b). ˇ°A comparison of the seismic design of tall RC frame-core tube structures in China and the United States.ˇ± Proceedings of the 10th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Anchorage, AK, doi: 10.4231/D3DZ03252.
Lu, X. Z. (2014c). ˇ°OpenSees Tall Buildings.ˇ± http://www.luxinzheng.net/download/OpenSeesTallBuildings.zip >(Feb. 6, 2015).
McKenna, F., Scott. M. H., and Fenves, G. L. (2009). ˇ°Nonlinear finite-element analysis software architecture using object composition.ˇ± J. Comput. Civil Eng., 24(1), 95-107.
NVIDIA (2014a). ˇ°CUDA C programming guide.ˇ± http://docs.NVIDIA.com/cuda/pdf/CUDA_C_Programming_Guide.pdf >(Feb. 6, 2015).
NVIDIA (2014b). ˇ°CuSP Home Page.ˇ± http://cusplibrary.github.io/ >(Feb. 6, 2015).
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M., Kr¨ąger, J., Lefohn, A. E., and Purcell, T. J. (2007). ˇ°A survey of general-purpose computation on graphics hardware.ˇ± Comput. Graph. Forum., 26, 80¨C113.
PEER (2014). ˇ°Subversion Repositories.ˇ± http://opensees.berkeley.edu/WebSVN/listing.php?repname=OpenSees&path=%2Ftrunk%2FSRC >(Feb. 6, 2015).
Xie, L. L., Huang, Y. L., Lu, X. Z., Lin, K. Q., and Ye, L. P. (2014a). ˇ°Elasto-plastic analysis for super tall RC frame-core tube structures based on OpenSees.ˇ± Engineering Mechanics, 31(1), 64-71. (in Chinese)
Xie, L. L., Lu, X., Lu, X. Z., Huang, Y. L., and Ye, L. P. (2014b). ˇ°Multi-layer shell element for shear walls in OpenSees.ˇ± Computing in Civil and Building Engineering, ASCE, 1190-1197.