1 Introduction

Progressive collapse is a complex mechanical process of structural systems, including failure and fracture of the structural members, change of load transfer path in the systems and impact and contact of separated and falling structural components (Starossek 2007). The objective of progressive collapse design is to prevent the propagation of failure throughout the structural members induced by unbalanced gravity load subsequent to a damage of local members under accidental loading (GSA 2003; DoD 2005; DoD 2010). To achieve this objective, the critical state of a building structure under large deformations is analyzed in which the initial failure of the local members is considered, however no consequent damage of the remaining structure is permitted (DoD 2010). Based on this concept, the impact-contact issue in progressive collapse can be neglected to simplify practical engineering design processes. At the initial stage of collapse (e.g., when the local members fail), the residual structural components that can provide the resistance to the unbalanced gravity load is referred to as the ¡°collapse-resisting substructure¡±, as shown in Figure 1. The collapse resistance demand of the substructure, R, refers to its necessary capacity to prevent progressive collapse. If adequate resistance can be provided by the substructure, i.e. the collapse resistance demand is satisfied, further failure or collapse of the residual structural members can be prevented. Otherwise, subsequent damage will occur, which may trigger a progressive collapse of the entire structure.

The existing numerical (Li et al. 2011) and experimental (Yi et al. 2008; Sadek et al. 2011) studies have proven that progressive collapses are resisted by the beam mechanism (i.e., via the bending moments M at the beam ends) for RC frame structures undergoing small deformations (see Figure 1), and by the catenary mechanism (i.e., the axial forces throughout the framed beams) for structures undergoing large deformations.

The linear static (LS) alternative path (AP) method regulated in the existing codes (GSA 2003; DoD 2005; DoD 2010) performs a static analysis for overall structural systems in which small geometric deformations and linear elastic materials are considered. Hence, using the LS AP method, the resistance demand R and the bending moments M under the beam mechanism can be obtained for RC frame structures. The LS AP method is a much simplified approach than the nonlinear dynamic (ND) AP method in which geometric and material nonlinearities and dynamic time histories must be considered. In this paper, the corresponding outcomes of the LS and ND AP methods are respectively referred to as the LS and ND demands, R_LS and R_ND. The LS demand R_LS calculated using the existing codes (GSA 2003; DoD 2005; DoD 2010), which is regarded as the preliminary results thereafter, must be corrected by multiplying a dynamic amplification factor (DAF) to approximate the actual ND demand R_ND, whereby the dynamic and nonlinear effects can be taken into consideration. A similar dynamic factor was also used in the simplified assessment of the safety of bridges (Chen et al, 2011a; Chen et al, 2011b).

Due to the implicit coupling effect of the structural nonlinear behaviour on the structural dynamic response, it is a difficult task to obtain an explicit expression for an accurate DAF based on the theory of nonlinear structural dynamics. To simplify the engineering design process, two correction factors with empirical values are specified in GSA2003 (GSA 2003) and DoD2005 (DoD 2005).  They are the DAF and the demand-capacity ratio (DCR). Note that, the recommended value of DAF of 2.0 is considered overly conservative when representing the dynamic effect with nonlinear behaviour (Ruth et al. 2006; Stevens et al. 2011; Khandelwal & El-Tawil 2011). Therefore, the DAF is further reduced by a DCR to better account for the effect of nonlinearity (GSA 2003). In DoD2010 (DoD 2010), the DAF for the LS analysis is classified into two types, a force-controlled DAF of 2.0 for brittle components and a deformation-controlled DAF for ductile components which is a ductility-related factor. The empirical expression of the deformation-controlled DAF in DoD2010 is obtained by fitting the numerical results of a large number of LS and ND analyses of a 3-storey and a 10-storey model structures (Marchand et al, 2009).

On the other hand, the energy method is very convenient to be used to derive a mathematic expression of the DAF if the substructure can be simplified to a single-degree-of-freedom (SDOF) equivalent (see Figure 1) of which the energy equation is considerably simple (Tsai 2010). Indeed the DAF for the nonlinear static (NS) analysis has been studied by Tasi (2010) and Izzuddin and Nethercot (2009) using the energy method.

In many countries, structures with sufficient ductility are commonly required in the existing design codes, such as the Chinese codes for concrete structures (MCPRC 2010a) and seismic design (MCPRC 2010b). Hence, it is more practical and cost-effective if a ductility-related DAF is used in the LS analysis. In this paper, the DAF for the LS analysis is evaluated for the progressive collapse design of ductile RC frame structures, based on the energy analysis of the SDOF equivalent representing the collapse-resisting substructure. The proposed analytical expression of the DAF is validated through a SDOF system, a 3-storey RC planar frame and an 8-storey 3-D RC frame model structures.

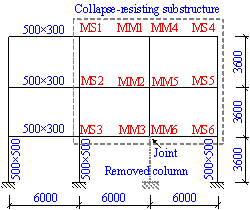
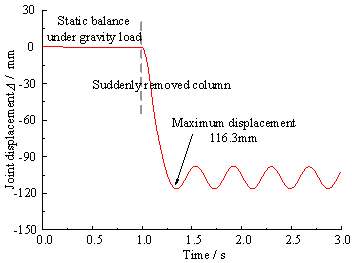
2 The analytical expression of the DAF in the LS analysis for ductile RC frames

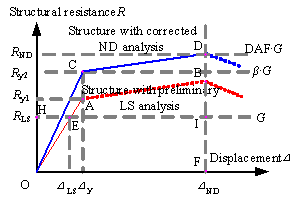
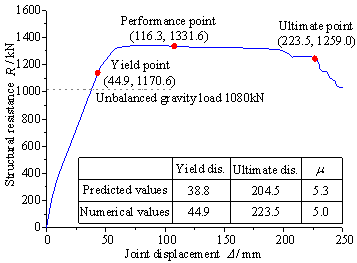
The LS and ND resistance demands for RC frame substructures under the beam mechanism is illustrated in Figure 2. The resistance curve of the substructures designed by the preliminary LS analysis is a polyline OAB in which the resistance after point A is neglected because the nonlinear behaviour is not considered in the analysis. The LS resistance demand, RLS, is represented by Point E, which satisfies the static equilibrium condition under an unbalanced gravity load G:

Furthermore, to prevent the occurrence of progressive collapse, an additional demand induced by the nonlinear and dynamic effects during the collapse process should also be satisfied. In practice, a DAF is used to conveniently correcting RLS to approximate the ND resistance demand, RND. The resistance curve of the corrected substructures is the polyline OCD in which the resistance after point D is neglected because the resistance at this stage may be less than the unbalanced gravity load G. In the practical design, a DAF of 2.0 implies that the yield strength Ry2 satisfies Ry2¡Ý2G. Moreover, if structural energy dissipations at the nonlinear stage (represented by line CD) are considered to contribute to the resistance of the substructure, the total resistance demand will be decreased, making the DAF less than 2.0. The minimum level of the ND resistance demand RND is represented by Point D which is the peak resistance of the substructure.

Based on the energy conservation principle, the energy dissipation of the substructures, i.e., the area under OCDF, should be equal to the work done by the unbalanced gravity load, i.e., the area under OHIF. The energy equilibrium equation is expressed as

where D_ND and D_y are the ND displacement demand and the yield displacement respectively.

The yield factor ¦Â of the substructures is defined as

Substituting R y2 from Equation (3) into Equation (2) yields

Considering Equation (1), the DAF for the LS analysis of ductile RC frame substructures can be calculated as

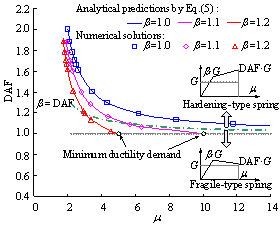
where ¦Ì=D ND/D y is the ductility factor of the RC frame substructures under the beam mechanism.

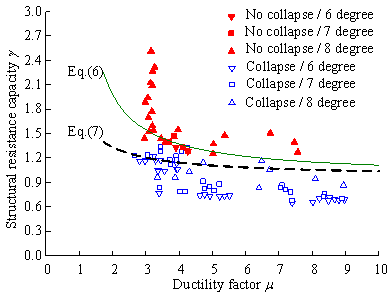
It should be noted that the DAF is obtained by an iterative process of calculation. This is because the value of ¦Â of the corrected substructure, which is required to calculate the DAF, is also unknown. Such an iterative process is detailed in Section 3.2. For practical design purposes, Equation (5) is further simplified as follows. The preliminary LS design has led to a substructure satisfying the requirement R y1¡ÝG = R LS, where R y1 is the yield strength of the substructure. Considering R y2> R y1, the yield factor becomes ¦Â>1. If ¦Â¡Ý2, the structure remains at the linear elastic stage subsequent to a local damage, and the solution is a linear dynamic demand R LD=2G. Thus, 1<¦Â<2 or 0<(2£­¦Â) <1. Equation (5) can be further simplified to provide a conservative solution by assuming ¦Â=1:

For general ductile RC frame structures, the ductility ratios of RC beams with different reinforcement arrangements, shear-span ratios and material and geometrical properties were suggested by Panagiotakos and Fardis (2001) and ASCE-41-06 (ASCE 2007). The ductility factor m of the substructures can then be calculated using the suggested values for RC beams, as detailed in Section 3.2.

It is worth noting that energy dissipation of structural damping is neglected in this study due to the following two reasons: (1) The potential energy of unsupported mass is mainly dissipated by structural members in the process of initial downward impact immediately after the removal of the vertical supporting structural member. Energy dissipation of structural damping during this monotonic process is much less than that during the cyclic process in which such energy dissipation must be considered (e.g., in seismic performance assessment). (2) A conservative DAF is obtained when neglecting energy dissipation of structural damping. This simplification was also adopted in other similar progressive collapse studies (Tasi 2010; Izzuddin and Nethercot 2009).

3 Numerical verification

Using the finite element method, three numerical examples are presented herein to validate the proposed DAF. Firstly, a SDOF system with bilinear resistance which is consistent with the resistance model used to establish the DAF in Figure 2, is further analyzed to verify the analytical expression of the DAF in Equation (5). Given that the SDOF system is simple in concept and application, it is therefore convenient to be used to examine various parameters in relation to the resistance curve to represent different types of frame structures, by which the relationships between the DAF and ¦Â or m can be evaluated. Following this, the process of calculating the ND demand using the DAFs in Equation (5) and Equation (6) is demonstrated via a 3-storey planar RC frame. Finally, the DAF proposed for practical designs (Equation (6)) is validated through an 8-storey 3-D frame structure. It should be noted that the proposed DAF is for resistance demand evaluations of the ductile RC frame structures under the beam mechanism. Hence only the mechanical behaviour associated with the beam mechanism is considered in these numerical studies.

3.1 SDOF system

The DAF described in Equation (5) is verified by a SDOF system, as shown in Figure 3. Initially the SDOF system is in a state of static equilibrium in which the lumped mass is supported by a horizontal constraint. Upon sudden removal of this constraint, a nonlinear dynamic analysis is conducted to calculate the ND force and displacement demands. Note in the figure that the mass and the support are connected by a bilinear spring representing the progressive collapse resistance of the system. Different nonlinear parameters of the spring are considered to evaluate the nonlinear effect on the resistance demand.

The validation results are illustrated in Figure 4, which indicates that the analytical predictions of Equation (5) are consistent with the numerical solutions for varying yield factors ¦Â. The numerical solution of DAF refers to as the ratio of the maximum force, F_max, of each spring during the dynamic collapse process which is considered as the ND demand, to the gravity load G which is considered as the LS demand, i.e. DAF= F_max /G. The ductility factor ¦Ì is the ratio of the maximum displacement D_ND in the ND analysis to the yield displacement D_y of the spring, i.e. ¦Ì=D_ND/D_y. It can be seen that the resistance demand decreases with an increase in the structural ductility, m. Two different types of bilinear springs are identified, namely, the hardening type and the fragile type. A dash-dot line representing ¦Â = DAF is also drawn in the figure. It provides a boundary between the structural demands using the hardening-type spring (above the line) and the softening-type spring (below the line). The results further reveal that the hardening-type systems have higher progressive collapse resistance than the fragile-type counterparts, and a larger ductility is required when the fragile-type systems are designed. The minimum ductility demand can also be calculated by setting DAF=1.0 in Equation (5), as shown in Figure 4.

3.2 3-storey planar RC frame model structure

The process to calculate the ND demand by using the proposed DAF is demonstrated through a 3-storey planar RC frame model structure. Figure 5 shows the dimensions of the structural elements and the location indexes of the beam ends within the substructure where the internal forces are to be analyzed. Note that MS and MM are referred to as the beam bending moments on the side and middle of the substructure span, respectively. Note also that the third column in the ground floor is to be removed suddenly to induce progressive collapse. The compressive strength of concrete and the yield strength of steel reinforcement are 20.1MPa and 335.0MPa respectively. The gravity load acting on the beams is set as 30kN/m.

The calculation process is summarized in the following four steps:

(1) The LS analysis is conducted first to calculate the LS demands of the model. The resulting bending moments and the required longitudinal reinforcement on the tension side of the beam end sections are listed in Table 1.

(2) The yield rotation and ultimate rotation (i.e., the rotation corresponding to the remarkable reduction of the bending moment) of the beams are calculated using Panagiotakos and Fardis (2001)¡¯ empirical equations which were established based on a database of more than 1000 tests on various of types of RC members including beams, columns and walls. The corresponding yield and ultimate displacements are obtained by multiplying the rotations to the span length. They are presented in Table 1 together with the yield and ultimate displacements of the joint (top of removed column, see Figure 5), which are the respective total average displacements of both beam ends.

(3) According to the study of Tasi (2010), the average value of the yield displacements of the two beam end types, i.e. MSs and MMs (see Figure 5), is defined as the yield displacement of the substructure. Whereas the ultimate displacement of the substructure is that of the shortest beam within the substructure (Li et al. 2011). This leads to the ductility factor of the substructure, ¦Ì, by dividing the ultimate displacement by the yield displacement, which equals 204.5/38.8=5.3.

(4) The DAF is then calculated by substituting ¦Ì obtained from Step (3) into Equation (6) resulting in DAF=1.23. It is subsequently used to correct the bending moments obtained in Step (1) to obtain the ND demands which are also given in Table 1. The longitudinal reinforcement on the tension side of the beam end sections is re-designed based on the ND demands.

  The corrected RC frame is numerically analyzed using a fiber-beam element model named THUFIBER, developed previously by the authors (Miao et al. 2011; Lu et al. 2013). THUFIBER takes into account complex interaction mechanisms of the internal forces at the beam sections and has robust material models considering both unloading and reloading paths. Published literatures show that RC frames exhibiting a flexural and axial failure behavior can be satisfactorily simulated using THUFIBER (Li et al. 2011; Miao et al. 2011; Lu et al. 2013). The corrected frame is analyzed herein by the ND AP method using THUFIBER and the time-domain displacement response of the frame is displayed in Figure 6. The maximum joint displacement after the column removal is found to be 116.3mm which is less than 1/5 the span length, as specified in the GSA and DoD codes (GSA 2003; DoD 2005; DoD 2010). This result suggests that the frame does not reach the collapse status.

Figure 7 illustrates the resistance curve of the corrected frame which is obtained using the pushdown method (Khandelwal 2008). The maximum displacement subsequent to column removal is found to be smaller than the ultimate displacement of the substructure, which indicates that the corrected frame has redundant capacity components. Such a redundancy is achieved because ¦Â=1 is assumed in Equation (6) leading to a conservative prediction of the DAF. If Equation (5) is used in Step (4) instead of using Equation (6), and an initial value of ¦Â (e.g., ¦Â=1) is assumed to obtain a DAF, by which the resistance demand and the yield strength (i.e., R y2) on the beam ends will be established. Subsequently, the values of ¦Â and DAF will be updated using Equation (3) and Equation (5). This iterative process is continued until the values of ¦Â and DAF converge to a set of solution with less redundancy. This process is obviously complicated and unsuitable for practical design purposes. As a result, a conservative prediction of DAF with ¦Â=1 is often considered accurate for practical designs that is validated in the next section.

Figure 7 also presents the empirically predicted values (Panagiotakos and Fardis 2001) of the yield and ultimate displacements and the ductility factor m of the RC substructure, which are in close agreement to the numerical values. This comparison demonstrates that the empirical equations can be used to calculate the DAF in the LS AP analysis for ductile RC frame structures.

3.3 8-Storey 3-D RC frame model structure

In order to verify the accuracy of Equation (6) for practical designs, an 8-storey 3-D RC frame model structure, shown in Figure 8, is analyzed using THUFIBER to better replicate practical situation. The structure is designed for three seismic intensities of 6, 7 and 8 degrees. The corresponding PGA (peak ground acceleration) values of the design earthquake (i.e., a 10% probability of exceedance over a 50-year interval) are 50 cm/s², 100 cm/s² and 200 cm/s^2, respectively. This results in three frame structures having different progressive collapse resistances due to different seismic design requirements. Other design parameters remain the same for the three structures, and other relevant details can be found elsewhere (Li et al. 2011). The ductility ratios of these structures as designed by the Chinese concrete (MCPRC 2010a) and seismic codes (MCPRC 2010b) are larger than 3.0.

The progressive collapse analysis is conducted by removing one column at a time. The concerned columns include a corner column, a typical interior column and two middle columns in the x- and y-directions of each floor. The three frame structures with one column removed are analysed using the nonlinear static pushdown method and the nonlinear dynamic time history method.

In the nonlinear static pushdown analysis, the ductility factor m and the structural resistance capacity, ¦Ã, of the substructure are evaluated, where ¦Ã is the ratio of the structural resistance under the ultimate deformation to the unbalanced gravity load. The corresponding DAF is calculated by substituting m into Equation (6). If ¦Ã ¡Ý DAF, the substructure is considered safe after the specified column is removed. However, if ¦Ã<DAF, a progressive collapse of the substructure is assumed to be triggered. Regardless of whether the progressive collapse demand of the substructure is satisfied or not, the prediction of the progressive collapse resistance demand can be verified by the nonlinear dynamic time history analysis, i.e., the ND AP analysis.

The values of ¦Ã for the three frame structures are displayed in Figure 9 using different legend marks, where the hollow and solid marks denote collapse and non-collapse scenarios according to the ND AP analysis, respectively. It is evident that the prediction of Equation (6), which is depicted by the solid line, accurately describes the structural demand for RC frame structures under the beam mechanism. The collapse and non-collapse scenarios are distinctly separated by the DAF calculated by Equation (6). This result confirms that Equation (6) provides a safe solution to DAF for engineering design purposes. In addition, Equation (6) is more practical than Equation (5) because the iterative process of calculating ¦Â and DAF is not required by Equation (6).

The lower bound of the theoretical DAF can be expressed as Equation (7) by assuming ¦Â=DAF in Equation (5), which means all components yield at the same time and the whole structural performs an elastic-perfectly plastic structural behavior:

It can be seen from Figure 9 that the lower bound of the theoretical DAF is unsafe, because the components in the real 3-dimensional structures may not yield and failure at same time. Hence, ¦Â=1 (Equation (6)) is recommended for the engineering design.

4 Conclusion

Evaluating an accurate resistance demand is a key issue in progressive collapse designs. The nonlinear dynamic (ND) resistance demand is the true demand for RC frame structures in progressive collapse; however, the direct calculation of the ND resistance demand, given both nonlinear and dynamic effects, is overly time-consuming and computationally costly. The existing design codes and current investigations all suggest that the ND resistance demand can be determined by correcting the easily obtainable LS resistance demand using a dynamic amplification factor (DAF). An empirical DAF for the LS design is regulated in DOD2010 for the ductile RC frames. Based on the energy method, this study has successfully proposed an analytical expression of the DAF for the LS analysis in progressive collapse designs of ductile RC frame structures. The DAF are validated through a SDOF system, a 3-storey planar RC frame and an 8-storey 3-D RC frame model structures. The numerical validation also demonstrates that the suggested simplified equation to calculate the DAF, i.e. Equation (6), provides a safe solution for the LS AP design of the ductile RC frame structures.

Acknowledgement

The authors are grateful for the financial support received from the National Basic Research Program of China (No. 2012CB719703), the National Science Foundation of China (No. 51222804, 51208011), the China & Beijing Postdoctoral Science Foundation (2012M510301, 2012ZZ-13) and the Research Program of Beijing Municipal Commission of Education (KM201310005025).