|
Conclusions
A collapse probability index is proposed in this paper. Taking into consideration
of all possible initial failure modes, the proposed index is thus independent
of the initial local failure and can evaluate the structural progressive collapse
resistance from the overall structural point of view. Based on this index,
the progressive collapse fragility curve is also proposed in this study. Such
a curve can reflect the redundant structural collapse resistance through the
variation of the collapse probability with the nominal gravity load. In addition,
to reduce the workload of the computation and analysis work, a simplified
method to obtain the progressive collapse fragility curve of RC frames is
proposed to meet the requirement of routine engineering design practice. Results
of the numerical examples suggest that the proposed index and simplified method
can provide a good assessment of the structural progressive collapse-resisting
performance of RC frames and that the obtained results agree well with the
theoretical analysis.
Acknowledgement
The
authors are grateful for the financial support received from the National
Basic Research Program of China (973 Program) (No. 2012CB719703), the National
Natural Science Foundation of China (No. 51578018) and the Australian Research
Council through an ARC Discovery Project (DP150100606).
References
Agarwal J, Blockley D and Woodman
N (2003) Vulnerability of structural systems. Structural Safety 25(3):
263-286.
Applied Technology Council (ATC)
(2009) Quantification of Building Seismic Performance Factors (FEMA
P695). Redwood City, CA: ATC.
Baker JW, Schubert M and Faber MH
(2008) On the assessment of robustness. Structural Safety 30(3): 253-267.
Bao Y and Kunnath SK (2010) Simplified
progressive collapse simulation of RC frame-wall structures. Engineering
Structures 32(10): 3153-3162.
Bao Y, Main JA, Lew HS, et al. (2014)
Robustness assessment of RC frame buildings under column loss scenarios. In:
Proceedings of the 2014 Structures Congress, Boston,
MA, 3-5 April, pp. 3153-3162. Reston, VA: ASCE.
Benjamin JR and Cornell CA (1970)
Probability, Statistics, and Decision for Civil Engineers. New York:
McGraw-Hill.
Department of Defense (DoD) (2010)
Unified Facilities Criteria (UFC): Design of Structures to Resist Progressive
Collapse. Washington, DC: DoD.
European Committee for Standardization
(ECS) (2006) Eurocode 1: Actions on structures. Part 1-7: General Actions
- Accidental actions (EN 1991-1-7: 2006). Brussels, Belgium: ECS.
Eads L, Miranda E, Krawinkler H,
et al. (2013) An efficient method for estimating the collapse risk of structures
in seismic regions. Earthquake Engineering & Structural Dynamics
42(1): 25-41.
Ellingwood BR and Dusenberry DO
(2005) Building design for abnormal loads and progressive collapse. Computer-Aided
Civil and Infrastructure Engineering 20(3): 194-205.
Ellingwood BR (2006) Mitigating
risk from abnormal loads and progressive collapse. Journal of Performance
of Constructed Facilities: ASCE 20(4): 315-323.
Elkoly S and El-Ariss B (2014) Progressive
collapse evaluation of externally mitigated reinforced concrete beams. Engineering
Failure Analysis, 40: 33-47.
Fang ZX and Li HQ (2007) Structural
robustness and risk mitigation. Engineering Mechanics 24(S1): 79-82
(in Chinese).
Fascetti A, Kunnath SK and Nisticò
N (2015) Robustness evaluation of RC frame buildings to progressive collapse.
Engineering Structures 86: 242-249.
Fu F (2009) Progressive collapse
analysis of high-rise building with 3-D finite element modeling method. Journal
of Constructional Steel Research 65(6): 1269-1278.
Gardner NJ, Huh J and Chung L (2002)
Lessons from the Sampoong Department Store collapse. Cement & Concrete
Composites 24(6): 523-529.
General Services Administration
(GSA) (2003) Progressive Collapse Analysis and Design Guidelines for New
Federal Office Buildings and Major Modernization Projects. Washington,
DC: GSA.
Hu XB (2007). Studies on the
progressive collapse resistant behavior of the new type polyhedral space frame,
PhD Thesis, Tsinghua University, Beijing, China.
International Standard Organization
(ISO) (2007) Petroleum and Natural Gas Industries-fixed Steel Offshore
Structures (ISO 19902). Geneva, Switzerland: ISO.
Izzuddin BA, Vlassis AG, Elghazouli
AY, et al. (2008) Progressive collapse of multi-storey buildings due to sudden
column loss-part I: simplified assessment framework. Engineering Structures
30(5): 1308-1318.
JalaliLarijani R, Celikag M, Aghayan
I, et al. (2013) Progressive collapse analysis of two existing steel buildings
using a linear static procedure. Structural Engineering and Mechanics
48(2): 207-220.
Khandelwal K and El-Tawil S (2008) Assessment of progressive
collapse residual capacity using pushdown analysis. In: Proceedings of the 2008 Structures Congress, Vancouver, British Columbia, Canada, 24-26 April. pp 1-8.
Reston, VA: ASCE.
Kim T, Kim J and Park J (2009) Investigation
of progressive collapse-resisting capability of steel moment frames using
push-down analysis. Journal of Performance of Constructed Facilities:ASCE
23(5): 327-335.
Kwasniewski L (2010) Nonlinear dynamic
simulations of progressive collapse for a multistory building. Engineering
Structures 32(5): 1223-1235.
Li H and El-Tawil S (2014) Three-dimensional
effects and collapse resistance mechanisms in steel frame buildings. Journal
of Structural Engineering:ASCE 140(SUPPL. 1): A4014017.
Lind NC (1995) A measure of vulnerability
and damage tolerance. Reliability Engineering & System Safety 48(1):
1-6.
Li
Y, Lu XZ, Guan H, et al. (2011) An improved tie force method for progressive
collapse resistance design of reinforced concrete frame structures. Engineering
Structures 33(10): 2931-2942.
Li
Y, Lu XZ, Guan H, et al. (2014a) Progressive collapse resistance demand of
RC frames under catenary mechanism. ACI Structural Journal 111(5):
1225-1234.
Li
Y, Lu XZ, Guan H, et al. (2014b) An energy-based assessment on dynamic amplification
factor for linear static analysis in progressive collapse design of ductile
RC frame structures. Advances in Structural Engineering 17(8): 1217-1225.
Li
Y, Lu XZ, Guan H, et al. (2016) Numerical investigation of progressive collapse
resistance of RC frames subject to column removals from different stories.
Advances in Structural Engineering 19(2): 314-326.
Lu
X, Lu XZ, Guan H, et al. (2013) Collapse simulation of reinforced concrete
high-rise building induced by extreme earthquakes. Earthquake Engineering
& Structural Dynamics 42(5): 705-723.
The Ministry of Housing and Urban-Rural
Development of the People’s Republic of China (MOHURD) (2010a) Code for
Design of Concrete Structures (GB50010-2010). Beijing, China: MOHURD.
The Ministry of Housing and Urban-Rural
Development of the People’s Republic of China (MOHURD) (2010b) Code for Seismic
Design of Buildings (GB50011-2010). Beijing, China: MOHURD.
Murray JA and Sasani M (2013) Seismic
shear-axial failure of reinforced concrete columns vs. system level structural
collapse. Engineering Failure Analysis 32: 382-401.
Nafday AM (2008) System safety performance
metrics for skeletal structures. Journal of Structural Engineering:ASCE
134(3): 499-504.
Qian K and Li B (2012) Slab effects
on the response of reinforced concrete substructures after the loss of a corner
column. ACI Structural Journal 109(6): 845-855.
Ren PQ, Li Y, Zhou YL, et al. (2014)
Experimental study on the progressive collapse resistance of RC slabs. In:
Proceedings of the 2014 Structures Congress, Boston,
MA, 3-5 April, pp. 868-879. Reston, VA: ASCE.
Ren PQ, Li Y, Guan H, et al. (2015)
Progressive collapse resistance of two typical high-rise RC frame shear wall
structures. Journal of Performance of Constructed Facilities: ASCE
29(3): 4014087.
Ruth P, Marchand SM and Williamson
EB (2006) Static equivalency in progressive collapse alternate path analysis:
reducing conservatism while retaining structural integrity. Journal of
Performance of Constructed Facilities:ASCE 20(4): 349-364.
Sadek F, Main JA, Lew HS, et al.
(2011) Testing and analysis of steel and concrete beam-column assemblies under
a column removal scenario. Journal of Structural Engineering:ASCE 137(9):
881-892.
Sasani M (2008) Response of a reinforced
concrete infilled-frame structure to removal of two adjacent columns. Engineering
Structures 30(9): 2478-2491.
Sasani M, Werner A and Kazemi A
(2011) Bar fracture modeling in progressive collapse analysis of reinforced
concrete structures. Engineering Structures 33(2): 401-409.
Shah A (1984). Behavior of L-shaped
reinforced concrete columns under combined biaxial bending and compression.
Master Thesis, New Jersey Institute of Technology, Newark, NJ.
Starossek U and Haberland M (2011)
Approaches to measures of structural robustness. Structure and Infrastructure
Engineering. 7(4): 625-631.
Sun LZ (2006) Experimental research
of RC special-shaped columns under axial force. PhD Thesis, Tianjin University,
Tianjin, China.
Szyniszewskia S and Krauthammer
T (2012) Energy flow in progressive collapse of steel framed buildings. Engineering
Structures 42(9): 1308-1318.
Sørensen JD (2011) Framework
for robustness assessment of timber structures. Engineering Structures
33(11): 3087-3092.
Vamvatsikos D and Cornell CA (2002)
Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics
31(3): 491-514.
Xu G and Ellingwood BR (2011) An
energy-based partial pushdown analysis procedure for assessment of disproportionate
collapse potential. Journal of Constructional Steel Research 67(3):
547-555.
Yi WJ, He QF, Xiao Y, et al. (2008)
Experimental study on progressive collapse-resistant behavior of reinforced
concrete frame structures. ACI Structural Journal 105(4): 433-439.
Zareian F and Krawinkler H (2007)
Assessment of probability of collapse and design for collapse safety. Earthquake
Engineering & Structural Dynamics 36(13): 1901-1914.
Zhang LM and Liu XL (2007) Network of energy transfer in frame structures
and its preliminary application. China Civil Engineering Journal 40(3):
45-49. (in Chinese).
List of Tables and Figures:
Table 1 Structural parameters
of the RC frames
Table 2 Design loads and seismic
action on the RC frames
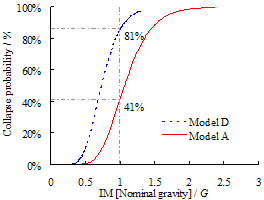
Table 3 Comparison of steel amount
in the beams of Model A and Model D
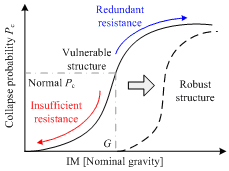
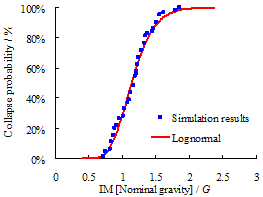
Figure 1 Progressive collapse fragility
curve
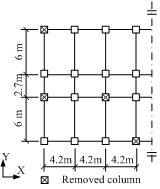
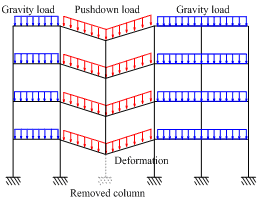
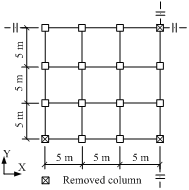
Figure 2 An 8-story RC frame
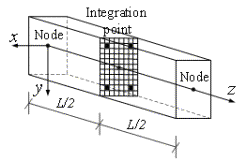
Figure 3 Numerical model of the example
structures
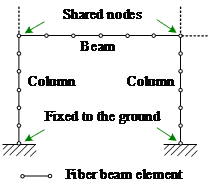
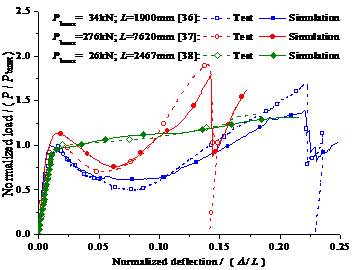
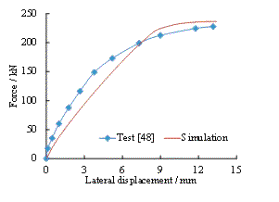
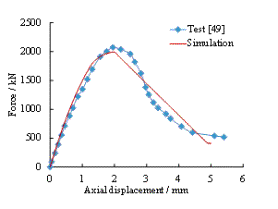
Figure 4 Validation of the fiber beam
model to simulate the progressive collapse tests
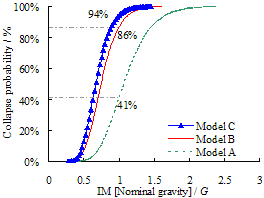
Figure 5 Progressive collapse fragility
curve of Model A
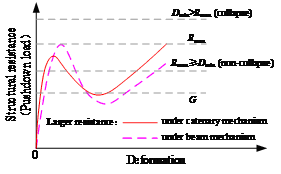
Figure 6 Collapse resistance assessment
via pushdown analysis
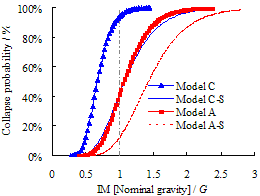
Figure 7 Progressive collapse fragility
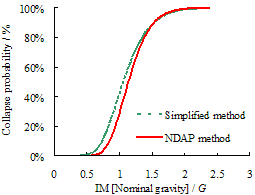
curves based on the simulation results of different methods (Model A)
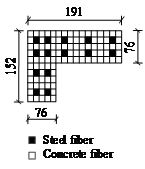
Figure 8 Validation of L-shaped fiber
beam model
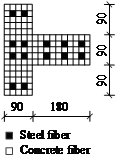
Figure 9 Validation of T-shaped fiber
beam model
Figure 10 4-story RC frame (Model D)
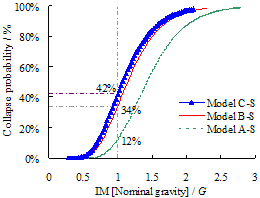
Figure 11 Progressive collapse fragility curves
for frames with different seismic designs
Figure 12 Progressive collapse fragility curves
for frames with and without consideration of slab contributions
Figure 13 Progressive collapse fragility curves
for frames with different layouts
|
![]() Probability-based
progressive collapse-resistant assessment for reinforced concrete frame structures
Probability-based
progressive collapse-resistant assessment for reinforced concrete frame structures