|
5.
Suggestions
for future seismic design
Evaluation of structural
safety against earthquake-induced collapse should consider both collapse fragility
analysis and seismic hazard analysis results, which represent the collapse
resistant capacity of a structure and the earthquake ground motion demand,
respectively. The total collapse probability of a building during its design
service life is proposed as the index to evaluate the earthquake collapse
risk. The process for assessing the total probability of collapse is described
and demonstrated in this paper. With the current Chinese seismic design code,
the collapse risk differs greatly from site to site due to variation in the
seismic hazard. The full range of seismic hazards, especially including mega-earthquakes,
should be considered in seismic design.
The United States
has already begun to consider the influence of actual seismic hazards on collapse
safety in the updated version of its seismic design code. Luco et al. [7]
proposed to modify the uniform-hazard
portions of the seismic design maps in accordance with NEHRP (National Earthquake
Hazards Reduction Program) Provisions to achieve a uniform estimated collapse
probability. The experience of the United States in this regard is a helpful
model for improvement of the Chinese seismic design method.
The objective of uniform-risk-targeted
seismic design for collapse safety of building structures is to ensure that
building structures have the same collapse risk over a prescribed
period no matter where they are located. The collapse risk should be acceptable
by the society and the economy. Because the collapse risk evaluation method
proposed in this paper is not sufficiently developed for current use in seismic
design practice, the following research strategy for developing and implementing
uniform-risk-targeted seismic design for collapse safety is recommended.
(a) Seismic design
zonation is mapped directly according to the collapse-prevention-level earthquake
(e.g., 2% exceedance probability in 50 years), which is based on the
results of seismic hazard analysis.
Ground motion values corresponding to the collapse-prevention-level earthquake
should be used for seismic design. Because the collapse
risk is mainly dominated by the exceedance probability of mega-earthquakes
(defined as earthquakes beyond the collapse-prevention-level),
regions with similar collapse-prevention-level earthquakes should be
further subdivided according to the hazard of mega-earthquakes (which can
also be referred to as a seismic hazard classification).
(b) The relationship
between ground motion values of collapse-prevention-level earthquakes and
the corresponding structural load that is used in seismic design should be
studied to enable the development of a seismic design for reliably ensuring
the collapse safety of buildings subjected to collapse-prevention-level earthquakes.
In other words, the design seismic load should be determined based on the
collapse-prevention-level earthquake zonation map.
(c)
The China¡¯s current seismic design
method as well as earthquake-resistant construction measures should be further
quantitatively evaluated and improved via collapse fragility analysis according
to the seismic hazard classification and seismic design load described in
the previous two steps, until the uniform collapse
probability is achieved.
6.
Conclusions
The concept and the
assessment process for uniform-risk-targeted seismic design are presented
in this paper. The collapse risks of example buildings located in different
regions with the same fortification level but different seismic hazards
are analyzed. The results show that with China¡¯s current seismic design method,
the risk of collapse during a building¡¯s design service life may differ greatly
among different regions. Additional research is required to develop the uniform-risk-targeted
seismic design approach proposed in this paper.
Acknowledgement
This work was supported by the National Natural Science Foundation of
China (Grant Nos. 90815025, 51178249), the Tsinghua University Research
Funds (Grant Nos. 2010THZ02-1, 2010Z01001) and the Program for New Century
Excellent Talents in University (Grant No. NCET-10-0528).
Appendix
The following derivation
is provided to prove the equivalence of the
following equations.
| |
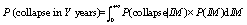
|
(1)
|
| |
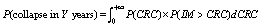
|
(2)
|
|
|
|
|
To facilitate the mathematical
expressions of Equations (1) and (2), the probabilistic functions are expressed as
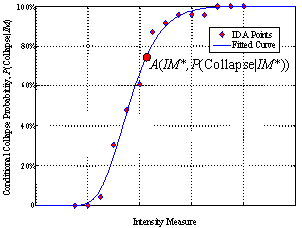
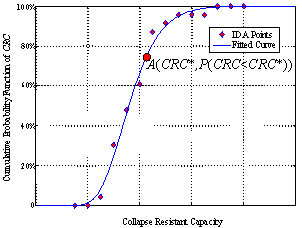
P(collapse|IM)=F(x)
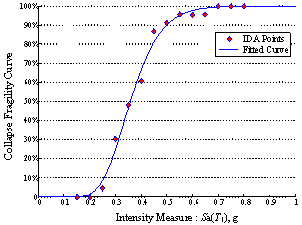
is the conditional collapse probability at given values of the intensity level,
which equals the cumulative distribution function of CRC as discussed
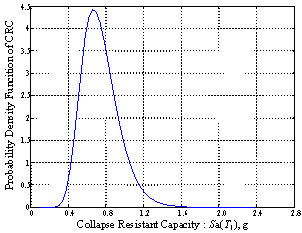
in the paper. P(CRC)=f(x) can be treated as the
probability that the structure¡¯s collapse resistant capacity equals CRC,
which is also the probability density function of CRC. Therefore, F(x)
and f(x) should satisfy the following equation.
| |
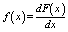
|
(11)
|
P(IM)=g(x)
is the probability density function that the building site experiences
earthquakes of intensities equal to IM
during the design service life. P(IM>CRC)=G(x)
is the likelihood that the building site experiences earthquakes with
intensities larger than CRC during the design service life.
Thus, g(x) and G(x)
satisfy the following equation.
| |
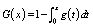
|
(12)
|
After integrating Equation (1) by parts and
inserting Equation (12)
into it, the following equation is obtained.
For 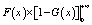 in Equation
(13),
when x=+¡Þ, F(x)=P(collapse|IM)
can be regarded as the conditional collapse probability when a building is
subjected to an earthquake with IM=+¡Þ and thus it equals one. G(x)=P(IM>CRC)
is the likelihood that the building site experiences earthquakes with
IM greater than +¡Þ and thus G(x)=P(IM>CRC)
equals zero. Similarly, when x=0,
F(x)=P(collapse|IM) can
be regarded as the conditional collapse probability when a building is subjected
to an earthquake with IM=0 and thus F(x)=P(collapse|IM) equals zero.
G(x)=P(IM>CRC) is the
likelihood that the building site experiences earthquakes with IM larger
than 0 and thus equals one. Therefore,
in Equation
(13),
when x=+¡Þ, F(x)=P(collapse|IM)
can be regarded as the conditional collapse probability when a building is
subjected to an earthquake with IM=+¡Þ and thus it equals one. G(x)=P(IM>CRC)
is the likelihood that the building site experiences earthquakes with
IM greater than +¡Þ and thus G(x)=P(IM>CRC)
equals zero. Similarly, when x=0,
F(x)=P(collapse|IM) can
be regarded as the conditional collapse probability when a building is subjected
to an earthquake with IM=0 and thus F(x)=P(collapse|IM) equals zero.
G(x)=P(IM>CRC) is the
likelihood that the building site experiences earthquakes with IM larger
than 0 and thus equals one. Therefore,
| |
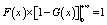
|
(14)
|
Substituting Equations
(11)
and (14)
into Equation (13) leads to the
following equation.
Because f(x)=P(CRC)
denotes the probability density function of the collapse resistant capacity,
| |

|
(16)
|
Substituting Equation
(16) into Equation (15) yields
The equivalence of
Equation (1)
and Equation (2) has been proven.
References
[1]
Ye L P, Qu Z, Lu X Z, Feng P.
Collapse prevention of building structures: a lesson from the Wenchuan
earthquake. Journal of Building Structures, 2008, 29(4): 42-50. (in Chinese)
[2]
Ye L P, Lu X Z, Li Y. Design
objectives and collapse prevention for building structures in mega-earthquake.
Earthquake Engineering and Engineering Vibration, 2010, 9(2): 189-200.
[3]
Lu X Z, Ye L P. Study on the
seismic collapse resistance of structural system. Earthquake Resistant
Engineering and Retrofitting, 2010, 32(1): 13-18. (in Chinese)
[4]
Zareian F, Krawinkler H. Assessment
of probability of collapse and design for collapse safety. Earthquake Engineering
and Structural
Dynamics, 2007, 36(13):
1901¨C1914.
[5]
Shi W, Ye L P, Lu X Z, Tang D
Y. Study on the collapse-resistant capacity of RC frames with different
seismic fortification levels. Engineering Mechanics, 2010, 28(3): 41-48.
(in Chinese)
[6]
Vamvatsikos D, Cornell C A. Incremental
dynamic analysis. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514.
[7]
Nicolas L, Ellingwood B R, Ronald O H, etc. Risk-targeted versus
current seismic design maps for the conterminous United States. SEAOC 2007
Convention Proceedings.
[8]
Li Y, Yin Y J, Ellingwood B R,
Willian M B. Uniform hazard versus uniform risk bases for performance-based
earthquake engineering of light-frame wood construction. Earthquake Engineering
and Structural Dynamics, 2010, 39(11): 1199-1217.
[9]
GB 50011-2010, Code for seismic
design of buildings. 2010. (in Chinese)
[10] Gao M T, Lu S D. The Discussion on principles of seismic zonation
of the next generation. Technology for Earthquake Disaster Prevention, 2006,
1(1): 1-6. (in Chinese)
[11] FEMA 695. Quantification of building
seismic performance factors. California, 2009.
[12] Ge Y B. Probability Theorem and
mathematical statistics. Beijing, Tsinghua University Press, 2005. (in Chinese)
[13] McGuire
R K. Probabilistic
seismic hazard analysis and design earthquakes: closing the loop. Bulletin
of the Seismological Society of America, 1995, 85(5): 1275-1284.
[14] Lu X
Z, Lin X
C, Ma Y
H, Li Y,
Ye L P.
Numerical simulation for the progressive collapse of concrete building
due to earthquake, Proc. the 14th World Conference on Earthquake Engineering,
October 12-17, 2008, Beijing, China, CDROM.
[15] Lu X Z, Ye L P, Miao Z W. Elasto-plastic
analysis of building against earthquake. Beijing, China Building
Industry Press, 2009. (in Chinese)
[16] Li Y, Lu X Z, Guan H, Ye L P.
An improved tie force method for progressive collapse resistance design
of reinforced concrete frame structures. Engineering Structures, 2011,
33(10): 2931-2942.
[17] Lu X, Lu X Z, Zhang W K, Ye L
P. Collapse simulation of a super high-rise building subjected to extremely
strong earthquakes. Science China Technological Sciences, 2011, 54(10):
2549-2560.
[18] Miao Z W, Ye L P, Guan H, Lu
X Z. Evaluation of modal and traditional pushover analyses in frame-shear-wall
structures. Advances in Structural Engineering, 2011, 14(5): 815-836.
[19] Tang B X, Lu X Z, Ye L P, Shi
W. Evaluation of collapse resistance of RC frame structures for Chinese
schools in seismic design categories B and C. Earthquake Engineering and
Engineering Vibration, 2011, 10(3): 369-377.
[20]
CECS 160:2004. General
rule for performance-based seismic design for buildings. 2001. (in Chinese)
|
![]()
![]()
![]()
![]()