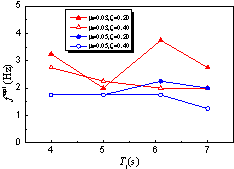
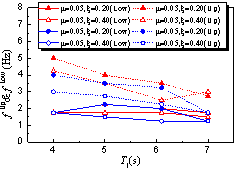
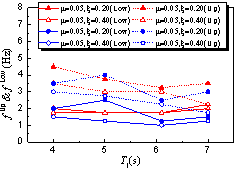
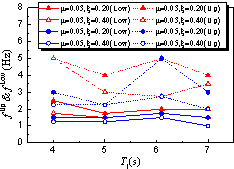
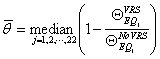|
References
Aly AM. 2014. Proposed robust tuned mass damper for response mitigation in
buildings exposed to multidirectional wind. Structural Design of Tall
and Special Buildings 23(9): 664-691.
DOI: 10.1002/tal.1068
Angelis MD, Perno S, Reggio A. 2012.
Dynamic response and optimal design of structures with large mass ratio TMD.
Earthquake Engineering & Structural Dynamics 41(1): 41-60.
DOI: 10.1002/eqe.1117.
Bakre SV, Jangid RS. 2007. Optimum
parameters of tuned mass damper for damped main system. Structural
Control & Health Monitoring 14(3): 448-470. DOI: 10.1002/stc.166.
Bekdaş G, Nigdeli SM. 2011. Estimating
optimum parameters of tuned mass dampers using harmony search. Engineering
Structures 33(9): 2716–2723. DOI: 10.1016/j.engstruct.2011.05.024.
Bu D, Guo W. 2014. Structural design of super high-rise
building of Greenland Central Office Building. Building
Structure 44(S2): 24-28. (in Chinese)
Chai W, Feng MQ. 1997. Vibration control of super tall buildings subjected to wind
loads. International Journal of Non-Linear Mechanics 32(4):
657–668. DOI: 10.1016/S0020-7462(96)00094-7.
Chen CP, Zhang HY, Lou DH. 2012. Structural design on a super high-rise office
building in Hangzhou. Building
Structure 42(S2): 241-245. (in Chinese)
Chen QJ, Yuan WZ, Li YC, Chao LY. 2013a. Dynamic
response characteristics of super high-rise buildings subjected to long-period
ground motions. Journal of Central South University 20(5): 1341-1353. DOI: 10.1007/s11771-013-1621-9.
Chen Y, Chen ZZ, Lu JF. 2013b. Structural
scheme selection and performance-based seismic design of Chang’anwanke Center.
Building Structure 43(S1): 21-27. (in Chinese)
Cheung YL, Wong WO. 2011. H-infinity
optimization of a variant design of the dynamic vibration absorber—Revisited
and new results. Journal of Sound & Vibration 330(16):
3901-3912. DOI: 10.1016/j.jsv.2011.03.027.
Chulahwat A. 2015. Hybrid tuned mass damper and isolation
floor slab system optimized for vibration control. Journal of Earthquake
Engineering 19(8): 1197-1221. DOI: 10.1080/13632469.2015.1037406.
FEMA. 2009. Quantification of building seismic performance factors, FEMA-P695.
Federal Emergency Management Agency: Washington, DC.
FEMA. 2012. Seismic performance assessment of buildings volume 1-methodology,
FEMA-P58. Federal Emergency Management Agency: Washington, DC.
Feng K, Wen LY, Zhang XP, Li MY, Han HJ, Liu BW, Che ZX. 2015. Mixed structural scheme analysis and design of main
tower building of Haikou Center. Building Structure 45(4): 41-46. (in Chinese)
Feng MQ, Mita A. 1995. Vibration
control of tall building using mega subconfiguration. Journal of Engineering
Mechanics 121(10): 1082-1088. DOI: 10.1061/(ASCE)0733-9399(1995)121:10(1082).
Fu XY, Wu B, Chen XC, Meng ML, Sun C, Jiang H.B, Gao Y, Li JW. 2008. Summarization
of research on the structural design of a super high-rise building in Qatar. Journal of Building Structures 29(1): 1-8. (in Chinese)
Gong L, Zhang TL. 2011. The structural design plan of Tianjin “345” high-rise office tower. Construction & Design for Project 2011(11): 51-55. (in Chinese)
Greco R, Lucchini A, Marano GC. 2015. Robust design of tuned mass dampers installed
on multi-degree-of-freedom structures subjected to seismic action. Engineering
Optimization 47(8): 1009-1030. DOI: 10.1080/0305215X.2014.941288
Guo QQ. 2005. The structural setting and optimization of super high-rise building.
Tongji University; 6-10.
(in Chinese)
Ha MQ, Li W, Lu CY, Li XT, Shi L, Pan HH, Wang ZK, Ding Y, Li X, Luo PH, Li
XW. 2015a Structural design on super high-rise building
of Ningbo Greenland Center. Building
Structure 45(07):
17-24. (in Chinese)
Ha MQ, Li W, Pan HH, Lu CY, Li XT, Shi L, Wang ZK, Ding Y, Li R. 2015b. Super
high-rise structural design of Taizhou China Resources Center. Building
Structure 45(8): 1-7. (in Chinese)
Han YD, Wang LW, Long HY, Zhu J. 2013. Structural design of super-high building for China Railway Xi'an Center.
Building Structure 43(23): 42-46. (in Chinese)
Hartog D, Pieter J.
1956. Mechanical vibrations. New York:
McGraw-Hill; 492.
Hoang N, Fujino Y, Warnitchai P. 2008.
Optimal tuned mass damper for seismic applications and practical design formulas.
Engineering Structures 30(3): 707–715. DOI: 10.1016/j.engstruct.2007.05.007.
Huang ZH, Liao Y, Wang LY, Chao CH, Li ZS. 2011. Elastic-plastic time-history
analysis of PINGAN IFG under rare earthquakes. Building Structure 41(S1): 40-44. (in Chinese)
Jiang Q, Lu XZ, Guan
H, Ye XG. 2014. Shaking table model test and FE analysis of a reinforced concrete
mega-frame structure with tuned mass dampers.
Structural Design of Tall and Special Buildings 23(18): 1426–1442.
DOI: 10.1002/tal.1150.
Krenk S, Høgsberg J. 2008. Tuned
mass absorbers on damped structures under random load. Probabilistic
Engineering Mechanics 23 (4): 408-415. DOI: 10.1016/j.probengmech.2007.04.004.
Landi L, Fabbri O, Diotallevi PP.
2014. A two-step direct method for estimating the seismic
response of nonlinear structures equipped with nonlinear viscous dampers.
Earthquake Engineering & Structural Dynamics 43(11): 1641-1659.
DOI: 10.1002/eqe.2415.
Lan ZJ, Tian YJ, Fang L, Liang ST, Wang XD. 2004. An experimental study on seismic responses
of multifunctional vibration-absorption reinforced
concrete megaframe structures. Earthquake Engineering & Structural
Dynamics 33(1): 1-14. DOI: 10.1002/epe.324.
Lan ZJ, Wang XD, Dai H, Liang ST. 2000. Multifunctional vibration–absorption RC megaframe structures
and their seismic responses. Earthquake Engineering & Structural
Dynamics 29(8): 1239–1248. DOI:
10.1002/1096-9845(200008)29:8<1239::AID-EQE956>3.0.CO;2-1.
Limazie T, Zhang XA, Wang XJ. 2013. Vibration control parameters investigation of the Mega-Sub
Controlled Structure System (MSCSS). Earthquakes & Structures 5(2):
225-237. DOI: 10.12989/eas.2013.5.2.225.
Li N, Zhen QH, Zhao T. 2013. Structural design of Guangzhou Greenland
Financial Center super high-rise building. Building
Structure 43(S1): 14-20. (in Chinese)
Liu MY, Chiang WL, Hwang JH, Chu CR. 2008. Wind-induced vibration of high-rise
building with tuned mass damper including soil–structure interaction.
Journal of Wind Engineering and Industrial Aerodynamics 96 (6):
1092-1102. DOI: 10.1016/j.jweia.2007.06.034.
Liu P, Yin C, Li XY, Liu GL, Huang XY, He WM, Li ZQ. 2012. Structural system
design and study of Tianjin Goldin 117
Mega Tower.
Building Structure 42(3): 1-9. (in Chinese)
Liu QX, Zhang JJ, Wang QW, Wei GW, Luo RW, Wang YS, Zhou B, Yang WH. 2014. Structural
design of super high-rise building of Kashi
International Plaza. Proceedings of the Symposium China Construction Metal Structure
Association Steel Structure Association annual meeting and Steel Construction
Expert Committee: 28-35. (in Chinese)
Lu
X, Lu XZ, Guan H, Ye LP. 2013a. Comparison and selection
of ground motion intensity measures for seismic design of super high-rise
buildings. Advances
in Structural Engineering 16(7): 1249-1262.
Lu X,
Lu XZ, Sezen H, Ye LP. 2014. Development of a simplified model and seismic energy dissipation
in a super-tall building.
Engineering Structures 67(4): 109-122. DOI: 10.1016/j.engstruct.2014.02.017.
Lu
X, Lu XZ, Zhang WK, Ye LP. 2011. Collapse simulation of a super high-rise
building subjected to extremely strong earthquakes. Science China Technological
Sciences 54(10): 2549-2560. DOI: 10.1007/s11431-011-4548-0.
Lu XZ, Li MK, Guan H,
Lu X, Ye LP. 2015. A comparative case study on seismic design of tall RC
frame-core tube structures in China and USA. Structural Design of Tall and Special
Buildings 24(9): 687-702. DOI: 10.1002/tal.1206.
Lu XZ, Lu X,
Guan H, Zhang WK, Ye LP. 2013b. Earthquake-induced collapse simulation of a super-tall
mega-braced frame-core tube building.
Journal of Constructional Steel Research 82(3):
59-71. DOI: 10.1016/j.jcsr.2012.12.004.
Lu XZ, Xie LL, Yu
C, Lu X. 2016. Development
and application of a simplified model for the design of a super-tall mega-braced
frame-core tube building. Engineering Structures 110(3):
116-126. DOI: 10.1016/j.engstruct.2015.11.039.
Marano GC, Greco R, Trentadue F, Chiaia B. 2007. Constrained reliability-based optimization of linear tuned mass
dampers for seismic control. International Journal of Solids &
Structures 44(22): 7370-7388. DOI: 10.1016/j.ijsolstr.2007.04.012.
Miranda E, Taghavi S. 2005. Approximate floor acceleration demands in multistory buildings.
I: Formulation. Journal of Structural Engineering 131(2):
203-211. DOI: 10.1061/(ASCE)0733-9445(2005)131:2(203).
MOHURD. 2009. National Technical Measures
for Design of Civil Construction: Structure. Ministry of Housing and Urban-Rural
Development of the People’s Republic of China. China Planning Press: Beijing,
China. (in Chinese)
MOHURD, 2010. Code
for seismic design of buildings (GB50011-2010). Ministry of Housing and Urban-Rural Development
of the People’s Republic of China. China Architecture & Building Press: Beijing, China
(in Chinese).
Ozsariyildiz SS, Bozer A. 2015. Finding
optimal parameters of tuned mass dampers. Structural Design of Tall
and Special Buildings 24(6): 461-475. DOI: 10.1002/tal.1174.
PEER. 2010. Guidelines for performance-based seismic design of tall buildings.
Berkeley: University of California (PEER Report No. 2010/05).
Piedrafita D, Cahis X, Simon E, Comas J. 2015. A new perforated core buckling restrained
brace. Engineering Structures 85(2): 118-126. DOI:
10.1016/j.engstruct.2014.12.020.
Qi JW, Hao GQ, Du YS, Liu LN, Zhang LC, Li RQ. 2010. Structural design of super high-rise building of Hebei Kaiyuan World Center.
Building Structure
40(12): 74-79. (in Chinese)
Qiu K, Rao GX, Cai J, Wei L. 2013. Structural design of Shenzhen NEO Building.
Building Structure
43(S1): 28-32. (in Chinese)
Rüdinger F. 2014. Optimal
vibration absorber with nonlinear viscous power law damping and white noise
excitation. Journal of Engineering Mechanics 132(1): 46-53.
DOI: 10.1061/(ASCE)0733-9399(2006)132:1(46).
Sadek F, Mohraz B, Taylor AW, Chung RM. 1997. A method of estimating the parameters
of tuned mass dampers for seismic applications. Earthquake Engineering
& Structural Dynamics 26(6): 617-635. DOI: 10.1002/(SICI)1096-9845(199706)26:6<617::AID-EQE664>3.0.CO;2-Z.
Shome N, Jayaram N, Krawinkler H, Rahnama M. 2013. Loss
estimation of tall buildings designed for the PEER tall building initiative
project. Earthquake Spectra 31(3): 1309-1336. DOI:
10.1193/121912EQS352M.
Sun HL, Chen JM, Feng ZQ. 2013. Structural
design of out-of-code super high-rise building of Yunfu Mansion in Wuxi. Building
Structure 43(18): 1-7. (in Chinese)
Tan P, Li XX, Liu LK, Zhang Y. 2014. Control mechanism and performance analysis of a mega-sub
structure control system. China Civil Engineering Journal 47(11): 55-63.
(in Chinese)
Tian Y, Lu X, Lu XZ, Li MK, Guan H. 2016.
Quantifying the seismic resilience of two tall buildings designed using Chinese
and US codes. Earthquakes and Structures, in press.
Vafaei D, Eskandari R. 2015. Seismic
response of mega buckling-restrained braces subjected to fling-step and forward-directivity
near-fault ground motions. Structural Design of Tall and Special Buildings 24(9): 672–686. DOI:
10.1002/tal.1205.
Wang CL, Li FL, Zhu WP, Li Y, Liu ZC, Shang CY. 2004. Structural design on Dalian
Guomao Tower. Proceedings
of the 18th National Symposium of High-rise Building Structure: 468-479. (in Chinese)
Wang
CL, Lu ZT, Wu J. 2008. Analysis of the
mechanism and efficiency of vibration-absorption for semi-flexible suspension
systems.
China Civil Engineering
Journal 41(1): 48-54. (in Chinese)
Wang LC, Wang XJ, Ji DH, Qu XF, Liu N, Zuo QL, Li DF, Wen HL, Guan J, Cao L.
2012. Structural design and analysis on Dalian Guomao Tower. Building
Structure 42(2): 74-80. (in Chinese)
Wang J. 2012. Structural design of Changzhou Runhua World
Center. Building Structure
42(5): 87-91. (in Chinese)
Wang WF, Wu K, Che SL. 2014. Structural design on a block super high-rise building
of Xi'an Greenland Center. Building Structure 44(15): 1-6. (in Chinese)
Wang W, Zhao XD. 2014. Research
on key problems in the design of the super high-rise building of Xiamen International
Center. Building Structure
44(14): 44-49. (in Chinese)
Wu SH, Sun F, Zou AY, Yan KS, Wan YX, Chen Y, Zhang LH, Wu LJ, Yu YL. 2013.
Structural design on super tall buildings of Tianjin R&F Center. Building
Structure 41(11): 42-50. (in Chinese)
Xiang P, Nishitani A. 2015. Optimum design and application of non‐traditional tuned
mass damper toward seismic response control with experimental test verification. Earthquake Engineering & Structural
Dynamics 44(13): 2199–2220. DOI: 10.1002/eqe.2579.
Xu PF, Xiao CZ, Li JH. 2014. Study
on relationship between natural vibration periods and heights of structures
for high-rise buildings and its reference range.
China Civil Engineering
Journal 47(2):
1-11. (in Chinese)
Xu YJ, Wang RC, Yu SY, Li KN, Hong L. 2002. Structural design and safety analysis
of Shanxi Information Tower. Journal
of Building Structures
23(1): 89-95. (in Chinese)
Yan F, Zhou JL, Wang DS, Zheng L, Lang T. 2007. Structural design of Nanjing
Greenland Zifeng Mansion super high-rise building. Building Structure 37(5): 20-24. (in Chinese)
Yang XM, Xu HC, Zheng W, Bao LJ. 2013. Structural seismic design of Luoyang Zhengda ultra-limit high-rise office building.
Building Structure 43(18): 39-43. (in Chinese)
Yu JH, Li LC, Ding YJ, Zhang XZ. 2015. Structural
design of super high-rise building of Tianjin Junlin Building. Building Structure 45(1): 1-4. (in Chinese)
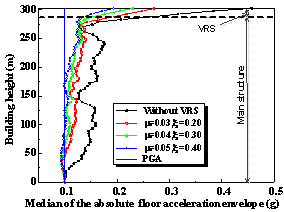
Zhang L, Jiang Q, Lu XZ, Ye LP. 2015.
Analysis on the control effect of TMD on the seismic story acceleration of
super high-rise buildings. Earthquake Engineering & Engineering Dynamics 35(10):
84-89. (in Chinese)
Zhang XA, Qin XJ, Cherry S, Lian YD, Zhang JL, Jiang JS. 2009. A
new proposed passive mega-sub controlled structure and response control.
Journal of Earthquake Engineering 13(2): 252-274. DOI: 10.1080/13632460802347422.
Zhou X, Lin Y, Gu M. 2015. Optimization of multiple tuned mass dampers for large-span
roof structures subjected to wind loads. Wind & Structures An International
Journal 20(3): 363-388. DOI: 10.12989/was.2015.20.3.363
Zhou YW, Li H. 2006. Structural optimization of a super high-rise building. West China
Exploration Engineering (5): 255-258. (in Chinese)
Zhu H. 2008. The structural design scheme of a super high-rise building. Industrial Construction 38(S1): 433-437. (in Chinese)
Zhu LG, Lu L. 2012. Structural design challenge of super high-rise
tower building of CQ TP2.
Building Structure 42(10): 33-40. (in Chinese)
Zuo L, Nayfeh SA. 2005. Optimization of the individual stiffness and damping
parameters in multiple-tuned-mass-damper systems. Journal of
Vibration and Acoustics 127(1): 77-83. DOI: 10.1115/1.1855929.
Correspondence to: Xinzheng
Lu, Department of Civil Engineering, Key Laboratory of Civil Engineering Safety
and Durability of China Education Ministry, Tsinghua University, Beijing,
P.R. China. E-mail: luxz@tsinghua.edu.cn
|
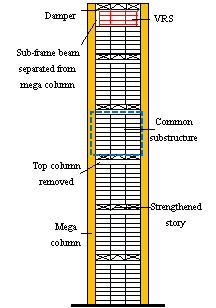

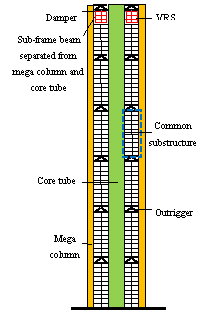

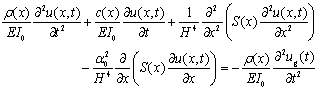
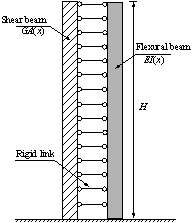
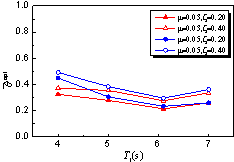
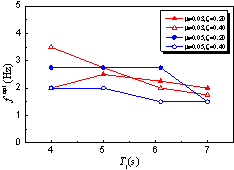
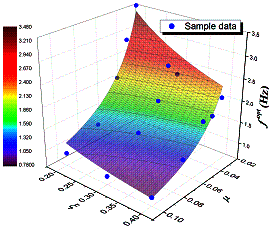
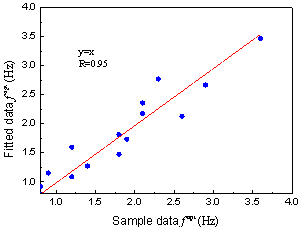
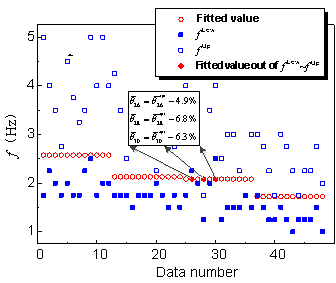
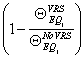 , as presented
in Equation 5.
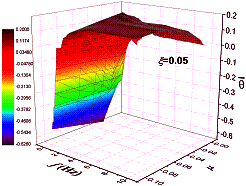
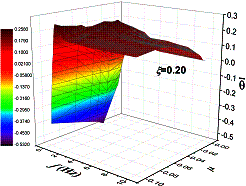
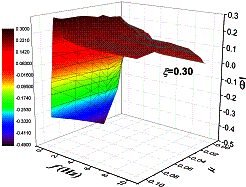
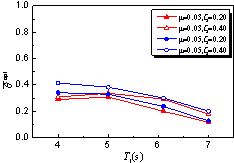
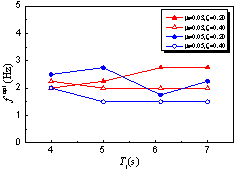
, as presented
in Equation 5.