1 Introduction

The perimeter columns of the ground floor of a RC frame are generally more vulnerable to accidents, which could lead to an initial local failure. Such a failure may spread throughout the entire structure and result in a disproportionate or overall structural failure, defined as the progressive collapse of a building structure [1]. The most typical example of this kind of progressive collapse is the 1995 bombing of the Murrah Federal Building (MFB) in Oklahoma City [2]. The truck bomb completely destroyed an edge column on the ground floor and damaged the adjacent columns, eventually leading to a substantial collapse of MFB. Given that a progressive collapse will result in severe casualties and economic losses, both current design codes [1, 3-4] and specific guidelines [5-6] offer design and strengthening methods in an attempt to improve the progressive collapse resistance of building structures. In these methods, the collapse risk analyses and strengthening techniques have been developed with a primary focus on the collapse scenarios caused by the loss of corner, edge and interior vertical load-bearing components.

With rapid development of experimental and numerical analysis techniques, extensive in-depth studies have been conducted during the last decade investigating the progressive collapse resistance of building structures, including RC frame structures [7-9], frame-shear wall structures [10-11] and flat plate structures [12-16]. Remarkable efforts have been made towards understanding structural collapse patterns [17], collapse-resistant mechanisms [18-19], dynamic effects [20-22], resistance assessment methods [23], fire-induced collapse [24, 25] and developing various collapse-resistant design methods [26-28].

RC frames are one of the most important and commonly used structural systems. For this reason, a large number of experiments have been conducted to investigate the progressive collapse resistance of this kind of structures. Nevertheless, the existing experiments mainly focused on beams [29], plane frames [30] and beam-column substructures [31-33] in which the effects of the slabs on the collapse resistance of the overall frame were neglected. The floor system composed of beams and slabs is the key element of an entire structure to resist progressive collapse, by which the unbalanced gravity load induced by the initial local failure is transferred to the remaining structure Published experiments on beam-slab substructures [34-35] indicate that slabs can significantly improve the progressive collapse resistance of an RC frame. This is because the slab exhibits a compressive membrane action under small deformations and a tensile membrane action under large deformations to provide additional structural resistance. The effect of comprehensive structural parameters on the progressive collapse of one-way RC beam-slab frame substructures under a middle column removal scenario has also been investigated through the experiment [35].

Existing experiments on the progressive collapse of beam-slab substructures have been devoted to the corner column [34, 36] and interior column [18] removal scenarios. Limited work has been done on an edge-column removal scenario. When a RC frame subjected to an edge-column-removal scenario, its floor system exhibits a complicated mechanism against progressive collapse due to the different constraint conditions at the structural boundaries along the two planar directions. Xiao et al. [37] conducted a dynamic collapse test by removing two edge columns of a 1/2 scaled 3-story RC frame and analyzed its dynamic response. Pham and Tan [38] performed an experiment on the progressive collapse resistance of a 1/3 scaled single-story RC frame under the penultimate-external column (near the corner column) removal scenario. Qian et al. [39] tested two 1/4 scaled slab-beam-column substructures subjected to an edge-column and two-column removal scenarios. Despite these research efforts, the entire progressive collapse process is rather complicated, and it is especially challenging to quantify the interactions between the slabs and the frame beams.

In this study, five 1/3 scaled RC frame substructures, including four beam-slab specimens and one beam specimen without a slab, were fabricated. The static loading approach was used to investigate the progressive collapse of the substructure specimens under an edge-column removal scenario. Special efforts were made to (1) analyze the collapse-resistant mechanisms and failure patterns of the specimens with emphasize on the effects of the slabs; (2) analyze the effects of the structural parameters (i.e., beam height, slab thickness and seismic reinforcement) on the collapse resistance.

2 Experimental scheme

2.1 Design of the specimens

The prototype structure is a six-story RC frame designed according to the Chinese Code for the Design of Concrete Structures [40] and the Code for Seismic Design of Buildings [41], as shown in Figure 1. The first story and the remaining stories are 4.2 m and 3.6m in height, respectively. The span in both directions is 6 m. The seismic design intensity is 6 degree, i.e., the peak ground acceleration (PGA) is 0.05 g for the design earthquake (with a 10% probability of exceedance in 50 years), where g is the acceleration of gravity. The design dead and live loads are 5.0 kN/m² and 2.0 kN/m², respectively.

A two-bay beam-slab substructure on the first floor was isolated from the entire structure, which is highlighted with the shaded area enveloped by the red-colored rectangle, as shown in Figure 1b. A 1/3-scaled ratio was adopted in the test due to the space limitation of the laboratory. Similar scale ratios were also adopted in the work of Yi et al. [30] and Qian and Li [12, 34]. The dimensions of the prototype structure and the scaled control specimen SE1 are given in Table 1.

Table 1 Dimensions of the prototype structure and the scaled specimen (unit: mm)

In real situation, the test area (the shaded area in Figure 1b) is restrained by the surrounding slabs and beams. In the experiments, apart from the free edge, the other three perimeter edges of the test substructures were simplified as fixed restraints. Such fixed restraints were achieved by adding three strong boundary beams as shown in Figure 2. Having a much larger cross-section than those of the test beams and slabs, the boundary beams are able to provide ideal fixities at the boundaries (see Figure 3). To avoid potential initial damage of the specimens during transportation and installation, four lifting beams were casted together with the boundary beams. All the gravity loads of the test substructures were carried by the lifting beams during installation. Detailed dimensions of the test substructures are shown in Figure 3. The sectional sizes of the boundary beams in the X- and Y-directions were 400 mm ¡Á 370 mm and 500 mm ¡Á 370 mm, respectively. The dimensions of the lifting beams were 200 mm ¡Á200 mm.

Figure 2 Test area of the substructure (unit: mm)

(a) Plan view

(b) Section I-I

Figure 3 Detailed dimensions of SE1 (unit: mm)

Five specimens (i.e., SE1 to SE4 and BE1) were designed. SE1 was the control beam-slab substructure specimen and BE1 was the beam specimen without a slab. All the design parameters (except for the slab) of SE1 were identical with those of BE1. In order to study the effects of the structural parameters (i.e., beam height, slab thickness and seismic reinforcement) on the progressive collapse resistance, three other beam-slab specimens designated as SE2, SE3 and SE4 were also manufactured. Only one structural parameter of each of the three specimens differed from the control specimen SE1: SE2 had a larger slab thickness of 75mm; SE3 had a greater beam height of 200 mm; SE4 had a higher seismic design intensity of 8 degree, i.e., the PGA was 0.2g for the design earthquake. The scaled specimens had the same reinforcement ratio as that in the prototype structure. The reinforcement arrangement in the beams and slabs of SE1 is shown in Figures 4 and 5. Dimensions and reinforcement details of all the specimens are summarized in Tables 2 and 3. As SE2 had a thicker slab than SE1, its slab reinforcement was increased according to the minimum slab reinforcement specified by the Chinese Code for the Design of Concrete Structures [40]. The beam reinforcement in SE4 was also increased to sustain higher seismic design intensities than that of SE1.

Table 2 Sectional dimensions and beam reinforcements in the specimens (unit: mm)

Table 3 Slab reinforcements in the specimens (unit: mm)

Note: ^a The illustration of the Zones a to d are shown in Figure 5

Figure 4 Reinforcements in the beams of SE1 (unit: mm)

Note: The reinforcement details in Zones a to d are given in Table 3. 

Figure 5 Reinforcements in the slabs of SE1 (unit: mm)

2.2 Test setup and instrumentation

Three large concrete bases fixed on the strong floor were placed under the boundary beams to provide the fixity to the boundary beams and the sufficient space to accommodate large deformations during the test (Figure 6). The displacement and rotation of the boundaries along the south-north (S-N) direction were restrained by the welded and bolted thick steel plates connecting the embedded steel plates in the boundary beams and the concrete bases (Figure 6a). A 500 kN vertical load was applied to Boundary beam 3 (Figure 2) from a hydraulic actuator to guarantee its perfect contact to the base, by which the displacement and rotation of Boundary beam 3 along the west-east (W-E) direction was also restrained (Figure 6b). Three linear variable differential transducers (LVDTs) were installed on the boundary beams to monitor their displacements. The measured maximum displacement of the boundary beams was 0.003 mm, further confirming the fixity of the boundary condition during testing.

Figure 6 Boundary conditions applied in the tests

In order to achieve a displacement-controlled static loading condition, two hydraulic actuators, one above and the other below the specimen, were used to apply a concentrated vertical load to the stub of the removed edge column. At the beginning of each test, a pair of balanced small forces (< 10 kN) were simultaneously applied by the two actuators. Afterwards, a constant force was maintained by the lower actuator and a gradually increased force was applied through the upper actuator. The loading rate was controlled by the displacement of the column stub. A steel hinge joint was designed and installed on the top of the stub (Figure 7) to release the rotation along the X-direction of the stub during large deformations. Note that applying a concentrated load may not accurately reflect a real column loss scenario. However it is considered a feasible loading scheme due to the simplicity in stability control of the applied load. It is also a viable option for the purpose of comparing experimental results between the beam specimen and the beam-slab specimens. The loading process was terminated upon rupture of a large number of longitudinal reinforcement and significant declination of the collapse resistance of the specimens.

Figure 7 One-way hinge on top of the column stub

A series of LVDTs were installed at the four corners of the concrete stub, the mid-span of the X- and Y-beams and the center of the slabs, as shown in Figure 2. Nine typical sections of the substructure were defined as Sections A to I (Figure 2). Strain gauges were placed on the steel bars and concrete at these typical sections to monitor the strain development of the specimens.

2.3 Material properties

HPB 300 rebars were used in the specimens with diameters of 6 mm, 8 mm, 10 mm, and 12 mm, and 4-mm-diameter cold-drawn steel wires were used for stirrups. The material properties of the rebars are given in Table 4. The specimens were casted with C30-grade concrete, with an average compressive cube strength of 43 MPa, which was determined using the standard cubes with a size of 150 mm¡Á150 mm¡Á150 mm.

Table 4 Material properties of the rebars

3 Experimental phenomena

3.1 Beam specimen BE1

The load-displacement curve and the final failure mode of BE1 are shown in Figures 8 and 9, respectively. The load refers to the external load applied to the concrete stub and the displacement is the corresponding vertical displacement of the stub. In the load-displacement curve, six typical points are identified, including the initial point (Point o), the rebar yielding point (Point a), the peak point of the beam mechanism (Point b), the transition point between the beam and the catenary mechanisms (Point c), the peak point of the catenary mechanism (Point d) and the point indicating the maximum vertical displacement (Point e). Specifically, the load and displacement at points b, c and d are defined as (F_b, D_b), (F_t, D_t) and (F_c, D_c), respectively.

Figure 8 Load-displacement curves of BE1 and SE1

(a) The X-beams

(b) The Y-beam

Figure 9 Failure modes of BE1

When the displacement reached 4 mm, 10 mm and 16 mm respectively, flexural cracks along the cross section were observed at the bottom of Sections C and D, the top of Sections A and F and the top of Section G (Figure 9). Afterwards, these cracks continued to develop along with the loading process. At the displacement of 20 mm, rebars at Sections A and F yielded and plastic hinges formed in these regions (Point a). As the load increased, plastic hinges formed at Sections C, D and G and the first peak resistance (Point b) of the specimen was reached at the displacement of 48 mm. When reaching a displacement of 50 mm, concrete crushed at the top of Section D and the bottom of Section F. Following this, concrete crushing was also observed at the bottom of Sections A and G at the displacements of 75mm and 140 mm, respectively. Along with concrete crushing, the flexural capacities of the X- and Y-beams decreased steadily, resulting in a decline in the collapse resistance (i.e., Points b to c). When the displacement reached 157 mm (Point c), the collapse resistance dropped to the minimum value (F_t). In Stage oc (from Points o to c), referring to the beam mechanism, the collapse resistance of the specimen mainly relied on the flexural capacities of the X- and Y-beams and the compressive arch action (CAA) within the X-beams.

After Point c, cracks in the X-beams developed throughout the entire cross section (Figure 9a). Then tensile cracks gradually propagated and distributed along the full length of the beams. This confirmed the axial elongation of the X-beams, indicating that all of the reinforcement in the beam was in tension and the applied load was resisted through the axial forces of the beams. Stage ce is defined as the catenary mechanism. Cracks widened as the displacement increased and the widest ones were those tensile cracks at Sections C and D. Consequently, the largest tensile strains in the reinforcement were also observed at these sections. At the displacement of 580 mm, the load reached the second peak value (Point d). Then two bottom rebars at Section C ruptured simultaneously, leading to a sudden drop in the load-displacement curve. When the loading process continued, the load increased slightly. At the displacement of 621mm, the test was terminated. The final failure mode of BE1 is shown in Figure 9. As the Y-beam had a fully fixed restraint at one end and a much weaker restraint at the other end (offered by the X-beams), the catenary effect was not obvious in the Y-beam. Accordingly, no cracks throughout the entire cross section were found in the Y-beam.

3.2 Beam-slab specimen SE1

The load-displacement curve and the final failure mode of SE1 are shown in Figure 8 and Figures 10 and 11, respectively. Firstly, flexural cracks appeared at the bottom of Sections C and D and the top of Sections A and F when the displacement reached 6 mm and 16mm, respectively. At the displacement of 24 mm, rebars at Sections A and F yielded and plastic hinges formed in these regions (Point a). Due to the slab restraint, the X-beams rotated around the X-axis when they moved downward. Under the coupled effect of bending and torsion, diagonal cracks formed in the X-beams. At the displacement of 26 mm, a 45-degree diagonal crack occurred 600 mm away from Section F. Afterwards, the tensile and diagonal cracks gradually propagated and widened. When the displacement reached 30 mm, a 45-degree diagonal crack was found at the bottom of the slab near the joint (Figures 10b and 11b). At the displacement of 52 mm, the load-displacement curve reached the peak of the beam mechanism (Point b). Then concrete crushed at the compressive zones of Sections A and F and Section G when the displacement reached 56 mm and 60 mm, respectively. The flexural capacities at the beam ends decreased and the collapse resistance of the specimen decreased accordingly. As the displacement continued to increase, the concrete at the compressive zones of Sections A, F and G crushed severely with spalling. At the same time, buckling of the compressive reinforcement was also found at the bottom of the X-beams and Y-beam (Figures 10c and 10e).

(a) The X-beams

(b) The Y-beam

Figure 10 Failure modes of SE1 ((b) to (e) upward view)

(a) Top of the slab

(b) Bottom of the slab

Figure 11 Crack distribution in the slabs in SE1

After the displacement exceeded 150 mm, the collapse resistance increased again due to the tensile membrane action of the slabs and the catenary action of the X-beams. Cracks at Sections C and D widened and the strain of rebars in these regions developed rapidly with the increase of displacement. When the displacement reached 560 mm and 595 mm, two bottom beam rebars at Section D ruptured (Figure 10d). At this time, the crack in the slab and the diagonal cracks in the X-beams merged together near Sections B and E with significantly developed crack width (see Figures 10a and 10g). The merging of cracks from the slab to the beam at Sections B and E was due to the smaller stirrup ratio at those sections (see Figure 4a). In addition, one top rebar in the beam and one bottom slab rebar at Section C close to the free edge ruptured at the displacement of 606 mm and 620 mm, respectively. When the rebars ruptured one after another, the collapse resistance of the specimen decreased significantly and the test was ended.

The failure modes of other beam-slab specimens (i.e., SE2, SE3 and SE4) were similar to those of SE1. Table 5 summarizes all the typical experimental phenomena and the corresponding vertical displacements during the collapse process of the specimens.

Table 5 Typical experimental phenomena and corresponding vertical displacements (unit: mm)

The following characteristics can be concluded from the failure modes of the beam-slab specimens: (1) The cracks were developed (see Figure 11) by the following two steps. Under the beam mechanism, only the cracks near the boundary beams on the top surface of the slab and those along the radial direction on the bottom surface of the slab would occur due to the bending deformation. These two sets of cracks ran in opposite directions because the directions of the principal tensile stresses on the top and bottom surfaces were orthogonal. However, under the catenary mechanism, the direction of the principal tensile stress on the bottom surface aligned closely to that on the top surface. This resulted in the cracks firstly appeared at 45 degree to the slab corners on the top surface to consequently propagate to the bottom surface. (2) The X-beams were in torsion due to the slab constraints, resulting in diagonal cracks in the beams. Such cracks were quite different from those observed in BE1, of which the tensile cracks were perpendicular to the beam axis. (3) Similar to BE1, cracks in the Y-beam did not extend throughout the cross section. This confirmed that the catenary mechanism was not developed in this beam. (4) The beam-slab specimens had higher tensile reinforcement ratios at Sections A, F, and G compared to BE1, leading to significantly deeper compressive zones at these sections than those of BE1. Therefore, much more severe crushing and spalling of concrete and buckling of the compressive rebars in these compressive zones were observed under the beam mechanism. (5) Under the catenary mechanism, after the rupture of bottom rebars in the X-beams, the released tensile force was carried by the rebars at the top of the X-beams and in the slabs. As a result, the specimens retained a higher collapse resistance and the displacement was allowed to continuously increase until the rebars ruptured at the top of the beams and in the slab.

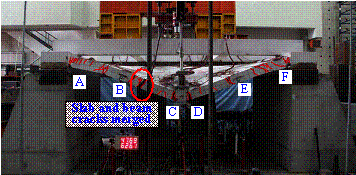
4 Collapse mechanisms of the specimens

In this section, the material strain development at Sections A to I during the entire collapse process is analyzed to explore the collapse-resistant mechanisms. In the subsequent analysis, BB and BT represent the bottom and top reinforcements in the beams, respectively; SB and ST represent the bottom and top reinforcements in the slab, respectively; CH represents the longitudinal strain of concrete at the half height of the beams. 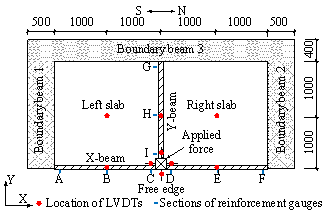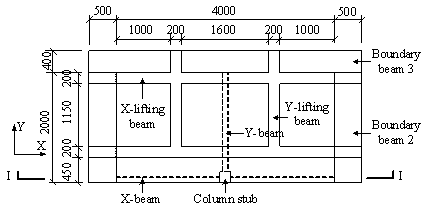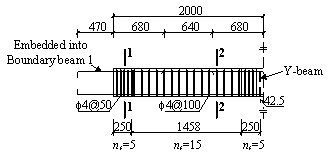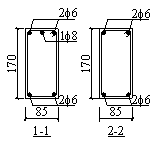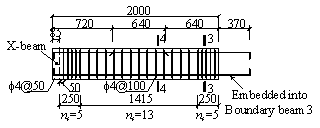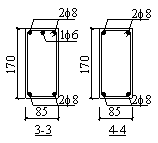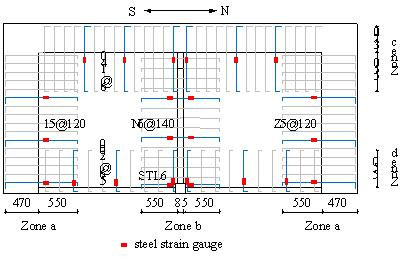The number and position of the strain gauges in the slab are shown in Figure 5. The tensile and compressive strains are defined as positive and negative, respectively, in the following analyses. 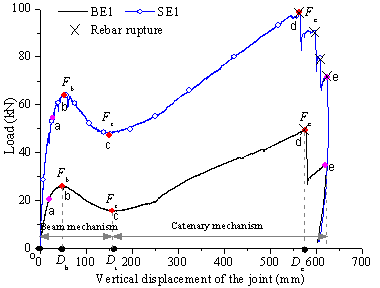To clearly illustrate the relationship between the material strain and structural resistance, the load-displacement responses of the specimens (represented by the gray lines) are also presented along with the strain development.

4.1 X-direction collapse-resistant mechanism

4.1.1 X-direction beams

The strains of beam reinforcement at Section A of BE1 and SE1 are shown in Figure 12. It can be found that under the beam mechanism: (1) Before the displacement exceeded D_b, the compressive strain of BB in SE1 was greater than that in BE1 while the tensile strain of BT was smaller. This is because the slab reinforcement was also in tension and resulted in a higher tensile reinforcement ratio at this section. (2) After the displacement exceeded D_b, the strain of BB in SE1 continued to grow until the rebar buckled due to compression. In contrast, the strain of BB in BE1 had a smaller strain and the buckling of the rebar was not observed in the test.

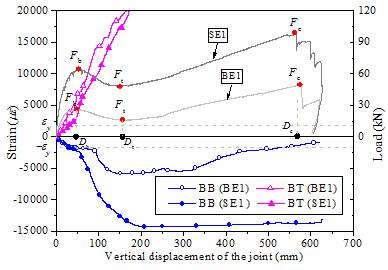
Figure 12 Reinforcement strains at Section A of BE1 and SE1

Under the beam mechanism, the compressive strain distributed throughout the height of Section B in both SE1 and BE1 (see Figure 13), which indicated the existence of the axial compressive force and confirmed the CAA in the X-beams. The compressive strains reached their maximum values near the peak point of the beam mechanism (i.e., D_b). Afterwards, the compressive strains decreased gradually and changed to tensile strains and eventually the specimens were under the catenary mechanism.

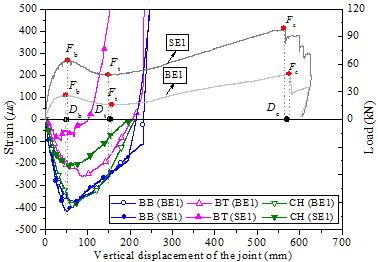
Figure 13 Reinforcement strains at Section B of BE1 and SE1

The reinforcement strains at Section C of BE1 and SE1 are shown in Figure 14. STL6 represents the strain of ST at the location as shown in Figure 5. Under the beam mechanism, BT and BB in BE1 were in compression and tension, respectively, which indicated that the height of compressive zone was greater than a_s (i.e., the distance between the center of the beam top rebars and the upper surface of the beam). In contrast, both BT and BB in SE1 were in tension and only ST was in compression, indicating that the height of compressive zone was smaller than a_s. The slab led to a larger compressive reinforcement ratio at Section C and also worked as a flange which increased the width of the concrete compressive zone. As a result, the height of compressive zone at Section C of SE1 was smaller than that of BE1. At the same time, a smaller height of the compressive zone resulted of a larger distance between the tensile reinforcement and the neutral axis, making the increase of the tensile strains of the bottom rebars in SE1 much faster than those in BE1. Under the catenary mechanism, BT in BE1 and ST in SE1 changed from compression to tension by which the entire Section C was in tension. When the load-displacement curves reached the peak point of the catenary mechanism (D_c), the beam reinforcement strains were much larger than the yield strain, indicating that the rebars in the beams contributed significantly to the collapse resistance of the specimens.

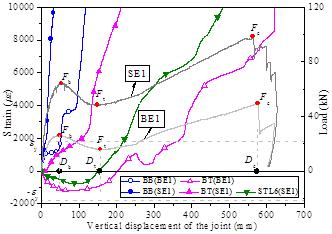
Figure 14 Reinforcement strains at Section C of BE1 and SE1

During the collapse process, the behavior of the X-beams in BE1 can be concluded as follows: (1) Under the beam mechanism, the flexural strengths of beam ends (i.e., Sections A, C, D and F) contributed considerably to the progressive collapse resistance. Significant axial forces were also developed in the beams. As a result, the CAA in the beams also contributed to the progressive collapse resistance. (2) Under the catenary mechanism, the beam ends lost their flexural strengths, the axial force transformed from compression to tension and the tensile cracks distributed throughout the entire beam. Therefore, concrete lost its bearing capacity and the external load was resisted by the continuous reinforcement in the X-beams through the catenary action.

4.1.2 X-direction slabs

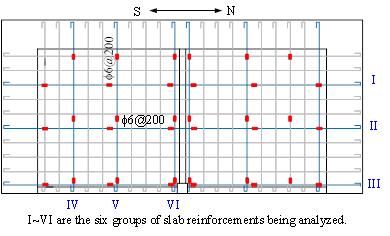
In order to further investigate the interaction of the X-beams and slabs of SE1 in resisting progressive collapse, the strains of the X-direction ST and SB at the peak displacements of the beam mechanism (i.e., D_b) and the catenary mechanism (i.e., D_c) are given in Figure 15. The locations of the six groups of slab reinforcements (i.e., Group I-VI) are given in Figure 5b. Due to symmetry, only the reinforcement strains on the south side of the slab (left slab, Figure 2) are presented herein. As the measuring range of the steel strain gauge was 20,000 me, the strain values of Group III exceeding such a measuring range are not presented in the figure. It can be seen from the figure that:

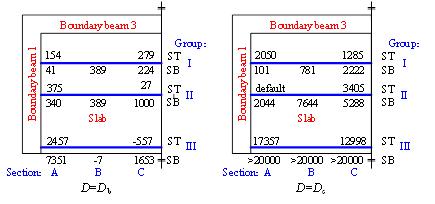
Note: ST and SB are the top and bottom reinforcement in the slab, respectively.

Figure 15 Strains of the X-direction reinforcements in the slab of SE1 (unit: me)

(1) Under the beam mechanism, ST and SB were in tension at Section A, suggesting that the compressive zone at this section was only located in the bottom area of the beams. At Section C, only the top reinforcement of Group III was in compression whilst the other reinforcement, i.e., the slab bottom reinforcement of Group III and all reinforcement of Groups I and II, were in tension. This indicates that the compressive zone at Section C was mainly located at the top of X-beam and the part of slab close to the free edge. Hence, the compressive force transferring path of CAA in the X-direction of beam-slab substructure can be illustrated as Figure 16. The force was transferred from a certain range of the top area of the slab at Section C to the bottom area of the X-beam at Section A.

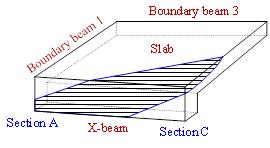
Figure 16 Compressive stress path of CAA in the beam mechanism of SE1

(2) Under the catenary mechanism, all reinforcement in the slab were in tension, among which the reinforcement within 2/3 width of the slab from the free edge yielded. The closer to the free edge, the larger the reinforcement strains were. Consequently, the portion of the slab close to the free edge contributed the most to the structural resistance under the catenary mechanism.

It can be concluded that the floor system of SE1 in the X-direction exhibited uneven deformation under the edge-column-removal scenario. This led to the contribution of the slabs to the collapse resistance, under both the beam and catenary mechanisms, mainly through the portion close to the free edge where the largest deformation occurred. 

4.2 Y-direction collapse-resistant mechanism

4.2.1 Y-direction beams

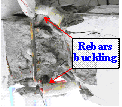
The reinforcement strains at Section G of BE1 and SE1 are shown in Figure 17. Under the beam mechanism, the typical over-reinforced failure mode was also found at this section of SE1, in which BT did not yield when BB exceeded the concrete crushing strain. This was consistent with the experimental observation that the concrete in compression seriously crushed and spalled and the bottom reinforcement buckled. Such over-reinforced failure mode is a result of the tensile reinforcement ratio being significantly increased by the Y-direction slab reinforcement. In contrast, BB of BE1 was much smaller and the beam end exhibited an under-reinforced bending mechanism. The maximum compressive strain in BB of BE1 under the beam mechanism was only 671 me. After  the maximum strain was measured, the strain gauge might be damaged because of severe concrete crushing.

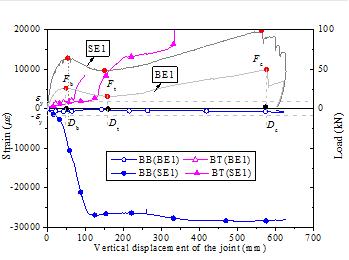
Figure 17 Reinforcement strains at Section G of BE1 and SE1

It can be found from Figure 18 that BB was in compression and BT was in tension at Section H of BE1 and SE1 under both the beam and catenary mechanisms. Such a phenomenon was different from the tension state of Section B in the X-beams under the large deformation stage, indicating that the catenary effect was not significant in Y-beam under this stage.

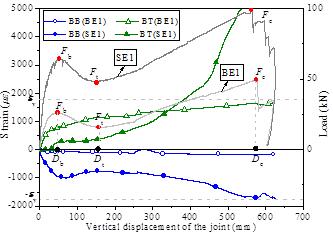
Figure 18 Reinforcement strains at Section H of BE1 and SE1

It can be seen from Figure 19 that: (1) For BE1 under the beam mechanism, BB at Section I was in tension whilst BT at Section I was in compression, indicating a positive bending moment at Section I of the Y-beam. As was mentioned before, the bending moments at Sections G and H were negative, meaning that the direction of bending deformation reversed in the middle of the Y-beam of BE1. Such a conversion was caused by the restraint at the beam end from the X-beams. 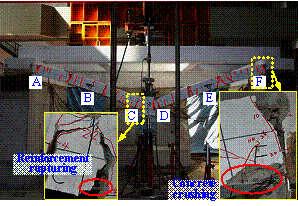The above analysis can be supported by the crack distribution of the Y-beam of BE1 (Figure 9b), where tensile cracks propagated from the beam bottom at Section I and the beam top from Sections G to H. (2) Under the catenary mechanism, BT at Section I of BE1 transformed from compression to tension. Even though the tensile strain was small, a tensile force was developed in the Y-beam under the large deformation stage. Note that the catenary action in the Y-direction was much weaker than that in the X-direction according to the magnitude of the measured strains. (3) Unlike BE1, BB in SE1 was in compression and BT was in tension at Section I, indicating that the bending moment at this section was negative. Thus, all of Sections G, H and I were under negative bending moment which was different from BE1. The torsional stiffness of the X-beams provided the flexural restraint on the Y-beam for BE1. In SE1, although the slabs enhanced the torsional stiffness of the X-beams, the slabs also induced a much larger flexural stiffness. Hence, the Y-beam and the slabs of SE1 performed like a cantilever in which the bending moment kept the same sign.

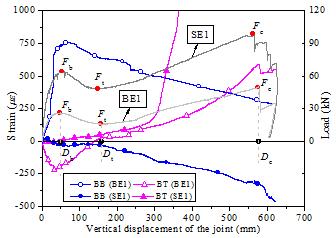
Figure 19 Reinforcement strains at Section I of BE1 and SE1

The collapse-resistant mechanism of the Y-beam of BE1 can be concluded below: (1) Under the beam mechanism, the bending moment at Section I could be neglected because the material strains at Section I were much smaller than those at Section G. Consequently, the Y-beam can be approximately treated as a cantilever with a concentrated load at the free end. (2) Under the catenary mechanism, because the residual flexural strength and the tying force of the beam reinforcement in the Y-beam were considerably smaller compared to the catenary tensile force in the X-beams, the contribution of the Y-beam to the collapse resistance can be neglected, too.

4.2.2 Y-direction slabs

The strains of the slab rebars in the Y-direction were also measured as shown in Figure 20. Due to symmetry, only the strains on the south side of the slab are presented herein. It can be seen from the figure that: (1) At the peak load of the beam mechanism, ST and SB at Section G were in tension. The closer to the Y-beam, the larger reinforcement strains were. This was because the slabs functioned as the flanges of the Y-beam under the negative bending moment. All of the reinforcement in the slab was in tension, indicating that the height of tensile zone was larger than the thickness of the slab. (2) At the peak load of the catenary mechanism, as the Y-beam was restrained by the X-beams and the slabs when they deflected downwards, ST and SB at all sections in the Y-direction were in tension. However, the reinforcement strains in the Y-direction of the slab were much smaller than those in the X-direction (see Figure 15).

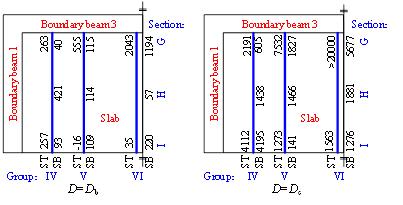
Note: ST and SB are the top and bottom reinforcement in the slab, respectively.

Figure 20 Strains of the Y-direction reinforcement in the slab of SE1 (unit: me)

It can be found that the collapse-resistant mechanisms of SE1 in the Y-direction are as follows: (1) Under the beam mechanism, the beam-slab substructure in the Y-direction performed like a cantilever in which the external load was mainly resisted by the flexural strength. The presence of the slabs led to the over-reinforced failure mode at Section G. (2) Under the catenary mechanism, the residual flexural strength and the tying force in the Y-direction of the slabs and the Y-beam were very small, therefore their contribution to the collapse resistance can be ignored.

5 Effects of various structural parameters on progressive collapse resistance

The load-displacement curves of all the specimens are presented in Figure 21. The peak values of their collapse resistances are listed in Table 6.

Table 6 Collapse resistances of the specimens

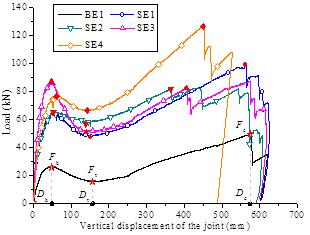
Figure 21 Load-displacement curves of all the specimens

5.1 Effect of the slab

By comparing the results of the beam-slab specimen SE1 and the beam specimen BE1, it can be found that:

(1) The presence of the slabs improved F_b by 146%. According to the above discussion, F_b mainly relied on the flexural strengths at the beam ends (i.e., Sections A, F and G and Sections C and D). At Sections A, F and G, the increased slab reinforcement improved the tensile reinforcement ratio and the ultimate flexural strengths. At Sections C and D, both the compressive reinforcement ratio and the width of the concrete compressive zone were increased, leading to a much smaller height of the compressive zone when the bottom rebars yielded. As a result, the lever-arm of the tensile force of bottom rebars increased and resulted in a larger flexural strength of these sections. Consequently, the beam-slab specimen had a higher collapse resistance under the beam mechanism.

(2) The presence of slabs increased F_c by 98%. F_c mainly relied on the axial force of the continuous reinforcement. As the deformation of the slab was unevenly distributed, only the portion of the reinforcement in the slab near the X-beams (or free edge) contributed substantial catenary forces to resist the external load. Consequently, although the amount of the continuous reinforcement in the slab was 2.5 times that in the beam, the improvement of F_c was far less than such a scale.

5.2 Effect of the slab thickness

The slab thickness of SE2 was 50% greater than SE1. To satisfy the requirement of the minimum reinforcement ratio of the slab as specified in the Chinese Code for the Design of Concrete Structures [40], the reinforcement was increased by 43% in the slab of SE2. Note that this arrangement strictly complied with the actual engineering practice. The experimental results are summarized herein:

(1) Although both the slab thickness and reinforcement were increased in SE2, F_b of SE2 remained essentially the same as that of SE1. F_b was contributed by the bending capacities of the beam ends in two directions and the compressive arch action in the X-direction only. At Sections A, F and G, over-reinforced failure occurred in which additional reinforcement in the slabs has little effect on the flexural capacity. Similarly, at Sections C and D, the additional slab reinforcement was located in either the compressive zones or the low-tensile-stress zones as discussed in Section 4.1.2 and in turn contributed little to the flexural strength. All these factors led to almost unchanged F_b of SE2 as compared to SE1.

(2) Under the catenary mechanism, F_c of SE2 was greater than that of SE1 before the rupture of the reinforcement. Although the slab reinforcement in SE2 was 43% larger than that in SE1, at the same vertical displacement of 366 mm, the bearing capacity of SE2 was 81 kN, which was only 13% greater than that of SE1 (i.e., 72 kN). Due to the unevenly distributed reinforcement strains in the slab, only the portion of the X-direction reinforcement in the slab close to the free edge contributed significant catenary forces to resist the external load.

5.3 Effect of the beam height

The beam height of SE3 was 18% higher than that of SE1. The amount of reinforcement in these two specimens remained the same. As the beam height increased, the heights of the compressive zones and the lever-arms of the tensile and compressive resultants increased at all beam ends. In consequence, F_b of SE3 was 36% greater than SE1 under the beam mechanism. Under the catenary mechanism, the collapse resistance of SE3 was slightly higher than that of SE1. This is because, under the same vertical displacement, the strain of SB in SE3 was slightly larger than that in SE1 due to a larger beam height. Note that SE3 had a larger resistance of the catenary action than SE1 at the same displacement when D > D_t (see Figure 21). However, a reinforcing steel bar in SE3 was found to occasionally rupture leading to a smaller resistance under the catenary action when the test was terminated.

5.4 Effect of the seismic design intensity

The design seismic intensity of SE4 was much higher than that of SE1 according to the Chinese Code for Seismic Design of Buildings [41]. The PGA of the design earthquake was increased from 0.05g (SE1) to 0.20g (SE4). The increase in the seismic design intensity resulted in an increase of the amount of seismic reinforcement in the beam. In contrast, the slab reinforcement remained the same. It can be found from the experimental results that:

(1) The tensile reinforcement ratio at Section A was increased by 116% (from 0.77% for SE1 to 1.69% for SE4). However, due to the over-reinforced failure at Sections A, F and G, the additional tensile reinforcement had limited effect on the flexural strength. In contrast, the additional bottom reinforcement in X-beams at Sections C and D can effectively improve the flexural strength at these sections. In consequence, the resistance of SE4 was 19% higher than that of SE1. The resistance was improved more significantly than that by increasing the slab reinforcement.

(2) Under the catenary mechanism, F_c of SE4 was significantly higher than that of SE1 at the same vertical displacement. When the displacement reached 453 mm, F_c of SE4 and SE1 were 125 kN and 84 kN, respectively. F_c mainly relied on the catenary force from the X-direction reinforcement in the X-beams and the slabs. Note that the area of the longitudinal reinforcement in the X-beams of SE4 was 2.78 times that of SE1. Meanwhile, F_c of SE4 only increased by 49% comparing to SE1. This is because the top reinforcement in the slab near the X-beams also contributed to F_c, and reduced the effect of change in the beam reinforcement.

6 Conclusion

In order to investigate the progressive collapse resistance of RC beam-slab substructures under an edge-column-removal scenario, five 1/3-scaled edge-span substructure specimens, including four beam-slab specimens and one beam specimen without a slab, were designed and tested in this study. The effects of beam height, slab thickness and seismic reinforcement were considered. Systematic analyses on the collapse mechanisms and the collapse resistance of the specimens were conducted based on the experimental results. The main conclusions are:

(1) Under the beam mechanism, the collapse resistance was mainly contributed by the flexural strengths in both X- and Y-directions and CAA in the X-direction of the beam-slab substructure. Under the catenary mechanism, the progressive collapse resistance was largely provided by the catenary tensile force in the longitudinal reinforcement of the beams and slabs. Because of the boundary restraints and the unevenly distributed deformation, only the X-beams and the slab reinforcement close to the free edge contributed significantly to the progressive collapse resistance.

(2) The presence of the slabs significantly enhanced the progressive collapse resistance of the beam-slab substructures under an edge-column-removal scenario. Under the beam mechanism and the catenary mechanism, respectively, the resistances of the control beam-slab specimen were increased by 146% and 98% compared to those of the beam specimen.

(3) The higher seismic design intensity leaded to the increase of the beam reinforcement exhibiting large deformation which consequently resulted in a much larger collapse resistance under both beam and catenary mechanism. The increase of the beam height effectively improved the progressive collapse resistance under the beam mechanism but had limited impact to that under the catenary mechanism. In contrast, increasing the slab reinforcement marginally improved the collapse resistance under the catenary mechanism but contributed little to that under the beam mechanism.

Acknowledgment

The authors are grateful for the financial support received from.

Reference

[1]      American Society of Civil Engineers (ASCE). Minimum design loads for buildings and other     structures (ASCE7-10). Reston (VA); 2010.

[2]      Corley WG, Sosen MA, Thornton CH, Mlakar PF. The Oklahoma City bombing: improving building performance through multi-hazard mitigation (FEMA 277). Washington (DC): FEMA/ASCE; 1996.

[3]      European Committee for Standardization. EN 1991-1-7: Eurocode 1: Actions on structures, part 1-7: general actions-accidental actions. Brussels (Belgium); 2006.

[4]      British Standard Institute. BS8110: Structural use of concrete, part 1: code of practice for design and construction. United Kingdom; 1997.

[5]      Department of Defense (DoD). Unified facilities criteria (UFC): design of structures to resist progressive collapse. Washington (DC); 2010.

[6]      General Service Administration (GSA). Alternate path analysis & design guidelines for progressive collapse resistance. Washington (DC); 2013.

[7]      Choi H, Kim J. Progressive collapse-resisting capacity of RC beam-column sub-assemblage. Mag Concr Res 2011; 63(4):297-310. doi: 10.1680/macr.9.00170

[8]      Yap LS, Li B. Experimental investigation of reinforced concrete exterior beam-column subassemblages for progressive collapse. ACI Struct J 2011; 108(5): 542-52. doi: 10.14359/51683211

[9]      Helmy H, Salem H, Mourad S. Progressive collapse assessment of framed reinforced concrete structures according to UFC guidelines for alternative path method. Eng Struct 2012; 42: 127-41. doi: 10.1016/j.engstruct.2012.03.058

[10]  Ren PQ, Li Y, Guan H, Lu XZ. Progressive collapse resistance of two typical high-rise RC frame shear wall structures. J Perform Constr Facil 2015; 29(3): 04014087. doi: 10.1061/(ASCE)CF.1943-5509.0000593

[11]  Bao Y, Kunnath SK. Simplified progressive collapse simulation of RC frame-wall structures. Eng Struct 2010; 32(10): 3153-62. doi: 10.1016/j.engstruct.2010.06.003

[12]  Qian K, Li B. Experimental study of drop-panel effects on response of reinforced concrete flat slabs after loss of corner column. ACI Struct J 2013; 110(2): 319-29. doi: 10.14359/51684411

[13]  Yi W, Zhang F, Kunnath SK. Progressive collapse performance of RC flat plate frame structures. J Struct Eng 2014; 140: 040140489. doi: 10.1061/(ASCE)ST.1943-541X.0000963

[14]  Keyvani L, Sasani M, Mirzaei Y. Compressive membrane action in progressive collapse resistance of RC flat plates. Eng Struct 2014; 59(2): 554-64. doi: 10.1016/j.engstruct.2013.10.040

[15]  Liu J, Tian Y, Orton S, Said A. Resistance of flat-plate buildings against progressive collapse. I: modeling of slab-column connections." J Struct Eng 2015; 141(12): 04015053. doi: 10.1061/(ASCE)ST.1943-541X.0001294

[16]  Liu J, Tian Y, Orton S. Resistance of flat-plate buildings against progressive collapse. II: system response. J Struct Eng 2015; 141(12): 04015054. doi: 10.1061/(ASCE)ST.1943-541X.0001295

[17]  Sagiroglu1 S, Sasani M. Progressive collapse-resisting mechanisms of reinforced concrete structures and effects of initial damage locations. J Struct Eng 2014; 140(3): 04013073. doi: 10.1061/(ASCE)ST.1943-541X.0000854

[18]  Qian K, Li B, Ma JX. Load-carrying mechanism to resist progressive collapse of RC buildings. J Struct Eng 2014; 141(2): 04014107. doi: 10.1061/(ASCE)ST.1943-541X.0001046

[19]   Li Y, Lu XZ, Guan H, Ren PQ. Numerical investigation of progressive collapse resistance of RC frames subject to column removals from different stories. Adv Struct Eng 2016; 19(2): 314-26. doi: 10.1177/1369433215624515 

[20]  Tsai MH, Lin BH. Investigation of progressive collapse resistance and inelastic response for an earthquake-resistant RC building subjected to column failure. Eng Struct 2008; 30(12): 3619-28. doi: 10.1016/j.engstruct.2008.05.031

[21]  Li Y, Lu XZ, Guan H, Ye LP. An energy-based assessment on dynamic amplification factor for linear static analysis in progressive collapse design of ductile RC frame structures. Adv Struct Eng 2014; 17(8): 1217-25. doi: 10.1260/1369-4332.17.8.1217

[22]  Li Y, Lu XZ, Guan H, Ye LP. Progressive collapse resistance demand of RC frames under catenary mechanism. ACI Struct J 2014; 111(5): 1225-34. doi: 10.14359/51687029

[23]  Li Y, Lu XZ, Guan H, Ren PQ, Qian LP. Probability-based progressive collapse-resistant assessment for reinforced concrete frame structures. Adv Struct Eng 2016; (Accepted). doi: 10.1177/1369433216649385.

[24]  Li Y, Lu XZ, Guan H, Ying MJ, Yan WM. A case study on a fire-induced collapse accident of a reinforced concrete frame-supported masonry structure. Fire Tech 2016; 52(3): 707-29. doi: 10.1007/s10694-015-0491-0

[25]  Lu XZ, Li Y, Guan H, Ying MJ. Progressive collapse analysis of a typical super-tall reinforced concrete frame-core tube building exposed to extreme fires. Fire Tech 2016; (Accepted) doi: 10.1007/s10694-016-0566-6

[26]  Xu G, Ellingwood BR. An energy-based partial pushdown analysis procedure for assessment of disproportionate collapse potential. J Constr Steel Res 2011; 67(3): 547-55. doi: 10.1016/j.jcsr.2010.09.001

[27]  Izzuddin BA, Vlassis AG, Elghazouli AY, Nethercot DA. Progressive collapse of multi-storey buildings due to sudden column loss-part I: simplified assessment framework. Eng Struct 2008; 30(5): 1308-18. doi: 10.1016/j.engstruct.2007.07.011

[28]  Li Y, Lu XZ, Guan H, Ye LP. An improved tie force method for progressive collapse resistance design of reinforced concrete frame structures. Eng Struct 2011; 33(10): 2931-42. doi: 10.1016/j.engstruct.2011.06.017

[29]  Su YP, Tian Y, Song X. Progressive collapse resistance of axially-restrained frame beams. ACI Struct J 2009; 106(5): 600-7. doi: 10.14359/51663100

[30]  Yi WJ, He QF, Xiao Y, Kunnath SK. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures. ACI Struct J 2008; 105(4): 433-9. doi: 10.14359/19857

[31]  Sadek F, Main JA, Lew HS, Bao Y. Testing and analysis of steel and concrete beam-column assemblies under a column removal scenario. J Struct Eng 2011; 137(9): 881¨C92. doi: 10.1061/(ASCE)ST.1943-541X.0000422

[32]  Yu J, Tan KH. Experimental and numerical investigation on progressive collapse resistance of reinforced concrete beam column sub-assemblages. Eng Struct 2013; 55(10): 90-106. doi: 10.1016/j.engstruct.2011.08.040

[33]  Sasani M, Werner A, Kazemi A. Bar rupture modeling in progressive collapse analysis of reinforced concrete structures. Eng Struct 2011; 33(2): 401-9. doi: 10.1016/j.engstruct.2010.10.023

[34]  Qian K, Li B. Slab effects on response of reinforced concrete substructures after loss of corner column. ACI Struct J 2012; 109(6): 845-55

[35]  Ren PQ, Li Y, Lu XZ, Guan H, Zhou YL. Experimental investigation of progressive collapse resistance of one-way reinforced concrete beam-slab substructures under a middle-column-removal scenario, Eng Struct 2016; 118: 28-40. doi: 10.1016/j.engstruct.2016.03.051

[36]  Prasad S, Hutchinson TC. Evaluation of older reinforced concrete floor slabs under corner support failure. ACI Struct J 2014; 111(4): 839-49. doi: 10.14359/51686735

[37]  Xiao Y, Kunnath S, Li FW, Zhao YB, Lew HS, Bao Y. Collapse test of three-story half-scale reinforced concrete frame building. ACI Struct J 2015; 112(4): 429-438. doi: 10.14359/51687746

[38]  Pham XD, Tan KH. Experimental response of beam-slab substructures subject to penultimate-external column removal. J Struct Eng 2015; 141(7): 04014170. doi: 10.1061/(ASCE)ST.1943-541X.0001123

[39]  Qian K, Li B, Zhang Z. Influence of multicolumn removal on the behavior of RC floors. J Struct Eng 2016; 142(5): 04016006. doi: 10.1061/(ASCE)ST.1943-541X.0001461

[40]  Ministry of Housing and Urban-Rural Development of the People¡¯s Republic of China (MOHURD). Code for design of concrete structures. GB50010-2010, Beijing, China; 2010.

[41]  Ministry of Housing and Urban-Rural Development of the People¡¯s Republic of China (MOHURD). Code for seismic design of buildings. GB50011-2010, Beijing, China; 2010.

tables and figures

List of Tables

Table 1.                     Dimensions of the prototype structure and the scaled specimen (unit: mm)

Table 2.                     Sectional dimensions and beam reinforcements in the specimens (unit: mm)

Table 3.                     Slab reinforcements in the specimens (unit: mm)

Table 4.                     Material properties of the rebars

Table 5.                     Typical experimental phenomena and corresponding vertical displacements (unit: mm)

Table 6.                     Collapse resistances of the specimens

List of Figures

Figure 1.                   Layout of the six-story RC frame (unit: m)

Figure 2.                   Test area of the substructure (unit: mm)

Figure 3.                   Detailed dimensions of SE1 (unit: mm)

Figure 4.                   Reinforcements in the beams of SE1 (unit: mm)

Figure 5.                   Reinforcements in the slabs of SE1 (unit: mm)

Figure 6.                   Boundary conditions applied in the tests

Figure 7.                   One-way hinge on top of the column stub

Figure 8.                   Load-displacement curves of BE1 and SE1

Figure 9.                   Failure modes of BE1

Figure 10.               Failure modes of SE1

Figure 11.               Crack distribution in the slabs in SE1

Figure 12.               Reinforcement strains at Section A of BE1 and SE1

Figure 13.               Reinforcement strains at Section B of BE1 and SE1

Figure 14.               Reinforcement strains at Section C of BE1 and SE1

Figure 15.               Strains of the X-direction reinforcements in the slab of SE1 (unit: me)

Figure 16.               Force transferring path of CAA in the beam mechanism of SE1

Figure 17.               Reinforcement strains at Section G of BE1 and SE1

Figure 18.               Reinforcement strains at Section H of BE1 and SE1

Figure 19.               Reinforcement strains at Section I of BE1 and SE1

Figure 20.               Strains of the Y-direction reinforcement in the slab of SE1 (unit: me)

Figure 21.               Load-displacement curves of all the specimens