References
ACI [2011] “Building code requirements for structural concrete
and commentary (ACI 318-11/318R-11),” American Concrete Institute, Farmington
Hills, Michigan.
ASCE [2010] “Minimum design loads for buildings and other
structures (ASCE/SEI 7-10),” American Society of Civil Engineers, Reston, Virginia.
ATC [1985] “Earthquake damage evaluation data for California
(ATC-13),” Applied Technology Council, Redwood, California.
Avşar, Ö., Bayhan, B. and Yakut, A. [2014] “Effective
flexural rigidities for ordinary reinforced concrete columns and beams,” The
Structural Design of Tall and Special Buildings, 23(6), 463-482.
Bommer, J. J., and Acevedo, A. B. [2004] “The use of real
earthquake accelerograms as input to dynamic analysis,” Journal of Earthquake
Engineering, 8(sup1), 43-91.
CEA [2014] “Seismic intensity map of M6.5 Ludian Earthquake
in Yunnan,” China Earthquake Administration http,//www.cea.gov.cn/publish/dizhenj/464/478/20140807085249557322083/index.html,
released on August 7, 2014.
DeBock, D. J. and Liel, A. B. [2015] “A comparative evaluation
of probabilistic regional seismic loss assessment methods using scenario case
studies,” Journal of Earthquake Engineering, 19(6), 905-937.
Fang, L. [2009] “Experimental research on seismic shear
strength and seismic behavior of autoclaved fly ash brick wall,” Master thesis,
Changsha University of Science & Technology, Changsha, China.
FEMA [2012a] “Multi-hazard loss estimation methodology-earthquake
model. HAZUS-MH 2.1 Technical Manual,” Federal Emergency Management Agency,
Washington, DC.
FEMA [2012b] “Seismic Performance Assessment of Buildings.
Volume 1 Methodology (FEMA-P58),” Federal Emergency Management Agency, Washington,
DC.
GAQSIQ [2009] “Classification of earthquake damage to buildings
and special structures (GB/T 24335-2009),” General Administration of Quality
Supervision, Inspection and Quarantine of the People’s Republic of China, Beijing,
China.
Gasparini, D. and Vanmarcke E. H. [1976] “SIMQKE, A program
for artificial motion generation,” Department of Civil Engineering, Massachusetts
Institute of Technology, Cambridge, MA.
Gong, Y. N. [2008] “Experimental research on the seismic
performance of concrete perforated brick shear wall,” Master thesis, Zhengzhou
University, Zhengzhou, China.
Gu, X. L., Chen, G. L., Ma, J. Y. and Li, X. [2010] “Experimental
study on mechanical behavior of concrete perforated brick walls under cyclic
loading,” Journal of Building Structures, 31(12), 123-131.
Guo, Z. G., Wu, C. W., Sun, W.M. and Ni, T. Y. [2014] “Seismic
behavior of recycled concrete perforated brick masonry,” Journal of Basic
Science and Engineering, 22(3), 539-547.
Han, C. [2009] “Experimental research on the behavior of
brick masonry column and the seismic behavior of autoclaved fly ash brick,”
Master thesis, Xi’an University of Architecture and Technology, Xi’an, China.
Hori, M. [2010] Introduction to computational earthquake
engineering (2rd edition), Imperial College Press, London.
Huang, Y. H. and Wang, Q. F. [2009] “Research on shear
capacity for brick masonry strengthened by FRP,” Journal of Architecture
and Civil Engineering, 26(1), 12-18.
Lei, M. [2013] “Study on seismic behavior of row lock wall
and row lock wall strengthened with HPFL” Ph.D thesis, Hunan University, Changsha,
China.
Li, G. Q. [2006] “R-µ principle in seismic design
and overstrength character analysis of typical reinforced concrete frame structures,”
Master thesis, Chongqing University, Chongqing, China.
Li, B. D. and Wang, X. X. [2009] “Experimental research
on aseismatic performance of concrete common brick wall,” Journal of Wuhan
University of Technology, 31(16), 72-76.
Li, L. [2013] “Overstrength character and its influencing
factors research of reinforced concrete frame structures,” Master thesis, South
China University of Technology, Guangzhou, China.
Lin, S. B., Xie, L. L., Gong, M. S. and Li, M. [2010] “Performance-based
methodology for assessing seismic vulnerability and capacity of buildings,”
Earthquake Engineering and Engineering Vibration, 9(2), 157-165.
Lin, X., Zhang, H., Chen, H., Chen, H. and Lin, J. [2015]
“Field investigation on severely damaged aseismic buildings in 2014 Ludian Earthquake,”
Earthquake Engineering and Engineering Vibration, 14(1), 169-176.
Liu, L. H. [2006] “Preliminary analysis of R-µ relationships
of MDOF and influence of the degree of statical indeterminacy on overstrength,”
Master thesis, Chongqing University, Chongqing, China.
Liu, Y., Xu, Y. F. and Zhang, H. [2011] “Experimental study
on mechanical behavior of fly ash block walls restricted by constructional columns
and top beam,” Industrial Construction, 41(8), 38-41.
Lu, X.
Z., Ye, L. P., Ma, Y. H. and Tang, D. Y. [2012] “Lessons from the collapse
of typical RC frames in Xuankou School during the great Wenchuan earthquake,”
Advances in Structural Engineering, 15(1), 139-153.
Lu,
X. Z., Han, B., Hori, M., Xiong, C. and Xu, Z. [2014] “A coarse-grained
parallel approach for seismic damage simulations of urban areas based
on refined models and GPU/CPU cooperative computing,” Advances in Engineering
Software, 70, 90-103.
MAE [2006] “Earthquake risk assessment using MAEviz 2.0,
a tutorial” Mid-America Earthquake Center, University of Illinois at Urbana-Champaign,
Urbana-Champaign, Illinois.
Miao, Q. S., He, X. L., Zhou, B. Z., Liu, T. C., Wang,
Z. P. and Gu, T. Z. [2000] “Experimental study on aseismic behavior of nine-story
masonry building with small-size hollow concrete blocks,” Journal of Building
Structures, 21(4), 13-21.
Miyakoshi, J., Hayashi, Y., Tamura, K. and Fukuwa, N. [1997]
“Damage ratio functions of buildings using damage data of the 1995 Hyogo-Ken
Nanbu earthquake,” 7th International Conference on Structural Safety and Reliability
(ICOSSAR 97), 1, 349-354, Kyoto, Japan.
MOHURD [2005] “Code for design of civil buildings (GB50352-2005),”
Ministry of Housing and Urban-Rural Development of the People’s Republic of
China, Beijing, China.
MOHURD [2010a] “Code for seismic design of buildings (GB50011-2010),”
Ministry of Housing and Urban-Rural Development of the People’s Republic of
China, Beijing, China.
MOHURD [2010b] “Code for design of concrete structures
(GB 50010-2010), Ministry of Housing and Urban-Rural Development of the People’s
Republic of China, Beijing, China.
MOHURD [2012] “Load code for design of building structures
(GB 50009-2012),” Ministry of Housing and Urban-Rural Development of the People’s
Republic of China, Beijing, China.
Özhendekci, D. and Özhendekci, N. [2012] “Seismic
performance of steel special moment resisting frames with different span arrangements,”
Journal of Constructional Steel Research, 72, 51-60.
Remo, J. W. and Pinter, N. [2012] “Hazus-MH earthquake
modeling in the central USA,” Natural Hazards, 63(2), 1055-1081.
Shi, Q. X. and Yi, W. Z. [2000] “Tentative studies on the
aseismic behavior and investigation of collapse resistant capacity of porous
masonry walls,” Journal of Xi’an University of Architecture & Technology,
32(3), 271-275.
Shi,
W., Lu, X. Z. and Ye, L. P. [2012] “Uniform-risk-targeted seismic design
for collapse safety of building structures,” Science China Technological
Sciences, 55(6), 1481-1488.
Shi,
W., Lu, X. Z., Guan, H. and Ye, L. P. [2014] “Development of seismic collapse
capacity spectra and parametric study,” Advances in Structural Engineering,
17(9), 1241-1256. doi, 10.1260/1369-4332.17.9.1241
Sobhaninejad, G., Hori, M. and Kabeyasawa, T. [2011] “Enhancing
integrated earthquake simulation with high performance computing,” Advances
in Engineering Software, 42(5), 286-292.
Song, S. Y. and Ye, L. P. [2007] “A comparison of design
methods for flexure strength of RC beams between Chinese and American design
codes for RC structures,” Building Science, 23(7), 28-33.
Tantala, M. W., Nordenson, G. J., Deodatis, G. and Jacob,
K. [2008] “Earthquake loss estimation for the New York City metropolitan region,”
Soil Dynamics and Earthquake Engineering, 28(10), 812-835.
Tran, C. and Li, B. [2012] “Initial stiffness of reinforced
concrete columns with moderate aspect ratios,” Advances in Structural Engineering,
15(2), 265-276.
Trifunac, M. D. and Todorovska, M. I. [1997] “Northridge,
California, earthquake of 1994, density of red-tagged buildings versus peak
horizontal velocity and intensity of shaking,” Soil Dynamics and Earthquake
Engineering, 16(3), 209-222.
Vamvatsikos, D. and Cornell, C. A. [2005] “Direct estimation
of seismic demand and capacity of multi-degree-of-freedom systems through incremental
dynamic analysis of single degree of freedom approximation 1,” Journal of
Structural Engineering, 131(4), 589-599.
Wang, Z. G., Zha, Z. X., and Nie, J. G. [2002] “Experimental
study on antiseismic behavior of a full scale building of 6-story porous brick
and small-size hollow concrete block structure with constructional column-beam
system,” Earthquake Engineering and Engineering Vibration, 22(4),
90-96.
Wang, Z. G., Xue, G. Y., Gao, B. L. and Zhang, J. T. [2003]
“Experimental research on the seismic behavior of confined shale brick masonry
walls,” Journal of Southeast University, 33(5), 638-642.
Wang, Z. [2008] “A preliminary report on the Great Wenchuan
Earthquake,” Earthquake Engineering and Engineering Vibration, 7(2),
225-234.
Weng, X. P. [2010] “Numerical simulation analysis and experimental
study on seismic behavior of cavity wall masonry,” Master thesis, Zhejiang University,
Hangzhou, China.
Wu, H., Zhao, S. C., Xu, H., Zhang, P. B. and Wu, G. [2012]
“Damage characteristic analysis of transverse wall of brick concrete masonry
school buildings with different structural measures,” Building Structure,
42(S1), 226-230.
Wu, W. B. [2012] “Study on seismic performance of autoclaved
fly ash bricks,” Master thesis, Institute of Engineering Mechanics, China Earthquake
Administration, Harbin, China.
Xiao, J. Z., Huang, J. D. and Yao, Y. [2012] “Test on seismic
behavior of recycled concrete block walls,” Journal of Building Structures,
42(4), 100-109.
Xie,
L. L., Lu, X. Z., Guan, H. and Lu, X. [2015] “Experimental study and numerical
model calibration for earthquake-induced collapse of RC frames with emphasis
on key columns, joints and the overall structure,” Journal of Earthquake
Engineering, 19(8), 1320-1344. doi, 10.1080/13632469.2015.1040897
Xiong,
C., Lu, X. Z., Hori, M., Guan, H. and Xu, Z. [2015] “Building seismic
response and visualization using 3D urban polygonal modeling,” Automation
in Construction, 55, 25-334.
Xu,
Z., Lu, X. Z., Guan, H., Han, B. and Ren, A. Z. [2014] “Seismic damage
simulation in urban areas based on a high-fidelity structural model and
a physics engine,” Natural Hazards, 71, 1679-1693. doi,
10.1007/s11069-013-0972-8.
Xu,
Z., Lu, X. Z., Guan, H., Tian, Y. and Ren, A. Z. [2016] “Simulation of
earthquake-induced hazards of falling exterior non-structural components
and its application to emergency shelter design”, Natural Hazards,
80(2), 935-950.
Yamashita, T., Hori, M. and Kajiwara, K. [2011] “Petascale
computation for earthquake engineering,” Computing in Science & Engineering,
13(4), 44-49.
Yang, D. J., Gao, Y. F., Sun, J. B., Wang, S. X. and Cheng,
Q.X. [2000] “Experimental study on aseismic behavior of concrete block walls
with construction-core column system,” Journal of Building Structures,
21(4), 22-27.
Yang, W. J., Chen, L. Q. and Zhu, X. Q. [2008] “Experimental
study on seismic behavior of concrete perforated brick walls,” Engineering
Mechanics, 25(9), 126-133.
Yang, Y. X. [2008] “Experimental study on seismic performance
of autoclaved fly ash-lime solid brick walls,” Master thesis, Chongqing University,
Chongqing, China.
Ye, Y. H., Li, L. Q., Sun, W. M., Gu, Z. and Cheng, J.
G. [2004] “Experimental study on seismic behaviors of hollow block wall filled
with foaming concrete,” Earthquake Engineering and Engineering Vibration,
24(5), 154-158.
Yin, Z. Q. [1991] “A study for predicting earthquake disaster
loss,” Earthquake Engineering and Engineering Vibration, 11(4),
87-96.
Yin, Z. Q. [1996] “Classification of structure vulnerability
and evaluation earthquake damage from future earthquake,” Earthquake Research
in China, 12(1), 49-55.
Yin, Z. Q., Zhao, Z. and Yang, S. W. [2003] “Relation between
vulnerability of buildings and earthquake acceleration spectra (1),” Earthquake
Engineering and Engineering Vibration, 23(4), 195-200.
Yu, J. G. [2003] “Study on lateral bearing capacity and
lateral stiffness of prestressed brick walls,” Master thesis, Chongqing University,
Chongqing, China.
Zhai, C. H. and Xie, L. L. [2007] “Study on overstrength
of RC frame structures,” Journal of Building Structures, 28(1),
101-106.
Zhang, H. [2005] “Experimental study on seismic and crack-resistance
behavior of composite concrete block masonry walls,” Master thesis, Nanjing
University of Technology, Nanjing, China.
Zhang, W. [2007a] “The finite element analysis of experimental
results of and research to shear capacity of CFRP strengthened masonry,” Ph.D.
thesis, Wuhan University of Technology, Wuhan, China.
Zhang, H. [2007b] “Experimental study on seismic behavior
of load bearing walls with opening built by fly ash-autoclaved bricks and fly
ash block walls restricted by constructional columns and top-beam,” Master thesis,
Yangzhou University, Yangzhou, China.
Zhang, L. H. [2009] “Analysis on overstrength factors of
reinforced concrete frame structures,” Master thesis, Chongqing University,
Chongqing, China.
Zhang, Z. [2010] “Experimental research a theoretical analysis
on seismic behavior of masonry strengthened by SGFRP,” Ph.D. thesis, Wuhan University
of Technology, Wuhan, China.
Zhang, Y. Q. [2014] “Seismic damage analyses of masonry
structure retrofitted by prefabricated reinforced concrete panels,” Master thesis,
Institute of Engineering Mechanics, China Earthquake Administration, Harbin,
China.
Zhao, Z. Z. [1993] “Model test and nonlinear analysis of
multi-story large-bay residential structural system with less internal longitudinal
walls,” Master thesis, Tsinghua University, Beijing, China.
Zhao, F. L. [2008] “Research on overstrength factors of
reinforced-concrete frame structures,” Master thesis, Xi’an University of Architecture
and Technology, Xi’an, China.
Zhao, C. W., Shang, Y. M., Zhou, K. and Qiao, H. [2010]
“Experimental study on the seismic behavior autoclaved fly ash brick walls,”
Journal of Shenyang Jianzhu University (Natural Science), 25(1),
57-61.
Zheng, N. N. [2010] “Research on seismic behavior of masonry
structures with fabricated tie-columns,” Ph.D. thesis, Chongqing University,
Chongqing, China.
Zheng, Q. [2012] “The experimental study on the model of
anti-seismic performance and shear-carrying capacity of FRP intensified masonry
wall,” Master thesis, Shenyang Jianzhu University, Shenyang, China.
Zhou, B. Z., Zheng, W., Guan, Q. X., Liu, T. C., He, X.
L. and Wang, Z. P. [2000] “Experimental study on aseismic behavior of six-story
masonry building with small-size hollow concrete blocks,” Journal of Building
Structures, 21(4), 2-12.
Zhou, H. Y. [2004] “Experimental study on seismic behavior
of small concrete hollow block walls restricted by constructional columns,”
Master thesis, Beijing University of Technology, Beijing, China.
Zhou, X. and Zhou, D. Y. [2005] “Experimental analysis
of 3-story RC frame structures under cyclic load reversals,” Sichuan Building
Science, 31(2), 7-11.
Zhou, Y., Shi, W. X. and Han, R. L. [2012] “Vibration test and analysis of the fundamental period of
multi-story masonry structures with large-bay,” Engineering Mechanics,
29(11), 197-204.
Address to correspondence
to Xinzheng Lu, Department of Civil Engineering, Tsinghua University, Beijing,
P.R. China. E-mail: luxz@tsinghua.edu.cn
|
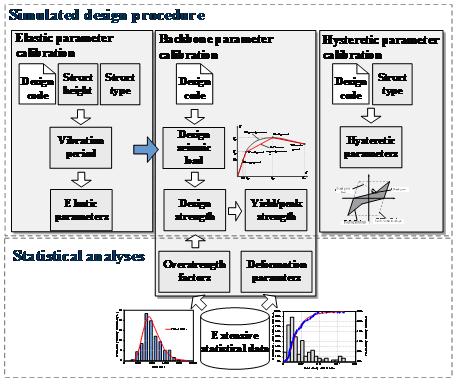
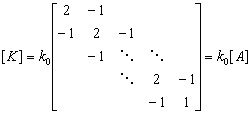 (1)
(1)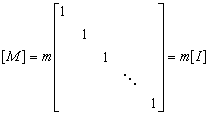 (2)
(2)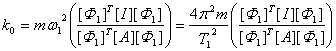 (4)
(4)